链表

发表于 更新于 分类于 ， ， 本文字数： 6.7k 阅读时长 ≈ 24 分钟 阅读次数：

相似解法题目多元组

  • 双指针：< BM5 合并 k 个已排序的链表，BM6 判断链表中是否有环， BM7 链表中环的入口点，BM8 链表中倒数最后 k 个节点，BM9 删除链表的倒数第 n 个节点，BM10 两个链表的第一个公共节点，BM13 判断一个链表是否为回文结构，BM14 链表的奇偶重排>

  • 环：< BM6 判断链表中是否有环, BM7 链表中环的入口点 >

  • 双指针定位倒数节点：< BM8 链表中倒数最后 k 个节点, BM9 删除链表的倒数第 n 个节点 >

  • 反转链表：< BM1 反转链表, BM11 链表相加(二)>

  • 归并排序：< BM5 合并 k 个已排序的链表，BM12 单链表的排序，BM20 数组中的逆序对 >

BM5 合并 k 个已排序的链表

描述

合并 k 个升序的链表并将结果作为一个升序的链表返回其头节点。

F1：归并排序

思路
  • 双指针、归并排序、分治
步骤
  1. 从链表数组的首和尾开始，每次划分从中间开始划分，划分成两半，得到左边 n/2 个链表和右边 n/2 个链表。
  2. 继续不断递归划分，直到每部分链表数为 1。
  3. 将划分好的相邻两部分链表，按照两个有序链表合并的方式合并，合并好的两部分继续向上合并，直到最终合并成一个链表。
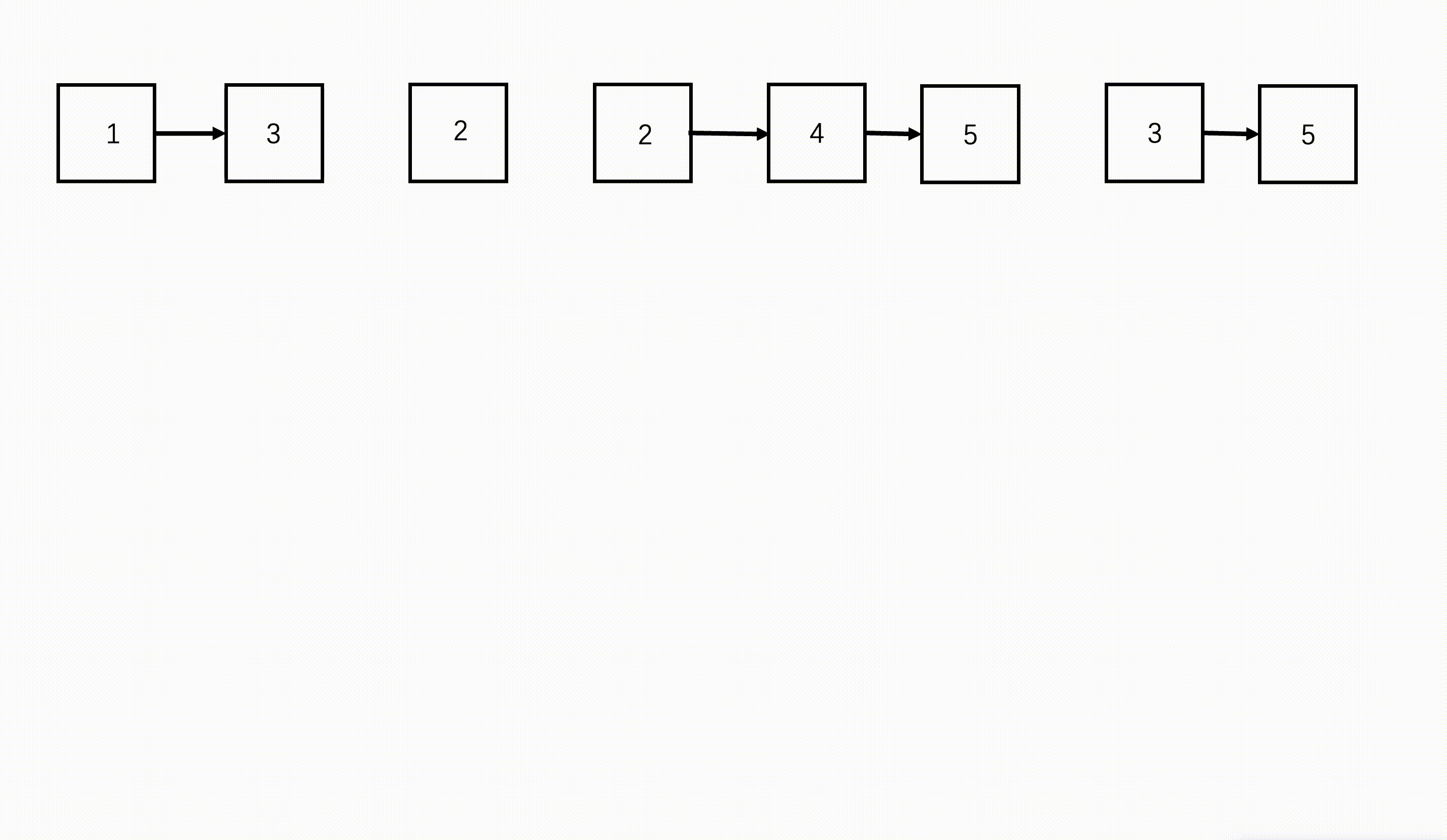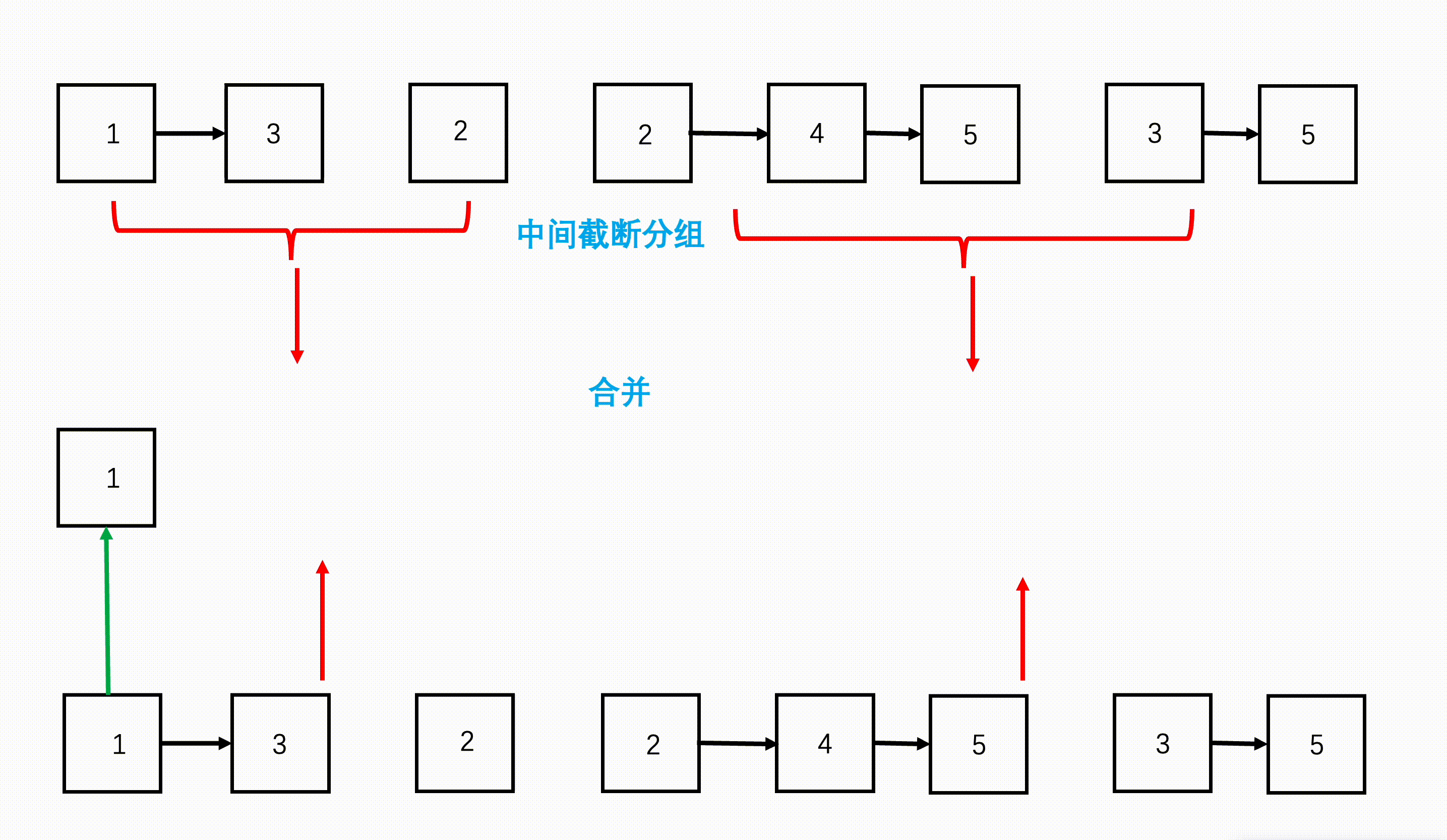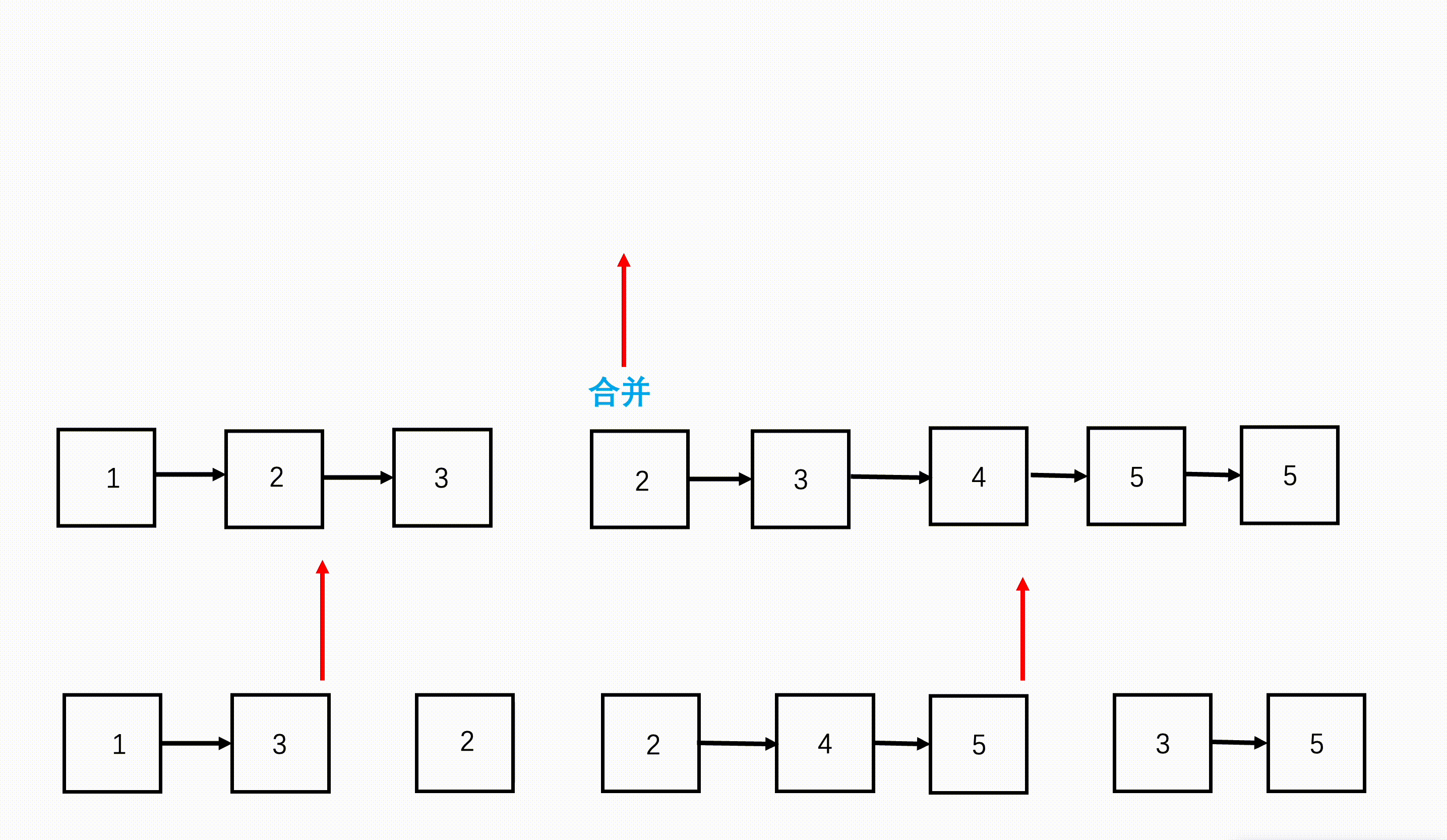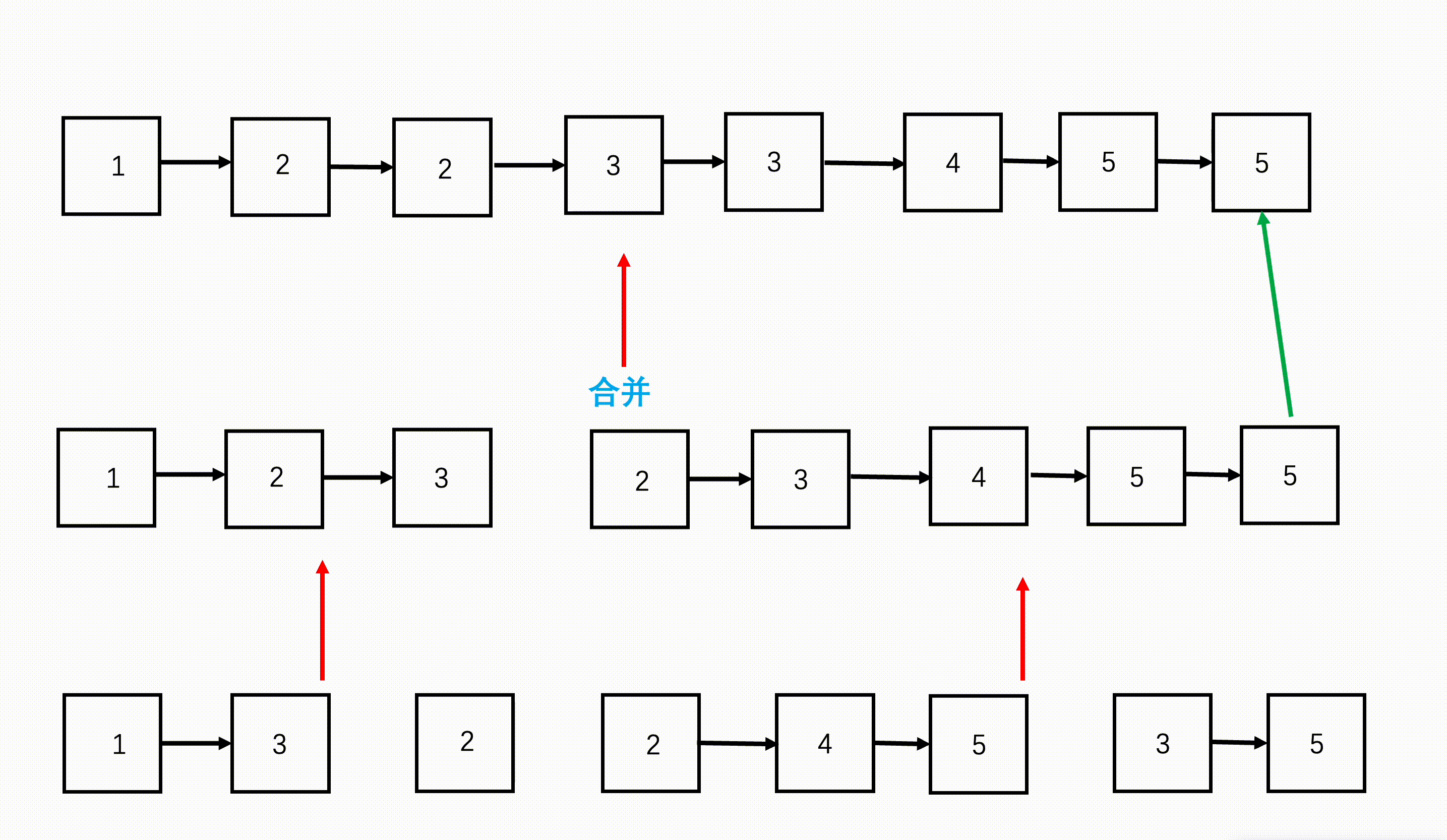
归并排序合并 k 个升序链表
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public ListNode mergeKLists(ArrayList<ListNode> lists) {
    return divideMerge(lists, 0, lists.size() - 1);
}
// 划分合并区间函数
public ListNode divideMerge(ArrayList<ListNode> lists, int left, int right) {
    if (left > right) // base case
        return null;
    else if (left == right) // 中间 1 个的情况
        return lists.get(left);
    // 从中间分成两段，再将合并好的两段合并
    int mid = left + ((right - left) >> 1);
    return merge(divideMerge(lists, left, mid), divideMerge(lists, mid + 1, right));
}
// 合并两个有序链表
public ListNode merge(ListNode list1, ListNode list2) {
    // 一个链表为空，直接返回另一个
    if (list1 == null)
        return list2;
    if (list2 == null)
        return list1;
    // 添加一个表头
    ListNode pivot = new ListNode(-1);
    ListNode cur = pivot;
    // 两个链表都不能为空
    while (list1 != null && list2 != null) {
        // 取较小值的节点
        if (list1.val <= list2.val) {
            cur.next = list1;
            // 只移动取了值的指针
            list1 = list1.next;
        } else {
            cur.next = list2;
            // 只移动取了值的指针
            list2 = list2.next;
        }
        // 指针后移
        cur = cur.next;
    }
    // 哪个链表还剩，直接连在后面
    if (list1 != null)
        cur.next = list1;
    else
        cur.next = list2;
    // 返回值去掉表头
    return pivot.next;
}

时间复杂度

\(O(nlog_2k)\)

n 为所有链表总节点数，分治为二叉树型递归，最坏情况下二叉树每层合并都是 \(O(n)\) 个节点，因为分治一共有 \(O(log_2k)\) 层。

空间复杂度

\(O(log_2k)\)

最坏情况下递归 \(log_2k\) 层，需要 \(log_2k\) 的递归栈。

F2：优先级队列

思路

不同于方法 1，该方法直接使用 k 个指针，每次比较得出 k 个数字中的最小值。

每次优先级队列中有 k 个元素，可以直接拿出最小的元素，再插入下一个元素，相当于每次都是链表的 k 个指针在比较大小，只移动最小元素的指针。

步骤
  1. 构造一个小根堆（优先级队列）；
  2. 先遍历 k 个链表头，将不是空节点的节点加入小根堆；
  3. 每次依次弹出小根堆中的最小元素，将其连接在合并后的链表后面，然后将这个节点的原链表中的后序节点（不为空的话）加入队列，与方法 1 归并排序双指针的过程类似。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public ListNode mergeKLists(ArrayList<ListNode> lists) {
    // 小根堆
    PriorityQueue<ListNode> pq = new PriorityQueue<>((l1, l2) -> l1.val - l2.val);
    // 遍历所有链表的头节点
    for (int i = 0; i < lists.size(); i++) {
        // 不为空加入小根堆
        if (lists.get(i) != null)
            pq.add(lists.get(i));
    }
    // 哨兵表头
    ListNode pivot = new ListNode(-1);
    ListNode cur = pivot;
    // 直到小根堆为空
    while (!pq.isEmpty()) {
        // 取出最小节点
        ListNode pollNode = pq.poll();
        // 连接
        cur.next = pollNode;
        cur = cur.next;
        // 如果当前最小节点的后序节点不为空，加入小根堆
        if (pollNode.next != null) {
            pq.add(pollNode.next);
        }
    }
    // 去掉哨兵节点
    return pivot.next;
}
时间复杂度

\(O(nlog_2k)\)

n 为所有链表总节点数，最坏要遍历所有节点，每次加入优先级队列排序需要 \(O(log_2k)\)

空间复杂度

\(O(k)\)

优先队列的大小不会超过 k

BM6 判断链表中是否有环

描述

判断给定的链表中是否有环。如果有环则返回 true，否则返回 false。

F1：双指针

思路

线性与环形链表特点：

  • 线性链表末尾一定有 null。

  • 环形链表的环一定在末尾，末尾没有 null 了。

线性与环形链表结束条件：

  • 线性链表的结束条件就是遍历到 null。

  • 环形链表会不断循环，需要借助双指针才能结束。同向访问的双指针，因为速度不同，只要有环，二者一定能相遇。

步骤
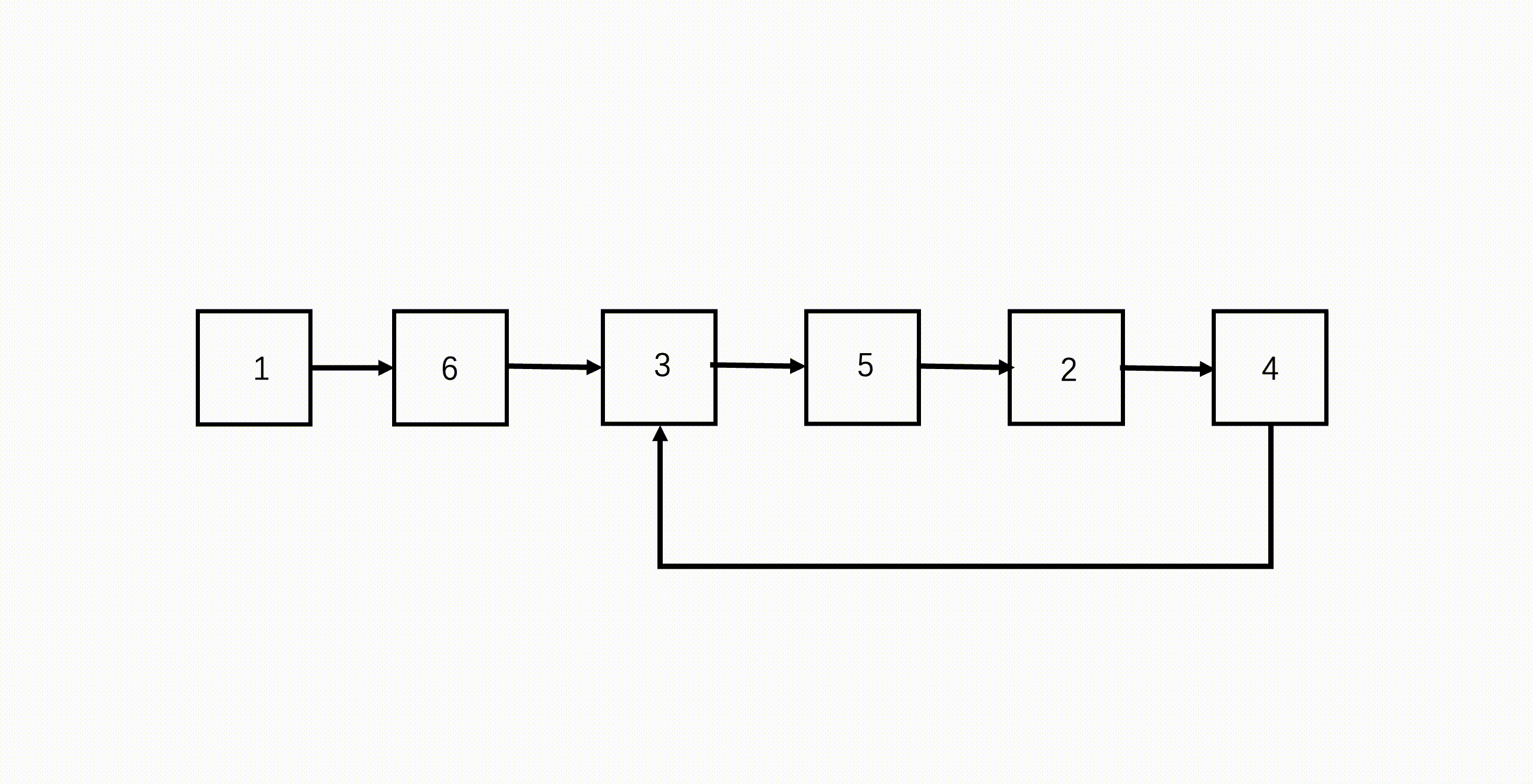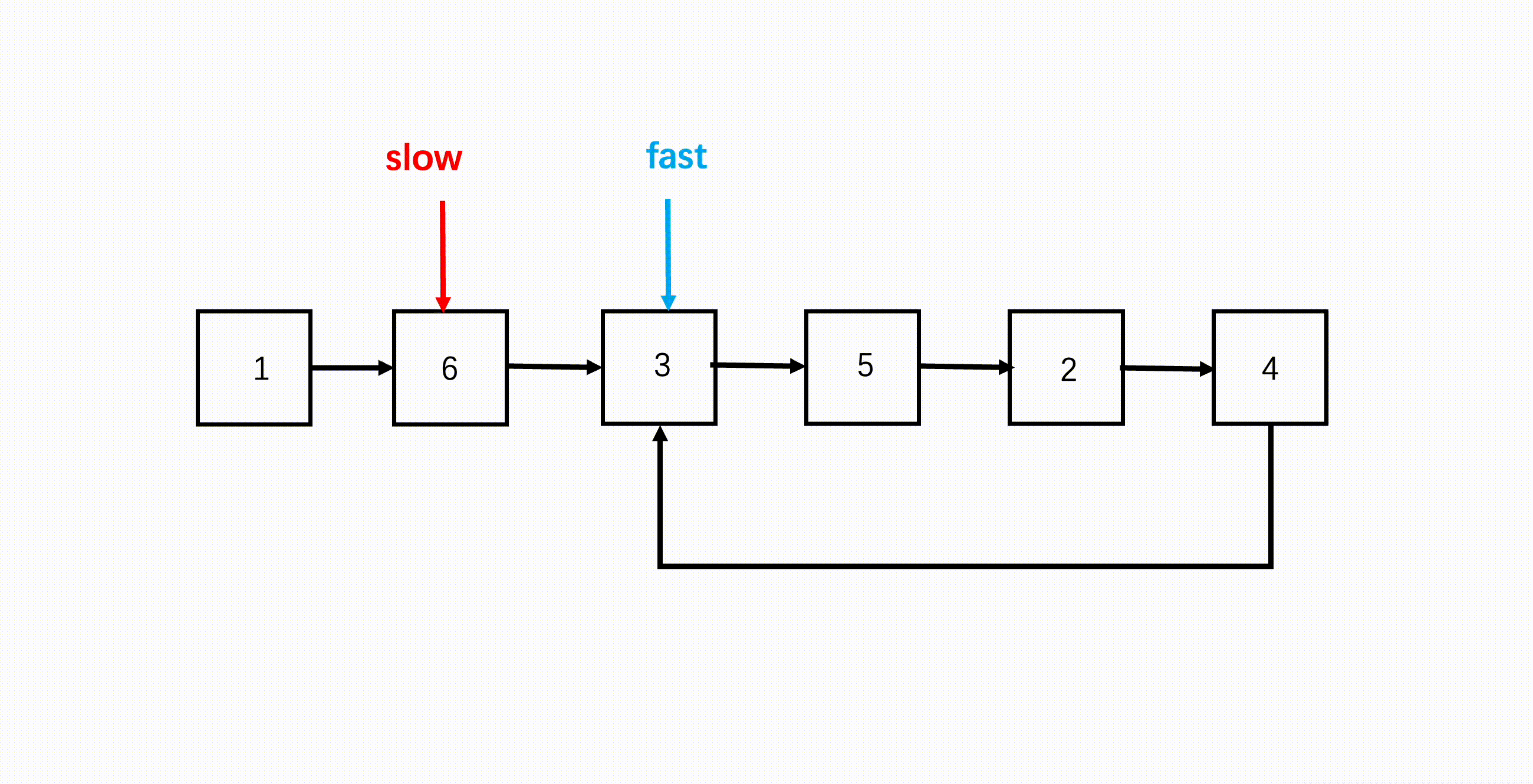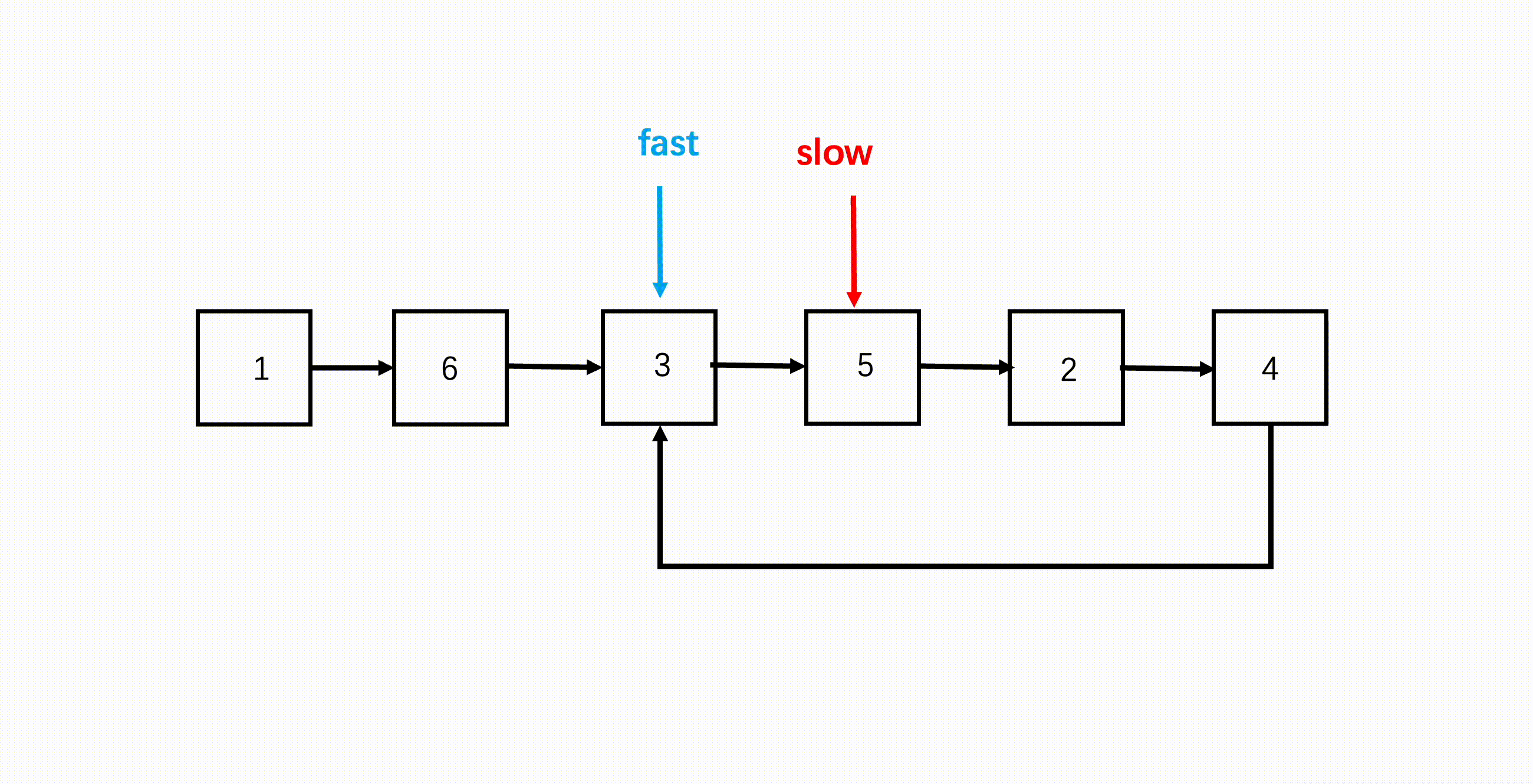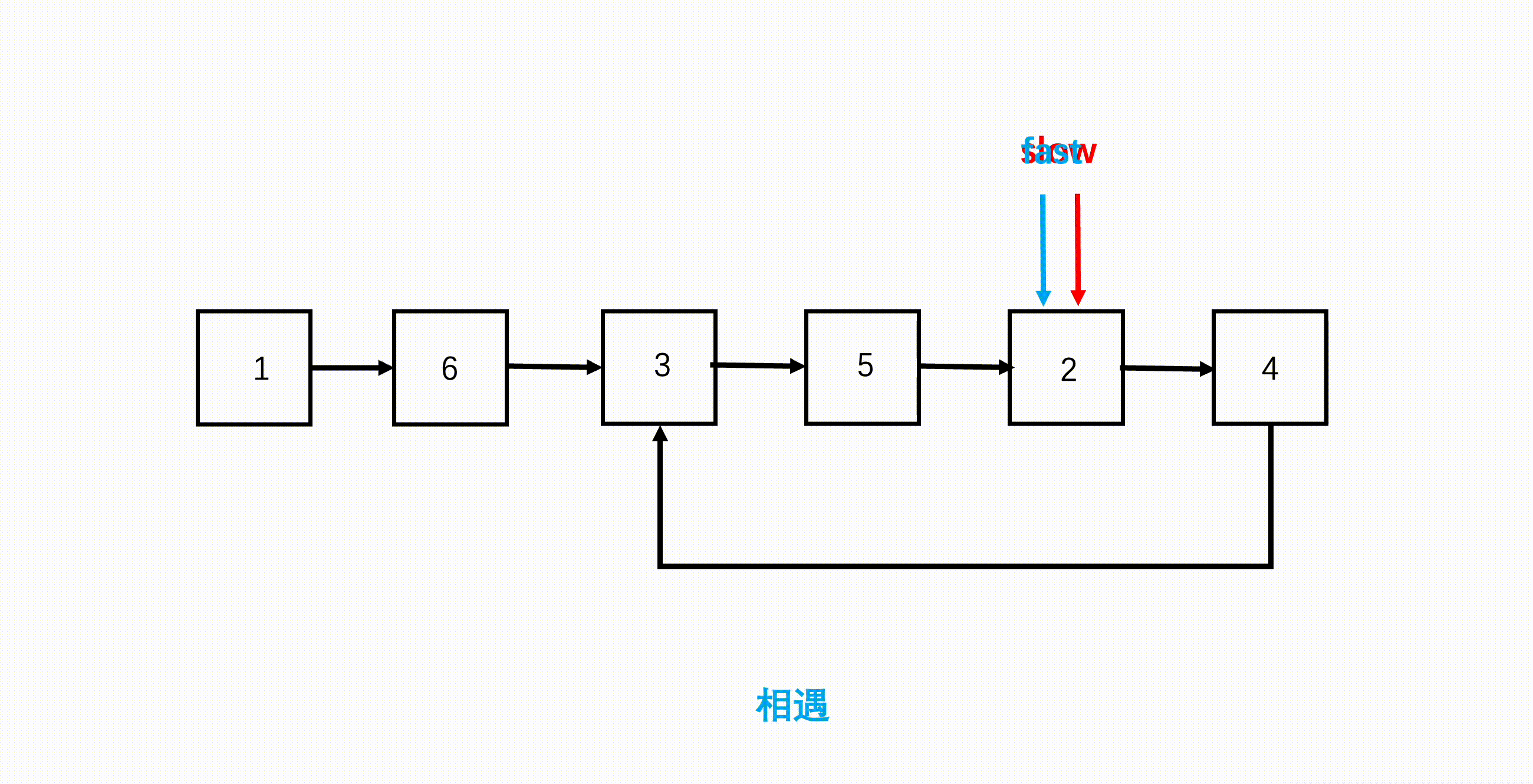
  1. 设置快慢两指针，初始都指向链表头；
  2. 遍历链表，快指针每次走两步，慢指针每次走一步；
  3. 如果快指针到了链表末尾，说明没有环，因为它每次走两步，所以要验证连续两步是否为 null；
  4. 如果链表有环，那快慢双指针会在环内循环，因为快指针每次走两步，因此快指针会在环内追到慢指针，二者相遇就代表有环。
双指针判断链表是否有环
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public boolean hasCycle(ListNode head) {
    // 先判断链表为空的情况
    if (head == null)
        return false;
    // 1. 设置快慢两指针，初始都指向链表头
    ListNode fast = head;
    ListNode slow = head;
    // 2. 遍历链表
    // 3. 如果没环，fast 会先到链表尾
    while (fast != null && fast.next != null) {
        // 快指针移动两步
        fast = fast.next.next;
        // 慢指针移动一步
        slow = slow.next;
        // 相遇则有环
        if (fast == slow)
            return true;
    }
    // 到末尾，则没有环
    return false;
}
时间复杂度

\(O(M)\)

最坏情况下遍历链表 n 个节点。

空间复杂度

\(O(1)\)

仅使用了两个指针，没有额外辅助空间。

BM7 链表中环的入口点

描述

给一个长度为 n 链表，若其中包含环，请找出该链表的环的入口结点，否则，返回 null。

分解任务
  1. 判断链表是否有环；
  2. 在有环的链表中找到环的入口。

F1：双指针

思路

如何找到环的入口？

一个有环链表。

假设快指针在环中走了 \(n\) 圈，慢指针走了 \(m\) 圈，两者相遇。

链表头节点到环入口点距离为 \(x\)，环入口到相遇点距离为 \(y\)，相遇点到环入口点距离为 \(z\)。

快指针一共走了 \(x + n(y + z) + y\) 步，慢指针一共走了 \(x + m(y + z) + y\) 步。

快指针走的步数是慢指针的两倍，则 \[ x + n(y + z) + y = 2(x + m(y + z) + y) \] 进一步推导， \[ x+y=(n-2m)(y+z) \] 因为环的大小是 \(y+z\)，说明从链表头经过环入口到达相遇地方经过的距离等于整数倍环的大小。那么，我们从头开始遍历到相遇位置，和从相遇位置开始在环中遍历，会使用相同的步数，而双方最后都会经过入口到相遇位置这 \(y\) 个节点，说明这 \(y\) 个节点它们就是重叠遍历的，那它们从入口位置就相遇了，这样就找到了入口节点。

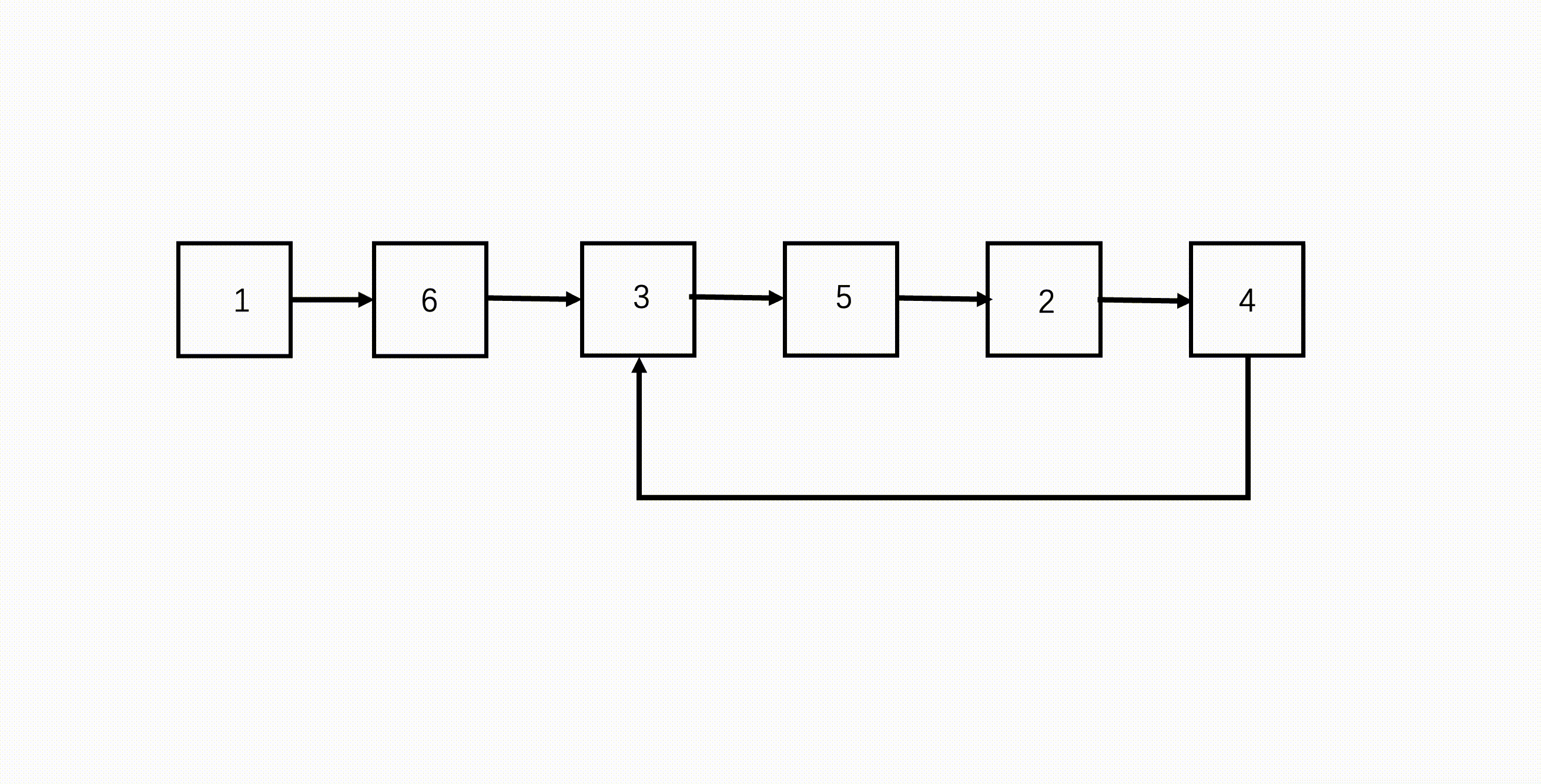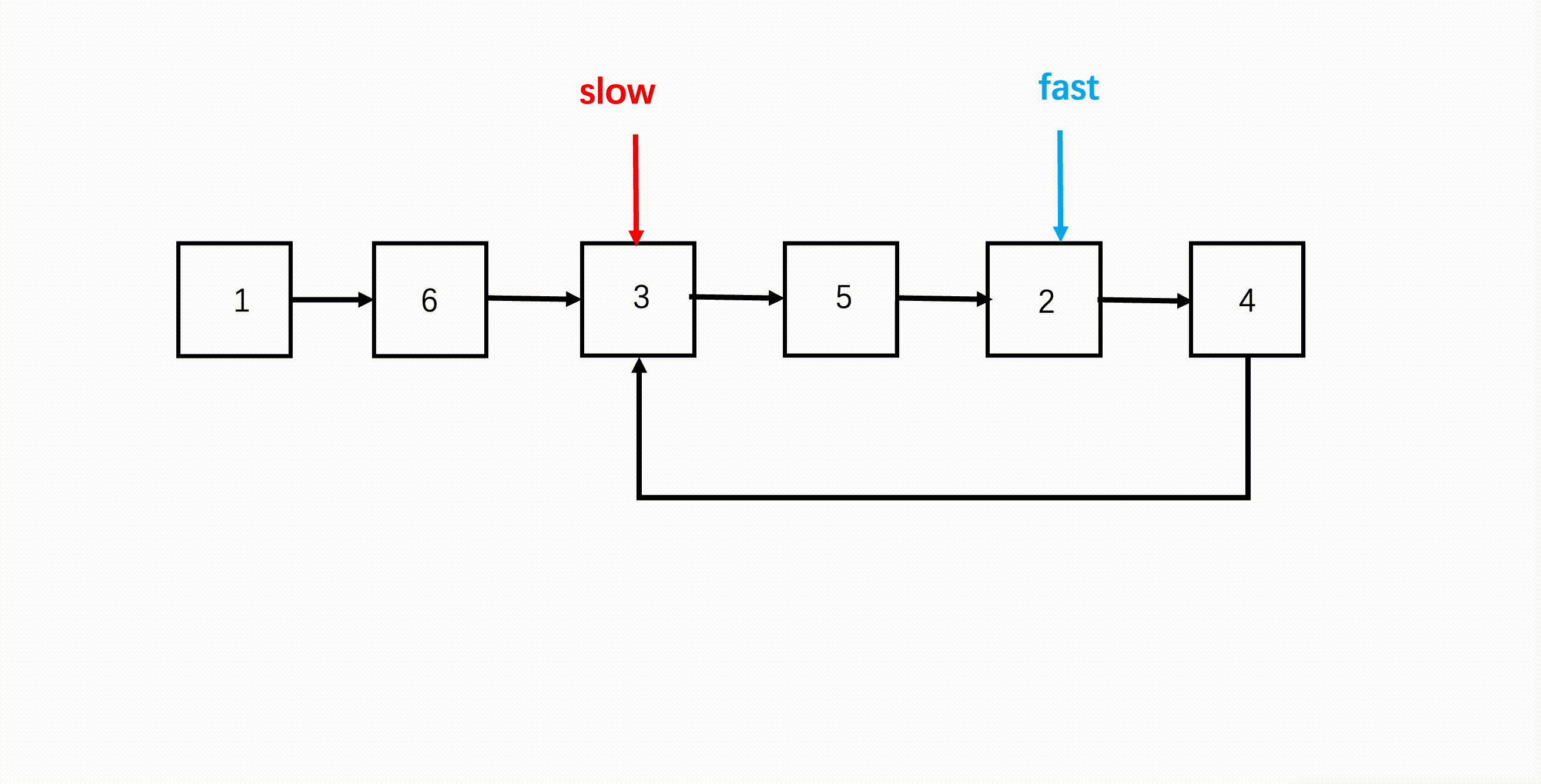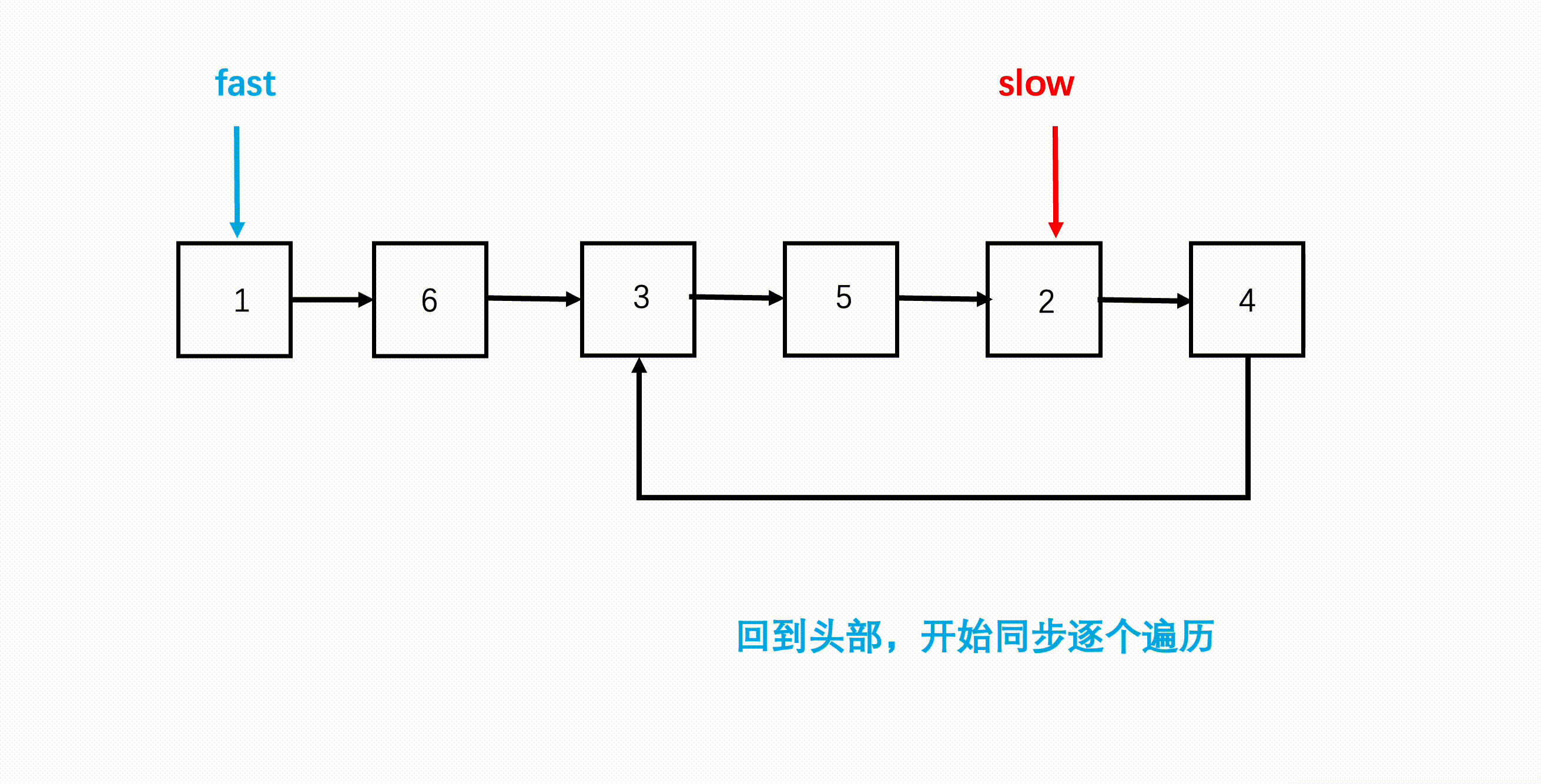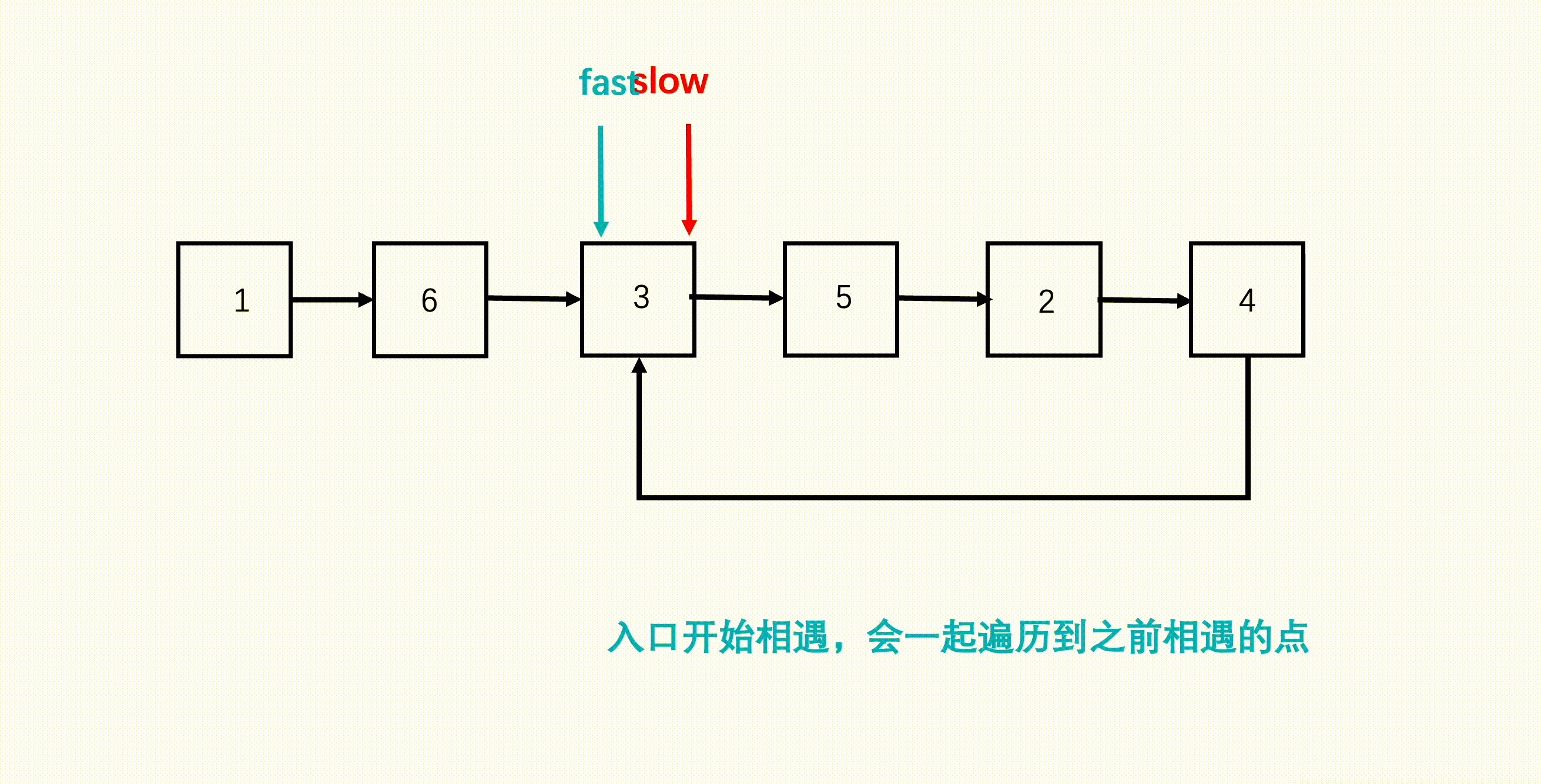
步骤
  1. 使用 BM6 方法判断链表是否有环，并找到相遇节点。
  2. 慢指针继续在相遇节点，快指针回到链表头，两个指针同步逐个元素开始遍历链表。
  3. 两者再次相遇的地方就是环的入口。
双指针找环入口
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// 寻找链表中环的入口节点
public ListNode entryNodeOfLoop(ListNode pHead) {
    ListNode slow = hasCycle(pHead);
    // 没有环
    if (slow == null)
        return null;
    // 有环
    // 快指针回到表头
    ListNode fast = pHead;
    // 再次相遇即是环入口
    while (fast != slow) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}

// 判断有没有环
public ListNode hasCycle(ListNode head) {
    // 先判断链表为空的情况
    if (head == null)
        return null;
    // 快慢双指针
    ListNode fast = head;
    ListNode slow = head;
    // 如果没环，快指针会先到链表尾
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        // 相遇则有环，返回相遇的节点
        if (slow == fast) {
            return slow;
        }
    }
    // 到末尾说明没有换，返回 null
    return null;
}
时间复杂度

\(O(n)\)

最坏情况下遍历链表两次

空间复杂度

\(O(1)\)

使用了常数个指针，没有额外辅助空间

BM8 链表中倒数最后 k 个节点

描述

输入一个长度为 n 的链表，设链表中的元素的值为 ai ，返回该链表中倒数第 k 个节点。

如果该链表长度小于 k，请返回一个长度为 0 的链表。

F1：双指针（推荐）

思路

链表无法逆序遍历。

如果当前我们处于倒数第 k 的位置上，即距离链表尾的距离是 k。

我们假设双指针指向这两个位置，二者同步向前移动，当前面快指针到了链表尾的时候，两个指针之间的距离还是 k。

虽然无法让指针逆向移动，但是上述思路却可以正向实施。

步骤
  1. 准备一个快指针，从链表头开始，在链表上先走 k 步。
  2. 准备慢指针指向原始链表头，代表当前节点，快慢指针之间的距离一直都是 k。
  3. 快慢指针同步移动，当快指针到达链表尾部的时候，慢指针正好到了倒数 k 个节点的位置。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public ListNode FindKthToTail(ListNode pHead, int k) {
    ListNode fast = pHead;
    ListNode slow = pHead;
    // 快指针先行 k 步
    for (int i = 0; i < k; i++) {
        if (fast != null) {
            fast = fast.next;
        } else { // 达不到 k 步，说明链表过短。
            return slow = null;
        }
    }
    // 快慢指针同步，快指针先到底，慢指针指向倒数第 k 个
    while (fast != null) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}
时间复杂度

\(O(n)\)

总共遍历 n 个链表节点

空间复杂度

\(O(1)\)

常数级指针变量，无额外辅助空间使用

F2：先找长度再找最后 k

思路

链表不能逆向遍历，也不能直接访问。但是对于倒数第 k 个位置，我们只需知道是正数多少位，还是可以直接遍历得到的。

步骤
  1. 遍历链表，找到链表的长度；
  2. 如果链表长度小于 k，返回空节点。
  3. 如果链表长度够长，我们从头节点往后遍历 n - k 次即可。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public ListNode FindKthToTail(ListNode pHead, int k) {
    int n = 0;
    ListNode cur = pHead;
    // 遍历链表，统计链表长度
    while (cur != null) {
        n ++;
        cur = cur.next;
    }
    // 链表长度不足 k，返回 null
    if (n < k) {
        return null;
    }
    cur = pHead;
    // 遍历 n - k 次
    for (int i = 0; i < n - k; i++) {
        cur = cur.next;
    }
    return cur;
}
时间复杂度

\(O(n)\)

最坏情况下，两次遍历 n 个链表元素

空间复杂度

\(O(1)\)

常数级指针变量，无额外辅助空间使用

BM9 删除链表的倒数第 n 个节点

描述

给定一个链表，删除链表的倒数第 n 个节点并返回链表的头指针

例如，给出的链表为: 1 -> 2 -> 3 -> 4 -> 5, n = 2。删除了链表的倒数第 n 个节点，链表变为 1 -> 2 -> 3 -> 5。

备注：题目保证 n 一定是有效的。

F1：三指针

思路

思路与 BM8 链表中倒数最后 k 个节点的思路基本一致，不同的是，在其基础上增加一个哨兵表头以及一个指针。

步骤
  1. 给链表添加一个表头，处理删掉第一个元素时比较方便。
  2. 准备一个快指针，在链表上先走 n 步。
  3. 准备一个慢指针指向原始链表头，一个前序指针指向添加的表头。快慢指针之间的距离一直都是 n，前序指针始终指向慢指针的前序节点。
  4. 三指针同步向前移动，当快指针到达链表尾部 null 的时候，慢指针正好到了倒数第 n 个节点。
  5. 将前序指针指向的前序节点的指针指向慢指针后一个节点，删除掉慢指针指向的节点。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public ListNode removeNthFromEnd(ListNode head, int n) {
    // 添加表头
    ListNode pivot = new ListNode(-1);
    pivot.next = head;
    // 前序指针
    ListNode pre = pivot;
    // 慢指针
    ListNode slow = head;
    // 快指针
    ListNode fast = head;
    // 快指针先走 n 步
    while (n != 0) { // 题目保证了 n 一定有效
        fast = fast.next;
        n--;
    }
    // 三指针同步前移，快指针到达末尾，慢指针就到了倒数第 n 个位置
    while (fast != null) {
        fast = fast.next;
        pre = pre.next;
        slow = slow.next;
    }
    // 删除慢指针节点
    pre.next = slow.next;
    // 去掉表头返回
    return pivot.next;
}
时间复杂度

\(O(n)\)

最坏情况下，遍历 n 个链表节点。

空间复杂度

\(O(1)\)

常数级指针变量，无额外辅助空间使用

BM10 两个链表的第一个公共节点

描述

输入两个无环的单向链表，找出它们的第一个公共结点，如果没有公共节点则返回空。

F1：双指针

思路

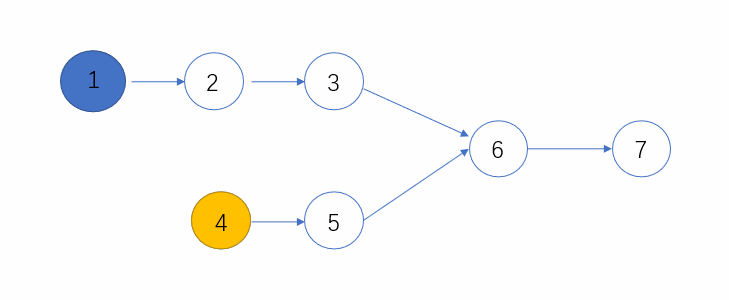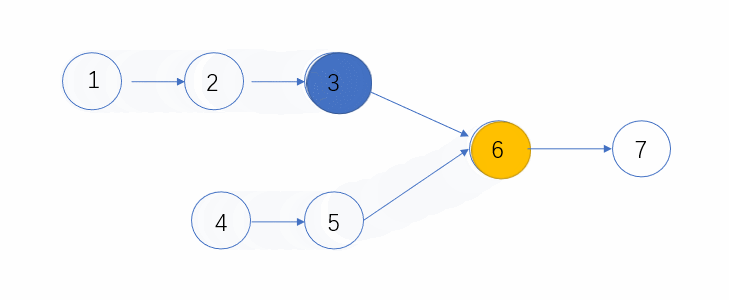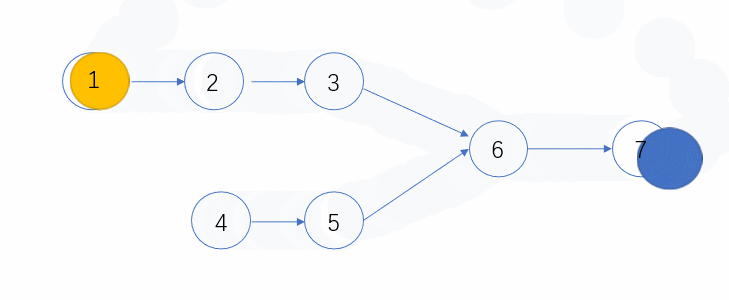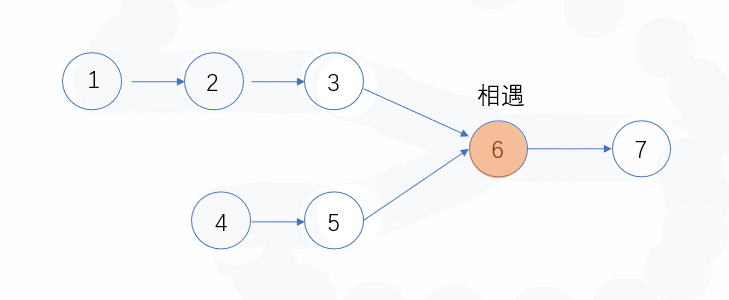
使用两个指针 p1，p2，一个从链表 1 的头节点开始遍历，一个从链表 2 的头节点开始遍历。

p1、p2 一起遍历，若 p1 先走到链表 1 的尽头（null），则从链表 2 的头节点继续遍历。同样的，如果 p2 先走到链表 2 的尽头（null），则从链表 1 的头节点继续遍历，也就是说，p1 和 p2 都会遍历链表 1 和链表 2.

两个指针，同样的速度，走完同样的长度（链表 1 + 链表 2），不管两条链表有无相同节点，都能够同时到达终点。

因此，如何确定公共节点：

  • 有公共节点的时候，p1 和 p2 必会相遇，因为长度一样，速度也一样，必会走到相同的地方。两者相遇的节点就是第一个公共的节点。
  • 无公共节点的时候，此时 p1 和 p2 都会走到终点，那么他们此时都是 null，也算相等。
双指针确定两链表第一个公共节点
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
    // 1. 定义两个指针
    ListNode p1 = pHead1, p2 = pHead2;
    // 2. 指针遍历两个链表
    while (p1 != p2) {
        // p1 到链表 1 终点就从链表 2 开始遍历，否则继续向后遍历
        p1 = (p1 == null) ? pHead2 : p1.next;
        // p2 到链表 2 终点就从链表 1 开始遍历，否则继续向后遍历
        p2 = (p2 == null) ? pHead1 : p2.next;
    }
    // 3. 相遇节点就是两个链表的第一个公共节点
    return p1;
}
时间复杂度

\(O(m+n)\)

链表 1 和链表 2 的长度之和。

空间复杂度

\(O(1)\)

常数级指针变量，无额外辅助空间使用。

BM13 判断一个链表是否为回文结构

描述

给定一个链表，请判断该链表是否为回文结构。

回文是指该字符串正序逆序完全一致。

F1：栈逆序

步骤
  1. 遍历链表，将链表元素依次加入栈中。
  2. 依次从栈中弹出元素，和链表的顺序遍历比较，如果都是相同的，那么就是回文，否则就不是。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public boolean isPail (ListNode head) {
    // write code here
    if (head == null || head.next == null)
        return true;
    Stack<Integer> stack = new Stack<>();
    ListNode cur = head;
    // 遍历节点，放入栈中
    while(cur != null) {
        stack.push(cur.val);
        cur = cur.next;
    }
    cur = head;
    // 正向遍历与反向遍历对比
    while(!stack.isEmpty()) {
        int popVal = stack.pop();
        // 如果值不等，不是回文结构
        if(popVal != cur.val) {
            return false;
        } else {
            cur = cur.next;
        }
    }
    // 全部相等，是回文结构
    return true;
}
时间复杂度

\(O(n)\)

n 为链表长度，遍历链表入栈为 \(O(n)\)，后续再次遍历链表和栈。

空间复杂度

\(O(n)\)

记录链表元素的辅助栈长度和链表相同。

F2: 双指针寻中逆序

步骤
  1. 慢指针每次走一个节点，快指针每次走两个节点，快指针到达链表终点（null）时，慢指针刚好到了链表中点。
  2. 从中点位置开始，将后半段链表反转。
  3. 双指针左指针指向头节点，右指针指向反转后的头节点（原链表的尾节点），都向中间遍历，依次比较对应位置的节点值是否相等。

快慢指针寻找中点：

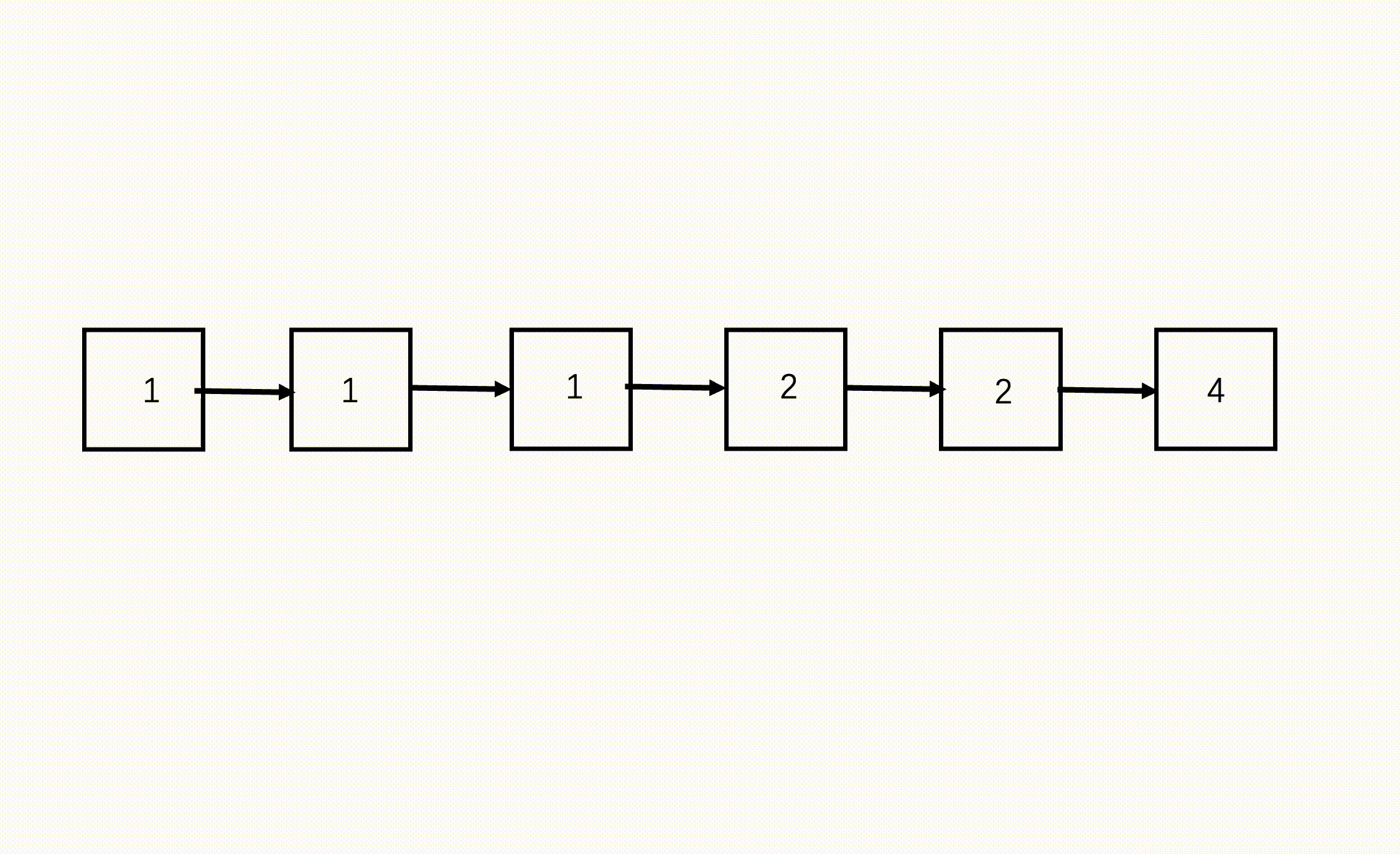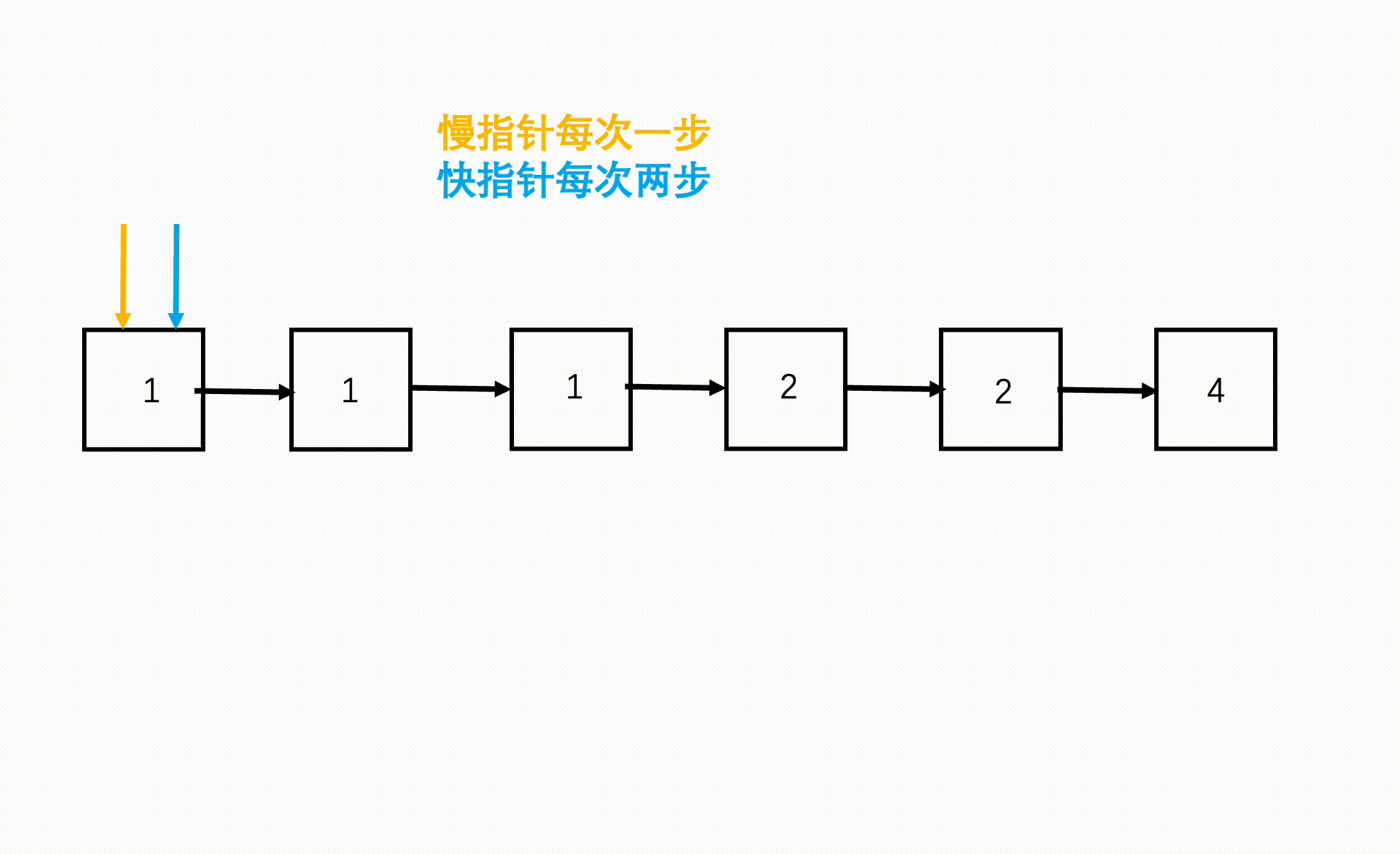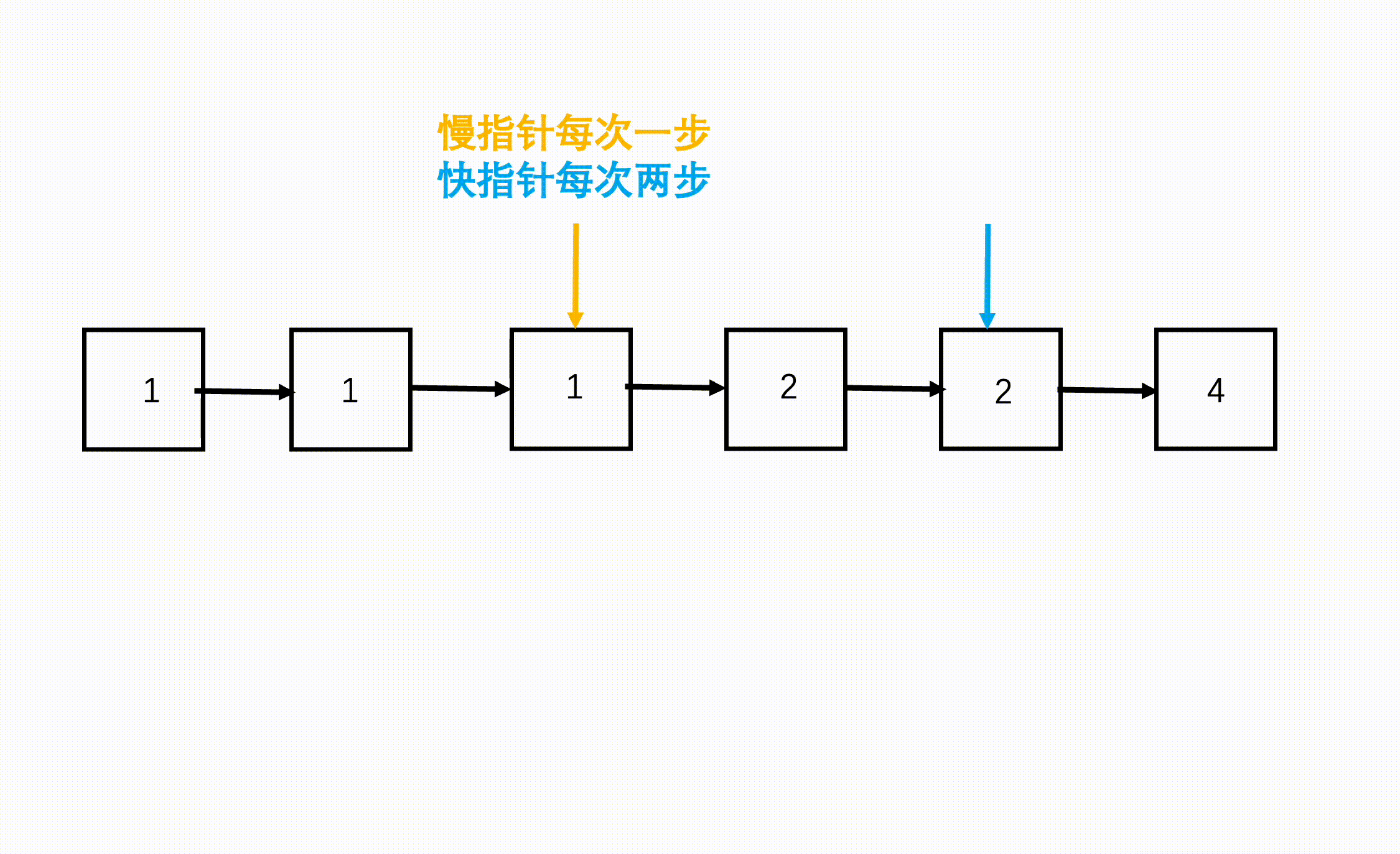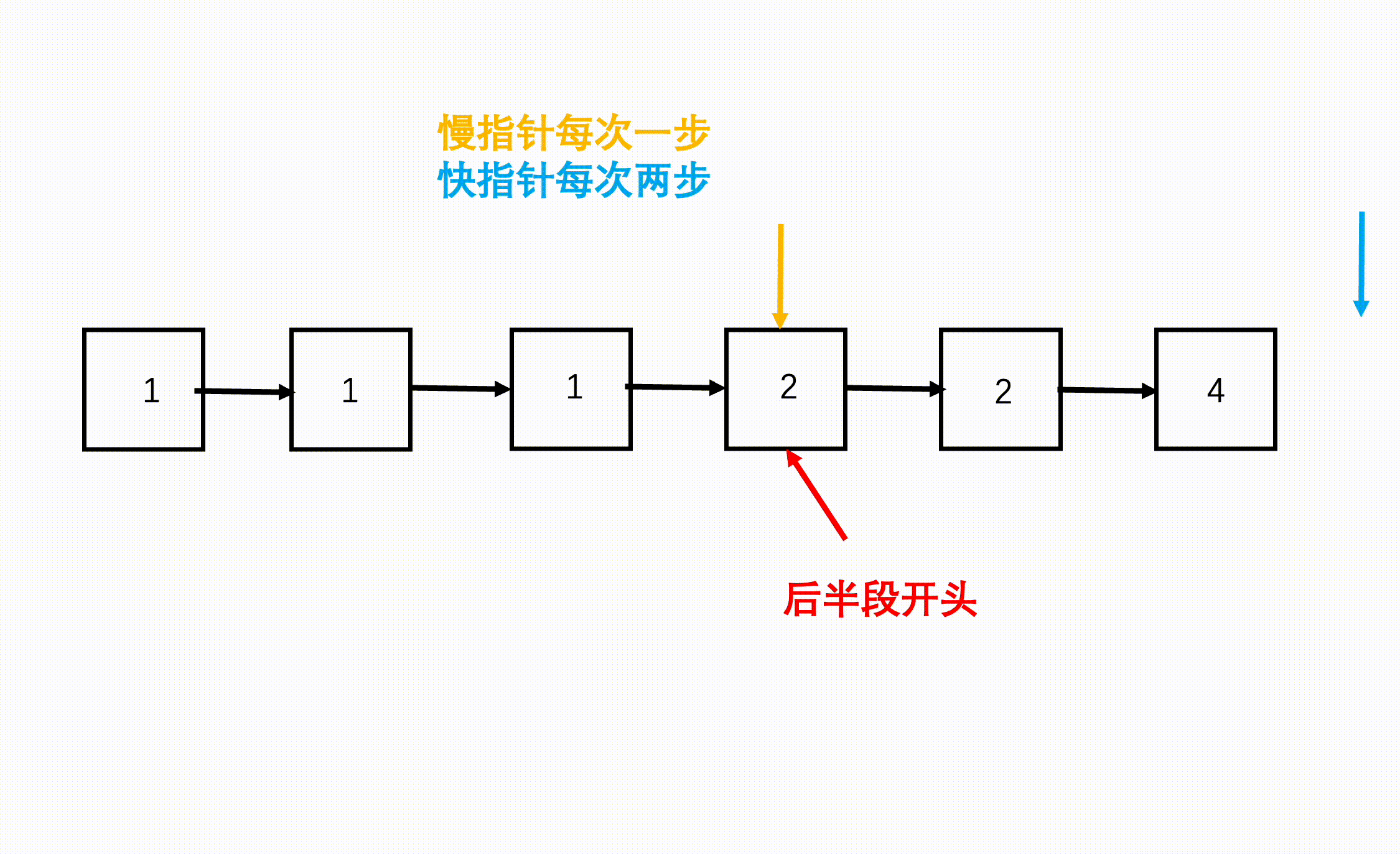
双指针寻找中点

链表反转及比较：

链表反转及比较
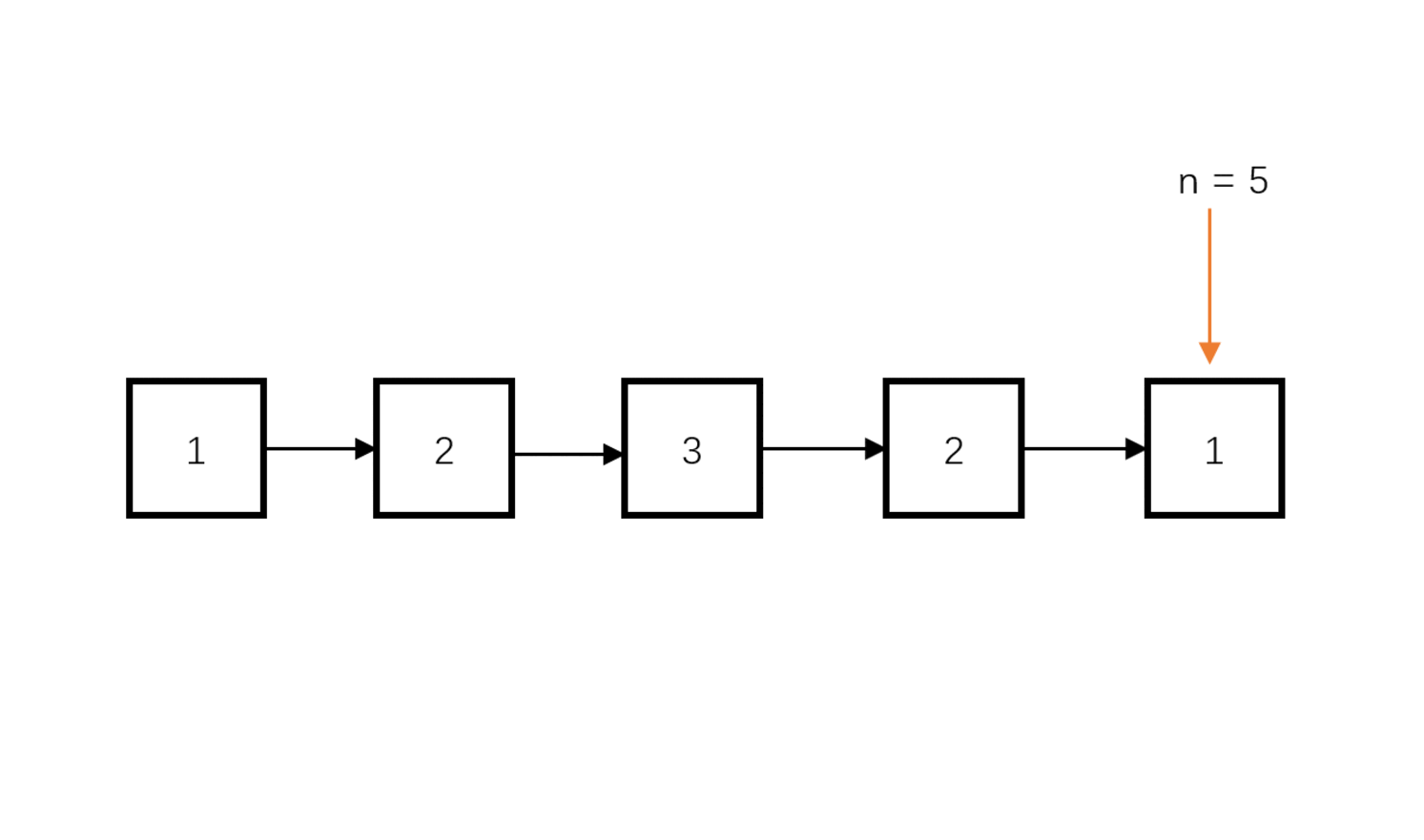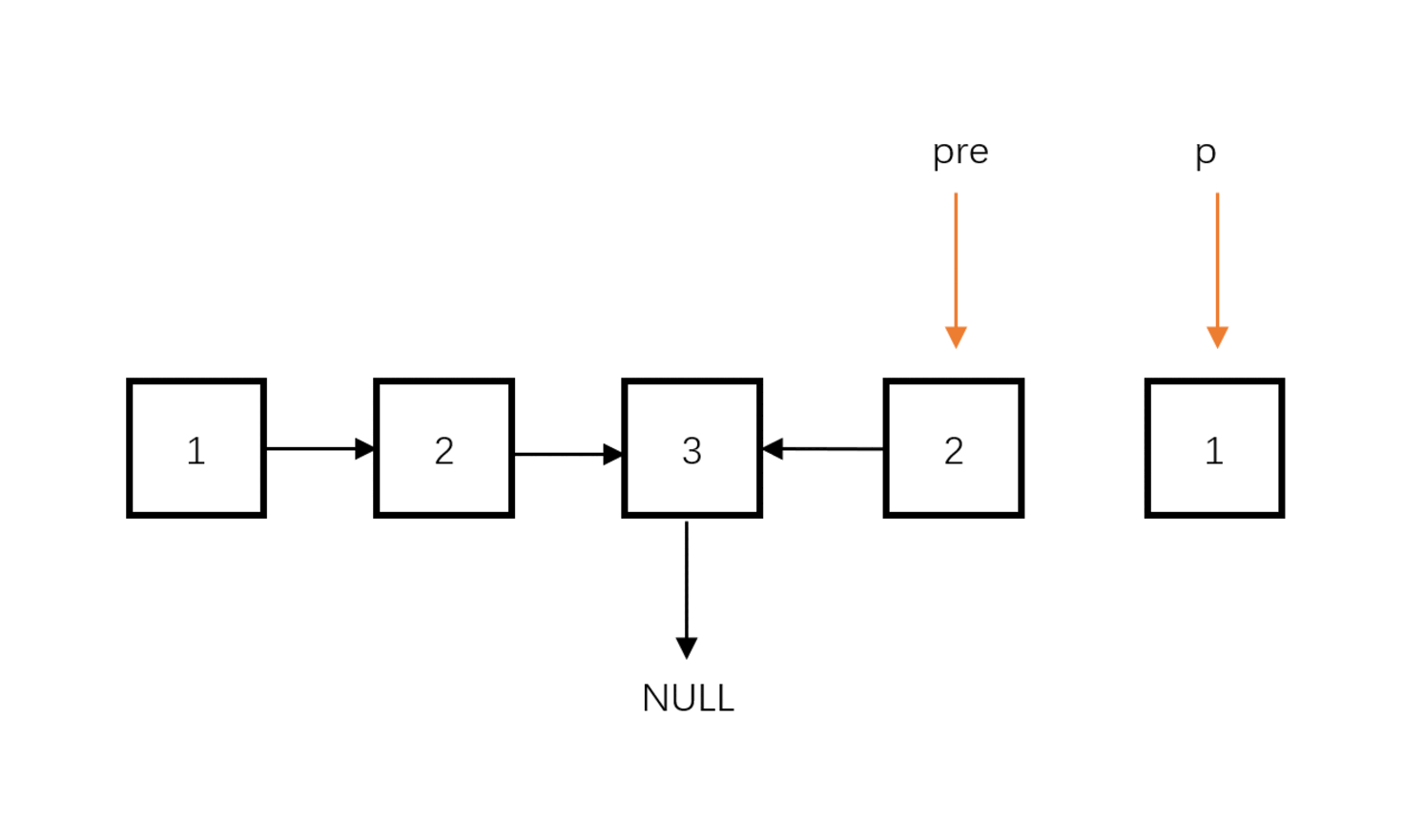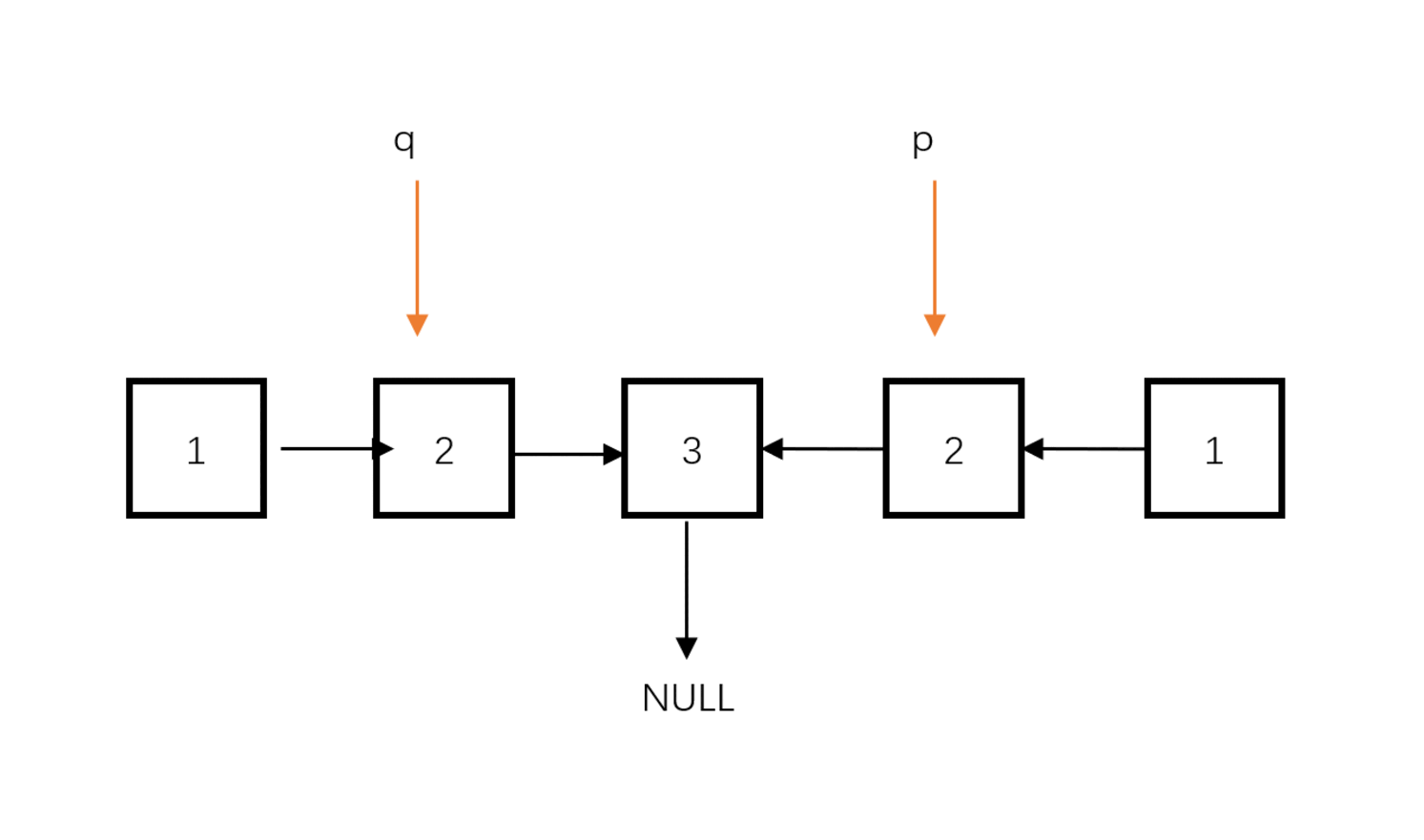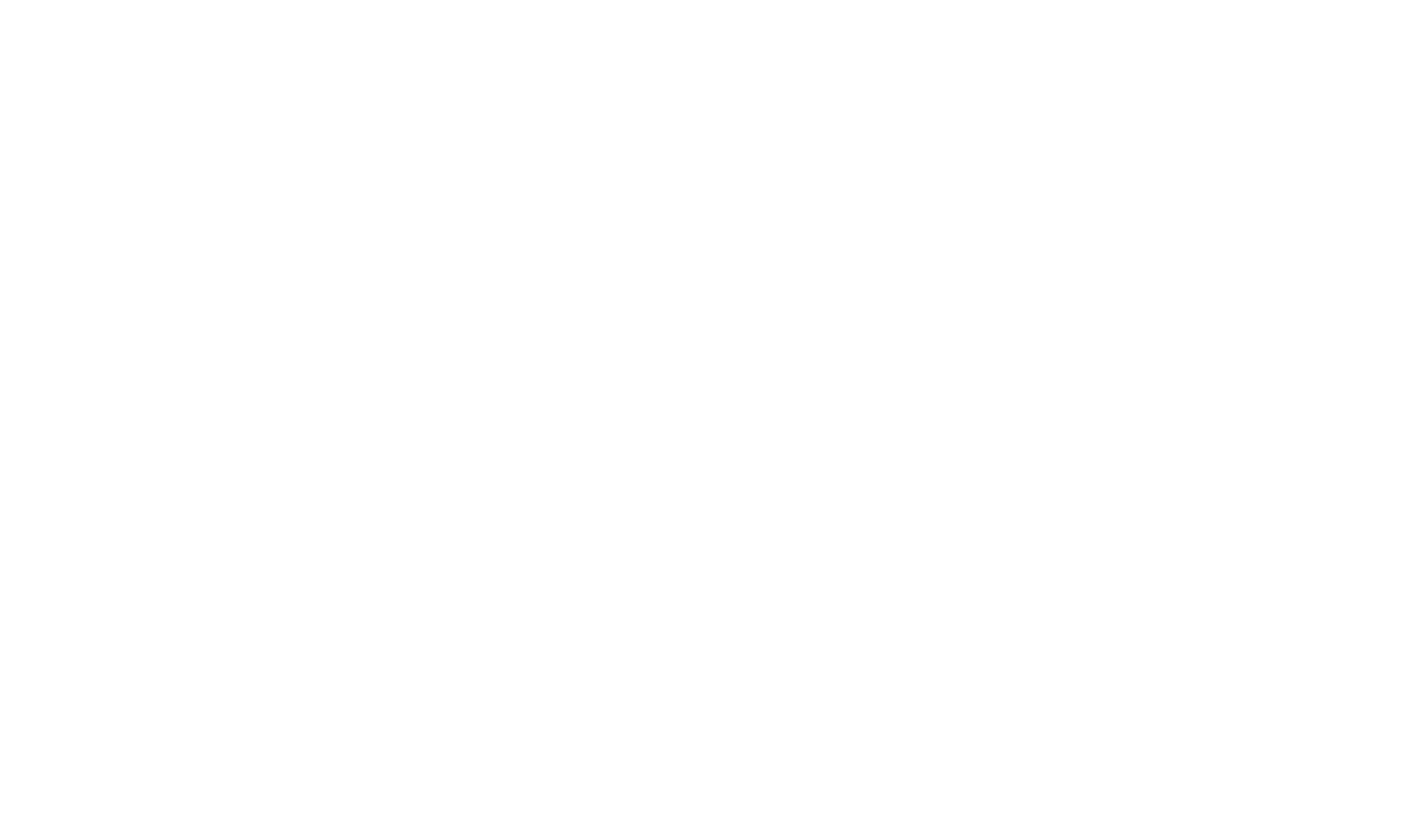
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public boolean isPail(ListNode head) {
    // 空链表为回文结构
    if (head == null)
        return true;
    // 准备快慢双指针
    ListNode slow = head;
    ListNode fast = head;
    // 双指针寻找中点
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
    }
    // 中点处开始反转
    slow = reverse(slow);
    fast = head;
    while (slow != null) {
        // 比较快慢指针所指的值是否相等
        if (slow.val != fast.val) {
            return false;
        }
        slow = slow.next;
        fast = fast.next;
    }
    return true;
}
// 反转链表
public ListNode reverse(ListNode head) {
    ListNode pre = null;
    ListNode next = null;
    ListNode cur = head;
    while (cur != null) {
        next = cur.next;
        cur.next = pre;
        pre = cur;
        cur = next;
    }
    return pre;
}
时间复杂度

\(O(n)\)

n 为链表长度，双指针找到中点遍历半个链表，后续反转链表为 \(O(n)\)，然后再遍历两份半个链表。

空间复杂度

\(O(1)\)

常数级指针变量，没有额外辅助空间。

BM14 链表的奇偶重排

描述

给定一个单链表，请设定一个函数，将链表的奇数位节点和偶数位节点分别放在一起，重排后输出。

注意是节点的编号而非节点的数值。

F1：双指针

思路

第一个节点是奇数位，第二个节点是偶数位，第三个节点又是奇数位，因此，可以断掉节点 1 和节点 2 之间的连接，节点 1 的 next 指向节点 2 后面的节点 3。断掉节点 2 与节点 3 之间的连接，指向节点 4 节点，如此直到链表结束。

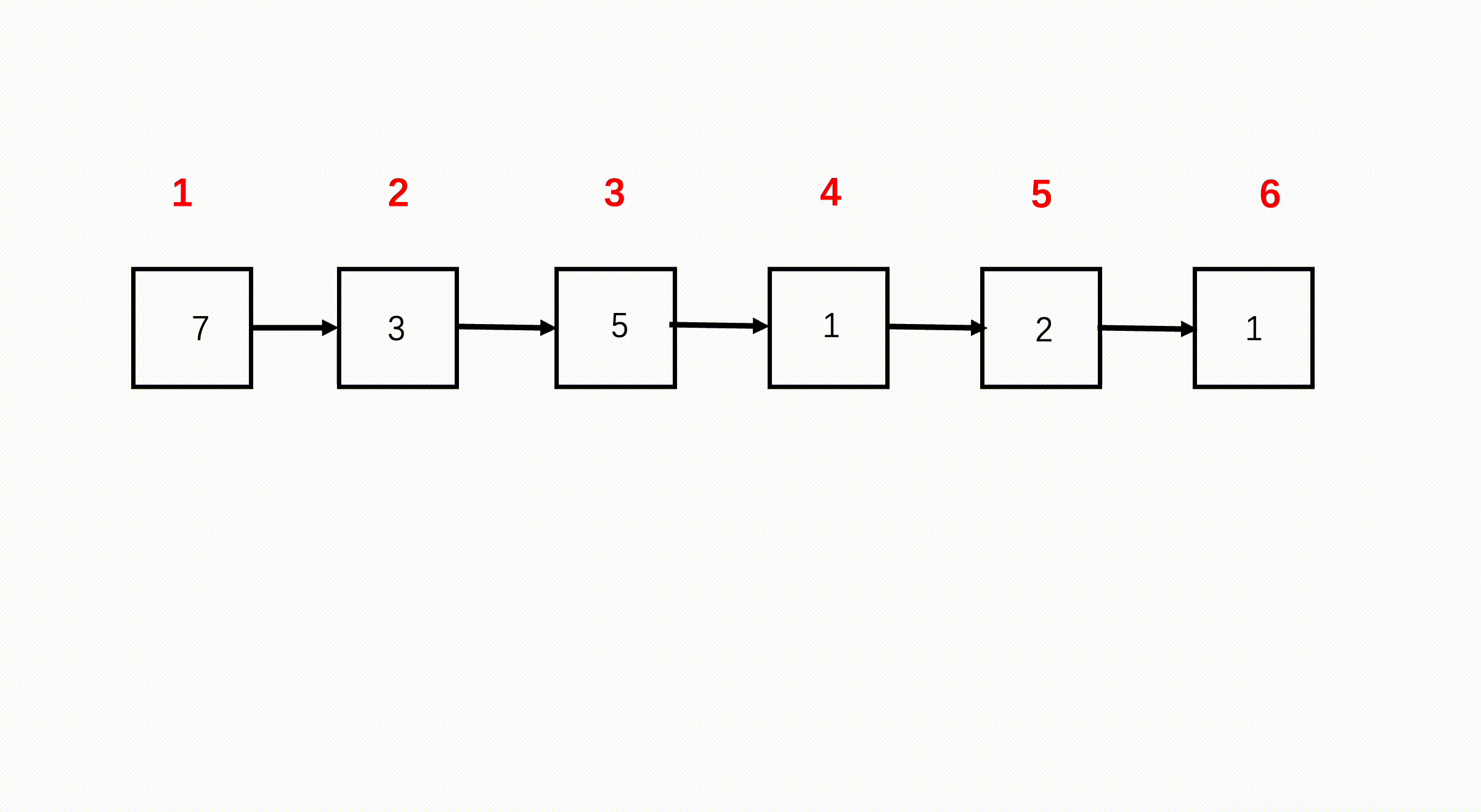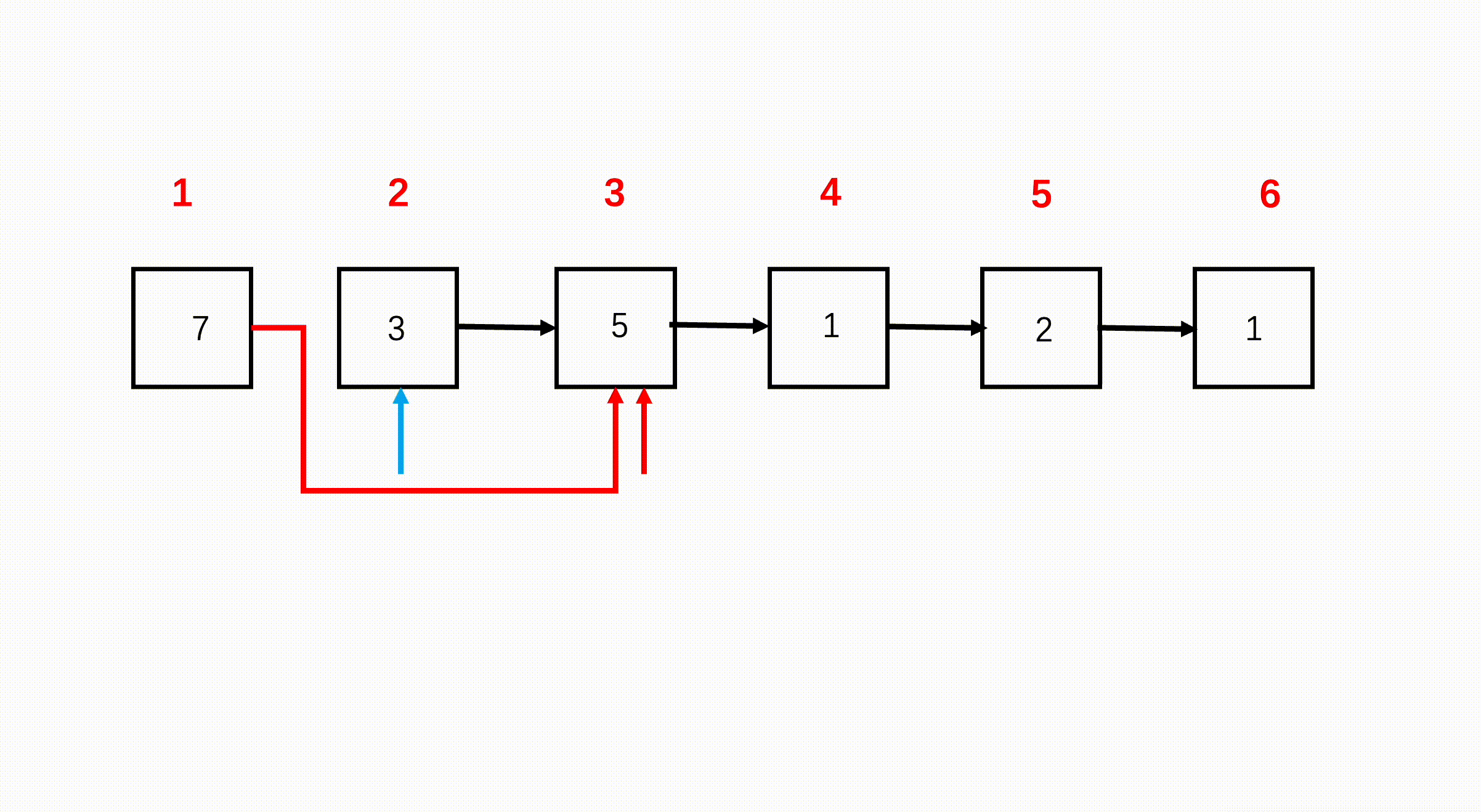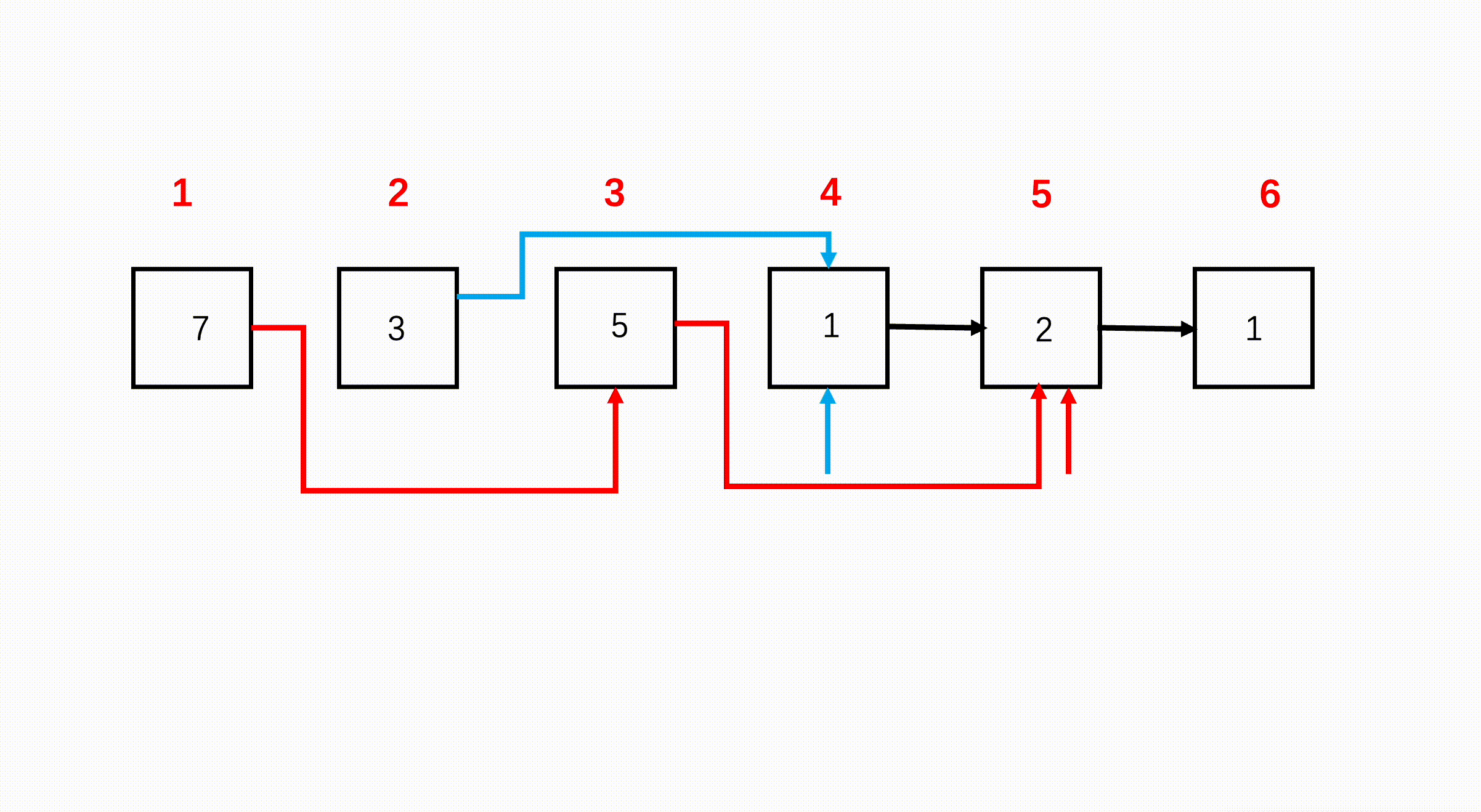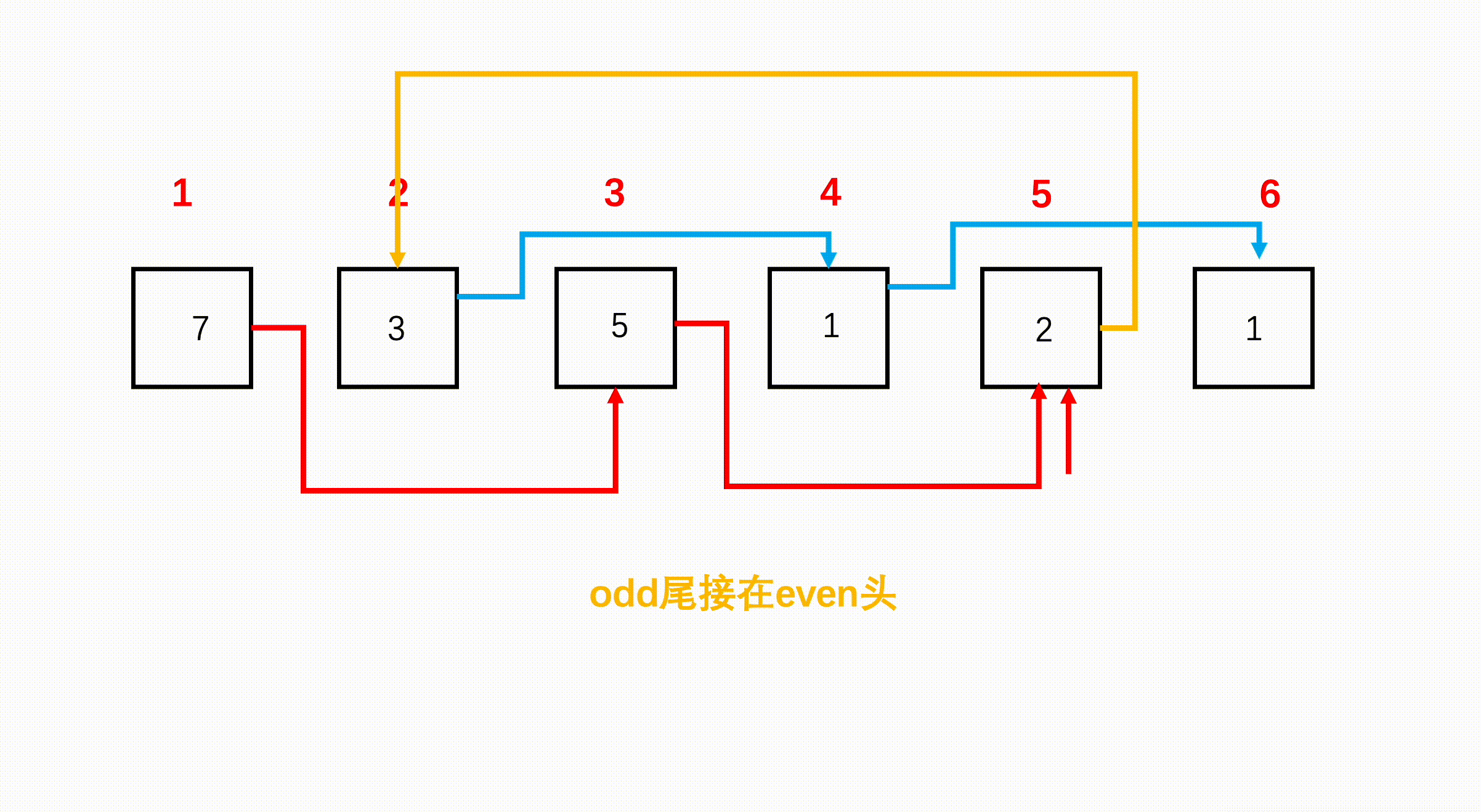
双指针奇偶位重排
步骤

  1. 判断空链表的情况，如果链表为空，不用重排。

  2. 使用双指针 odd 和 even 分别遍历奇数节点和偶数节点，并给偶数节点链表一个头。

  3. 上述过程，每次遍历两个节点，且 even 在后面，因此每轮循环用 even 检查后两个元素是否为 null，如果不是，再进入循环进行上述连接过程。

  4. 将偶数节点头接在奇数位最后一个节点后面，再返回头部。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public ListNode oddEvenList(ListNode head) {
    // 1. 如果链表为空，不用重排
    if (head == null)
        return head;
    // 2.1 奇数位节点指针指向表头
    ListNode odd = head;
    // 2.2 偶数位节点指针指向第二个节点，可能为空
    ListNode even = head.next;
    // 2.2 偶数位头节点的哨兵节点，保留住偶数位头节点
    ListNode evenPivot = even;
    // 3. 偶数位节点及后序节点不为空，可以继续循环
    while (even != null && even.next != null) {
        // 3.1 奇数位节点指针连接偶数位节点的后一个
        odd.next = even.next;
        // 3.2 奇数位指针到下一个奇数位节点
        odd = odd.next;
        // 3.3 偶数位指针节点连接奇数位节点的后一个
        even.next = odd.next;
        // 3.4 偶数位指针进入下一个偶数位节点
        even = even.next;
    }
    // 4. 偶数位节点的头连在奇数位链表尾节点的后面
    odd.next = evenPivot;
    return head;
}
时间复杂度

\(O(n)\)

遍历一次链表所有节点。

空间复杂度

\(O(1)\)

常数级指针变量，没有额外辅助空间。

BM11 链表相加(二)

描述

假设链表中每一个节点的值都在 0 - 9 之间，那么链表整体就可以代表一个整数。

给定两个这种链表，请生成代表两个整数相加值的结果链表。

例如：链表 1 为 9->3->7，链表 2 为 6->3，最后生成新的结果链表为 1->0->0->0。

示例

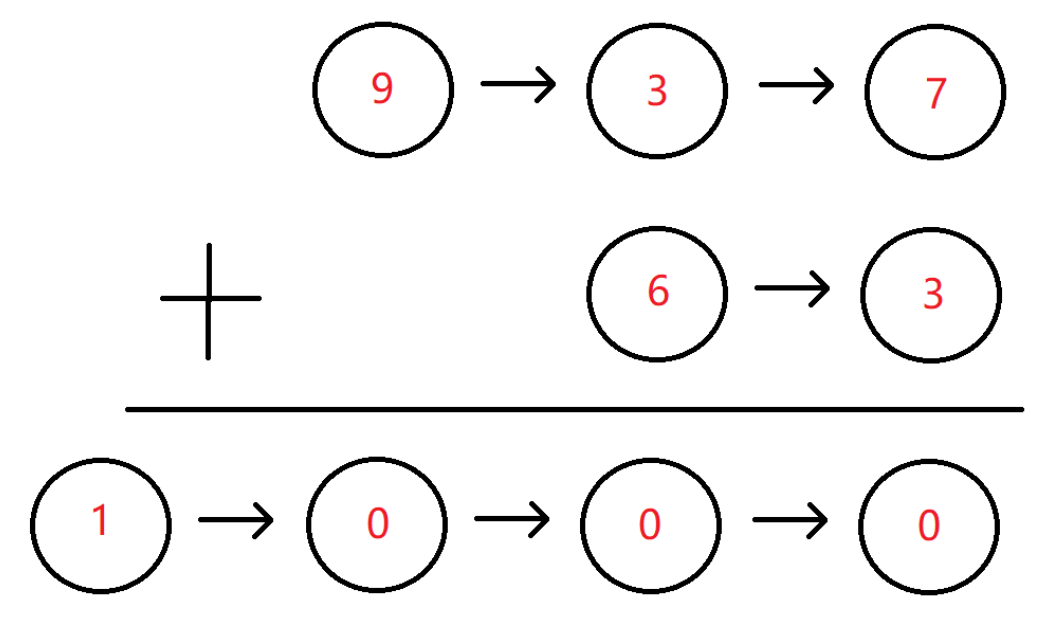
F1：反转链表

思路

链表无法逆序遍历，我们可以将两个链表都反转，然后进行相加运算。

步骤
  1. 任意一个链表为空，返回另一个链表即可，因为链表为空相当于 0。
  2. 反转两个待相加的链表。
  3. 设置返回链表的链表头，设置进位 carry = 0。
  4. 从头开始遍历两个链表，直到两个链表节点都为空且 carry 也不为 1。每次取出不为空的链表节点值，为空就设置为 0，将两个数字与 carry 相加，然后查看是否进位，将进位后的结果（对 10 取模）加入新的链表节点，连接在返回链表的后面，并继续向后遍历。
  5. 返回前将结果链表再反转回来。
链表相加
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
public ListNode addInList(ListNode head1, ListNode head2) {
    // 1. 任意一个链表为空，返回另一个
    if (head1 == null)
        return head2;
    if (head2 == null)
       return head1;
    // 2. 反转两个链表
    head1 = reverse(head1);
    head2 = reverse(head2);
    // 3. 添加表头，设置进位
    ListNode ans = new ListNode(-1);
    ListNode pivot = ans;
    int carry = 0; // 进位
    // 4. 只要某个链表不为空，或者还有进位
    while (head1 != null || head2 != null || carry != 0) {
        // 链表不为空则取其值，否则设为 0
        int val1 = head1 == null ? 0 : head1.val;
        int val2 = head2 == null ? 0 : head2.val;
        // 相加
        int sum = val1 + val2 + carry;
        // 获取进位
        carry = sum / 10;
        // 获取节点值
        sum %= 10;
        // 结果链表添加节点
        pivot.next = new ListNode(sum);
        pivot = pivot.next;
        // 待相加链表节点不为空，则向下移动
        if (head1 != null) {
            head1 = head1.next;
        }
        if (head2 != null) {
            head2 = head2.next;
        }
    }
    return reverse(ans.next);
}
public ListNode reverse(ListNode head) {
    if (head == null)
        return head;
    ListNode pre = null;
    ListNode cur = head;
    ListNode next = null;
    while (cur != null) {
        next = cur.next;
        cur.next = pre;
        pre = cur;
        cur = next;
    }
    return pre;
}
时间复杂度

\(O(max(m,n))\)

其中 m 与 n 分别为两个链表的长度，反转链表三次，复杂度分别为 \(O(n)\)、\(O(m)\)、\(O(max(m,n))\)，相加过程也是遍历较长的链表。

空间复杂度

\(O(1)\)

常数级指针变量，没有额外辅助空间，返回的新链表属于必要空间。

BM12 单链表的排序

描述

给定一个节点数为n的无序单链表，对其按升序排序。

F1：归并排序

思路

如何合并呢？

在合并阶段可以参考 BM4 合并两个有序链表，两个链表逐渐取最小的元素即可。

如何划分呢？

常规数组的归并排序是分治思想，即将数组从中间元素开始划分，然后将划分后的子数组作为一个要排序的数组，再将排好序的两个子数组合并成一个完整的有序数组，因此采用的是递归。

在链表中，我们也可以使用同样的方式，只需找到中间节点的前一个节点，将其断开，就可以将链表分成两个子链表，然后继续划分，直到最小，然后向上依次合并。

  • 终止条件：当子链表划分到为空或者只剩一个节点时，不再继续划分，向上合并。
  • 返回值：每次返回两个排好序且合并好的子链表。
  • 本级任务：找到这个链表的中间节点，从前面断开，分为左右两个子链表，进入子问题排序。

如何找中间节点呢？

可以参靠 BM13 判断一个链表是否是回文结构 的方法 2 双指针寻中法，快指针每次两步，慢指针每次一步，当快指针到达链表尾的时候，慢指针正好走了快指针距离的一半，为中间节点。

步骤
  1. 首先判断链表为空或者只有一个元素，直接就是有序的。
  2. 准备三个指针，快指针 right 每次走两步，慢指针 mid 每次走一步，前序指针 left 每次跟在 mid 前一个位置。三个指针遍历链表，当快指针到达链表尾部的时候，慢指针刚好走了链表的一半，正好是中间位置。
  3. 从 left 位置将链表断开，刚好分成两个子问题开始递归。
  4. 将子问题得到的链表合并。
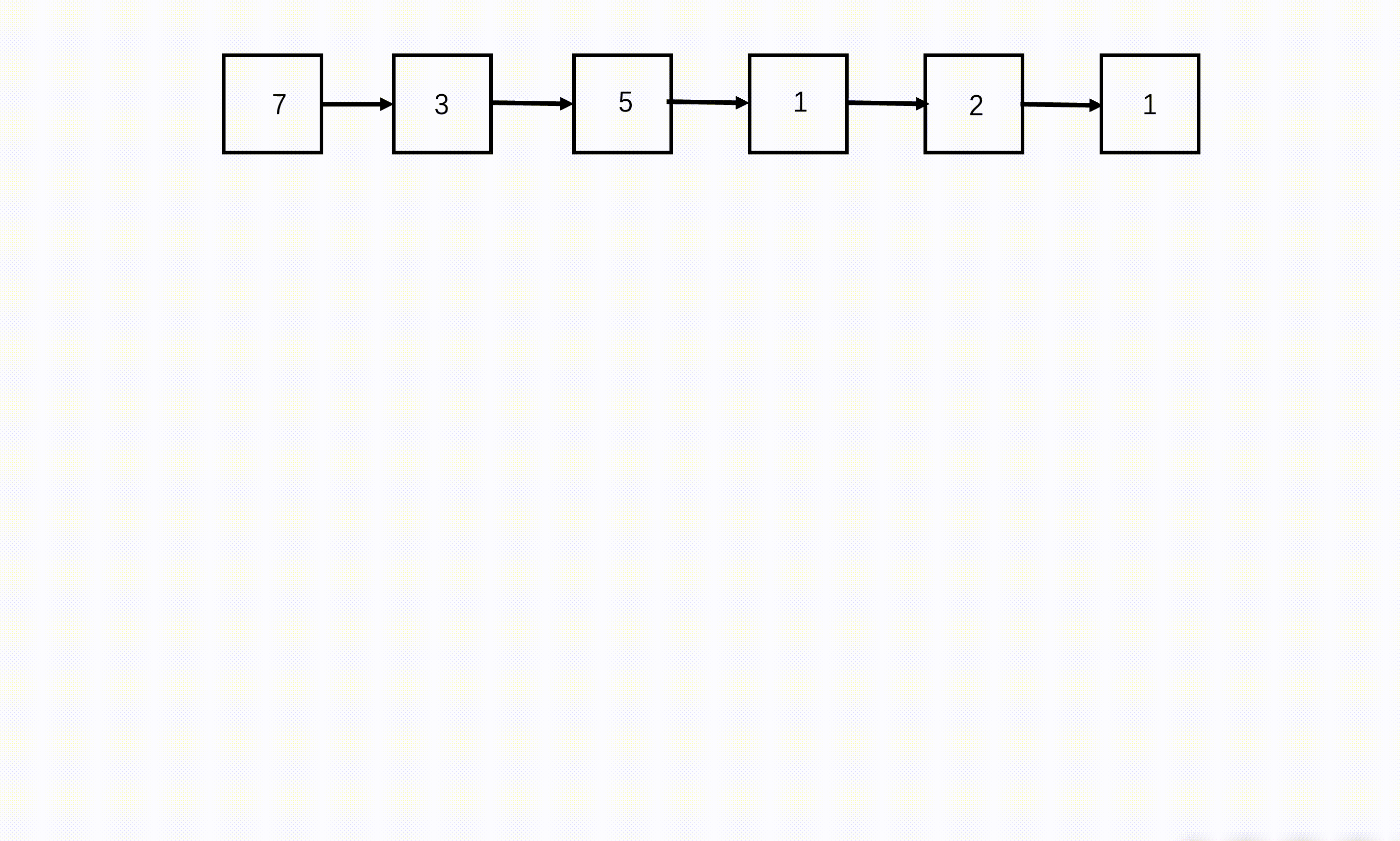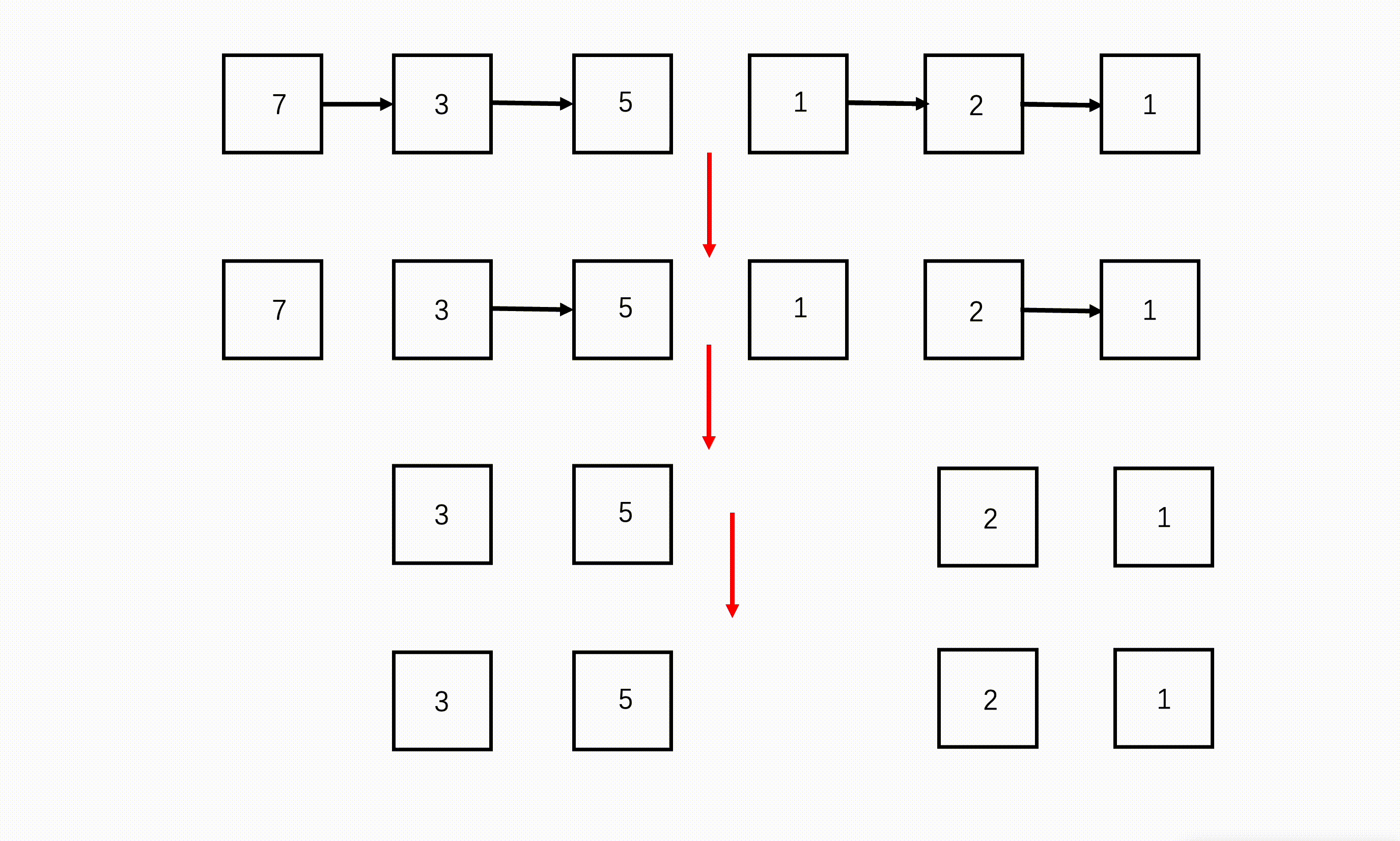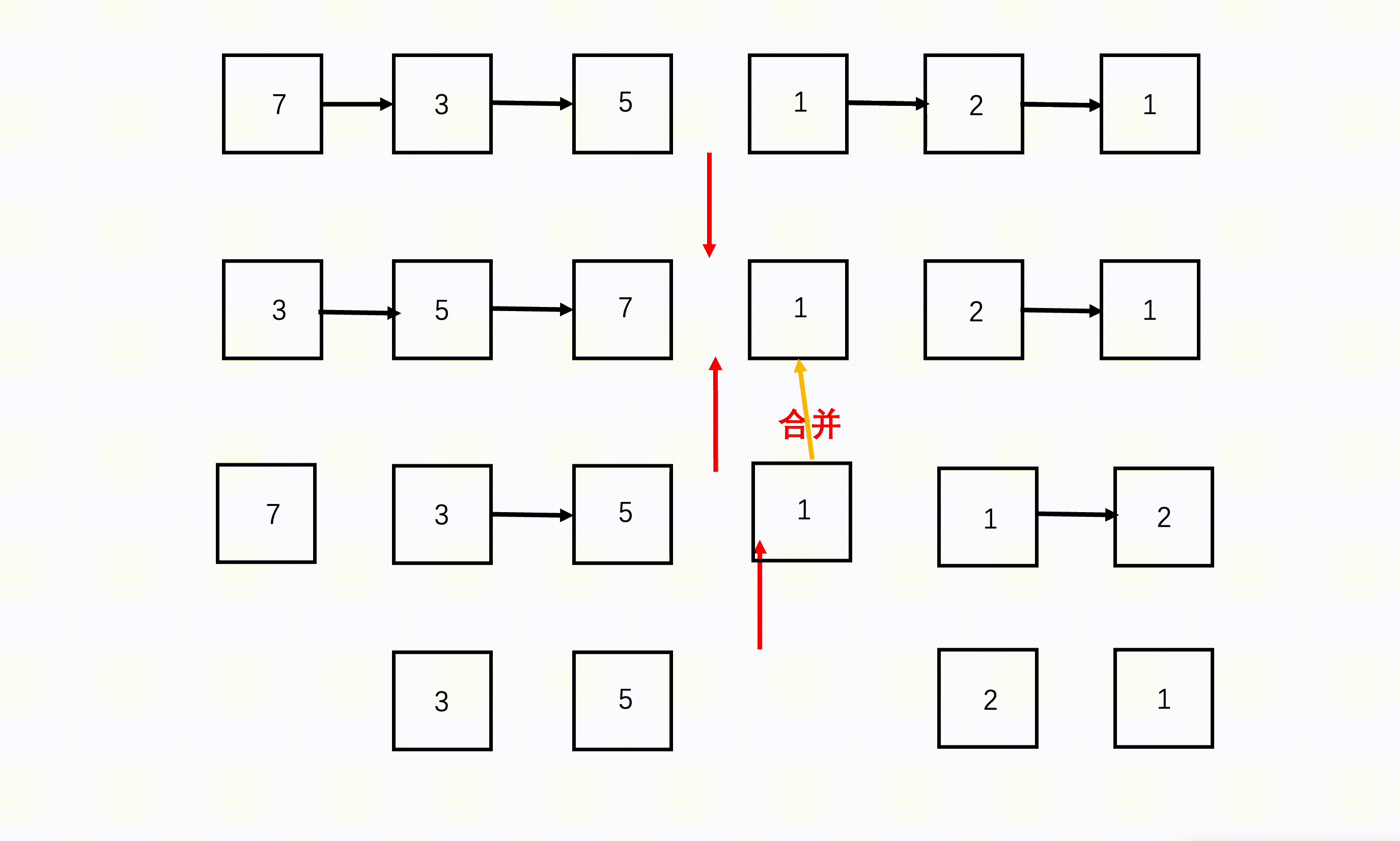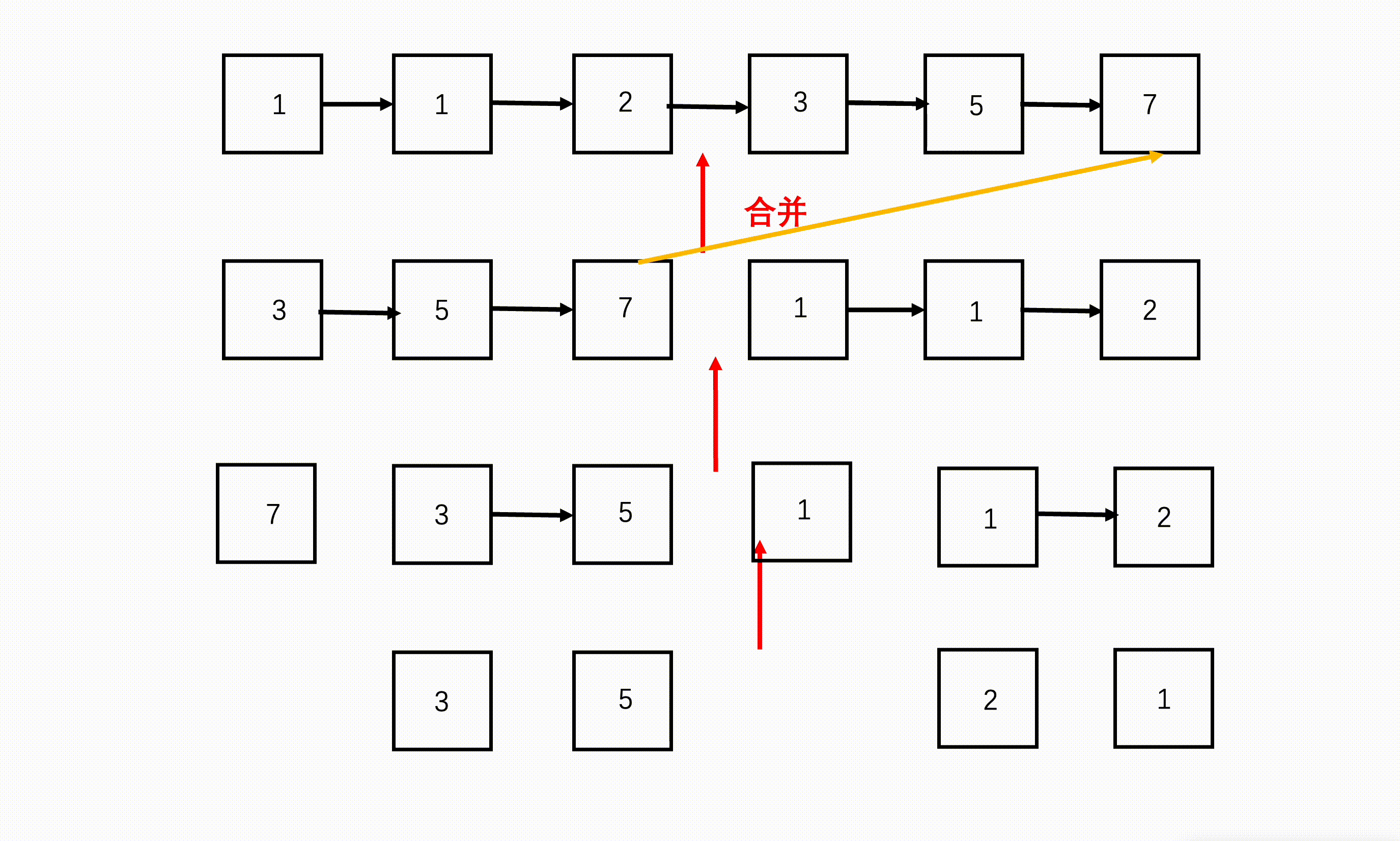
双指针归并完成单链表升序
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
public ListNode sortInList(ListNode head) {
    // 链表为空或只有一个元素，直接就是有序的，返回即可。
    if (head == null || head.next == null)
        return head;
    // 构建三个指针
    ListNode left = head;
    ListNode mid = head.next;
    ListNode right = head.next.next;
    // 右边的指针到达链表终点时，中间的指针指向该段链表的中间节点
    while (right != null && right.next != null) {
        right = right.next.next;
        mid = mid.next;
        left = left.next;
    }
    // 中间指针的前序指针指向左段的最后一个节点，从这里断开
    left.next = null;
    // 分成两段排序，合并排好序的两段
    return merge(sortInList(head), sortInList(mid));
}

// 合并两个有序链表
public ListNode merge(ListNode list1, ListNode list2) {
    // 一个链表为空，直接返回另一个
    if (list1 == null)
        return list2;
    if (list2 == null)
        return list1;
    // 添加一个表头
    ListNode pivot = new ListNode(-1);
    ListNode cur = pivot;
    // 两个链表都不能为空
    while (list1 != null && list2 != null) {
        // 取较小值的节点
        if (list1.val <= list2.val) {
            cur.next = list1;
            // 只移动取了值的指针
            list1 = list1.next;
        } else {
            cur.next = list2;
            // 只移动取了值的指针
            list2 = list2.next;
        }
        // 指针后移
        cur = cur.next;
    }
    // 哪个链表还剩，直接连在后面
    if (list1 != null)
        cur.next = list1;
    else
        cur.next = list2;
    // 返回值去掉表头
    return pivot.next;
}
时间复杂度

\(O(nlog_2n)\)

每一级划分最坏需要遍历链表全部元素，因此 \(O(n)\)，每一级合并都是将同级的子问题链表遍历合并，因此也为 \(O(n)\)，分治划分为二叉树型，一共有 \(O(log_2n)\) 层，因此复杂度为 \(O((n + n) * log_2n)\) = \(O(nlog_2n)\)

空间复杂度

\(O(log_2n)\)

递归栈的深度最坏为树形递归的深度，\(log_2n\) 层。

F2：转化为数组排序

思路

链表无法按照下标访问，只能逐个遍历，因此像排序中的快速排序、堆排序都无法使用，只能使用一次遍历的冒泡排序、选择排序这些。但是这些 \(O(n^2)\) 复杂度的排序方法太费时间了，我们可以将其转化成数组后再排序。

步骤
  1. 遍历链表，将节点值加入数组。
  2. 使用内置的排序函数对数组进行排序。
  3. 依次遍历数组和链表，按照位置将链表中的节点值修改为排序后的数组值。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public ListNode sortInList(ListNode head) {
    ArrayList<Integer> nums = new ArrayList<>();
    ListNode p = head;
    // 遍历链表，将节点值加入数组
    while (p != null) {
        nums.add(p.val);
        p = p.next;
    }
    p = head; // 重置下标
    // 对数组排序
    Collections.sort(nums);
    // 遍历数组
    for (int i = 0; i < nums.size(); i++) {
        p.val = nums.get(i);
        p = p.next;
    }
    return head;
}
时间复杂度

\(O(nlog_2n)\)

sort 函数一般为优化后的快速排序，复杂度为 \(O(nlog_2n)\)。

空间复杂度

\(O(n)\)

存储链表元素值的辅助数组长度 n。