双指针巧解链表有环问题

发表于 更新于 分类于 ， 本文字数： 1.2k 阅读时长 ≈ 4 分钟 阅读次数：

链表有环问题可以使用双指针技巧轻松解决。

  • 判断链表是否有环问题，可以通过设置快慢指针同向遍历链表，若相遇则有环。

  • 找环入口问题，也可以通过设置快慢指针同向遍历链表，寻找相遇点。不同的是，当两指针相遇后，快指针回到链表头节点，慢指针留在相遇节点，两者同速遍历，二次相遇点一定是环入口。

下面两道题精选于牛客网面试必刷TOP101，相信我，十分简单，非常容易理解！

BM6 判断链表中是否有环

描述

判断给定的链表中是否有环。如果有环则返回 true，否则返回 false。

思路

双指针

线性与环形链表特点：

  • 线性链表末尾一定有 null。

  • 环形链表的环一定在末尾，末尾没有 null 了。

线性与环形链表结束条件：

  • 线性链表的结束条件就是遍历到 null。

  • 环形链表会不断循环，需要借助双指针才能结束。同向访问的双指针，因为速度不同，只要有环，二者一定能相遇。

F1：双指针

步骤
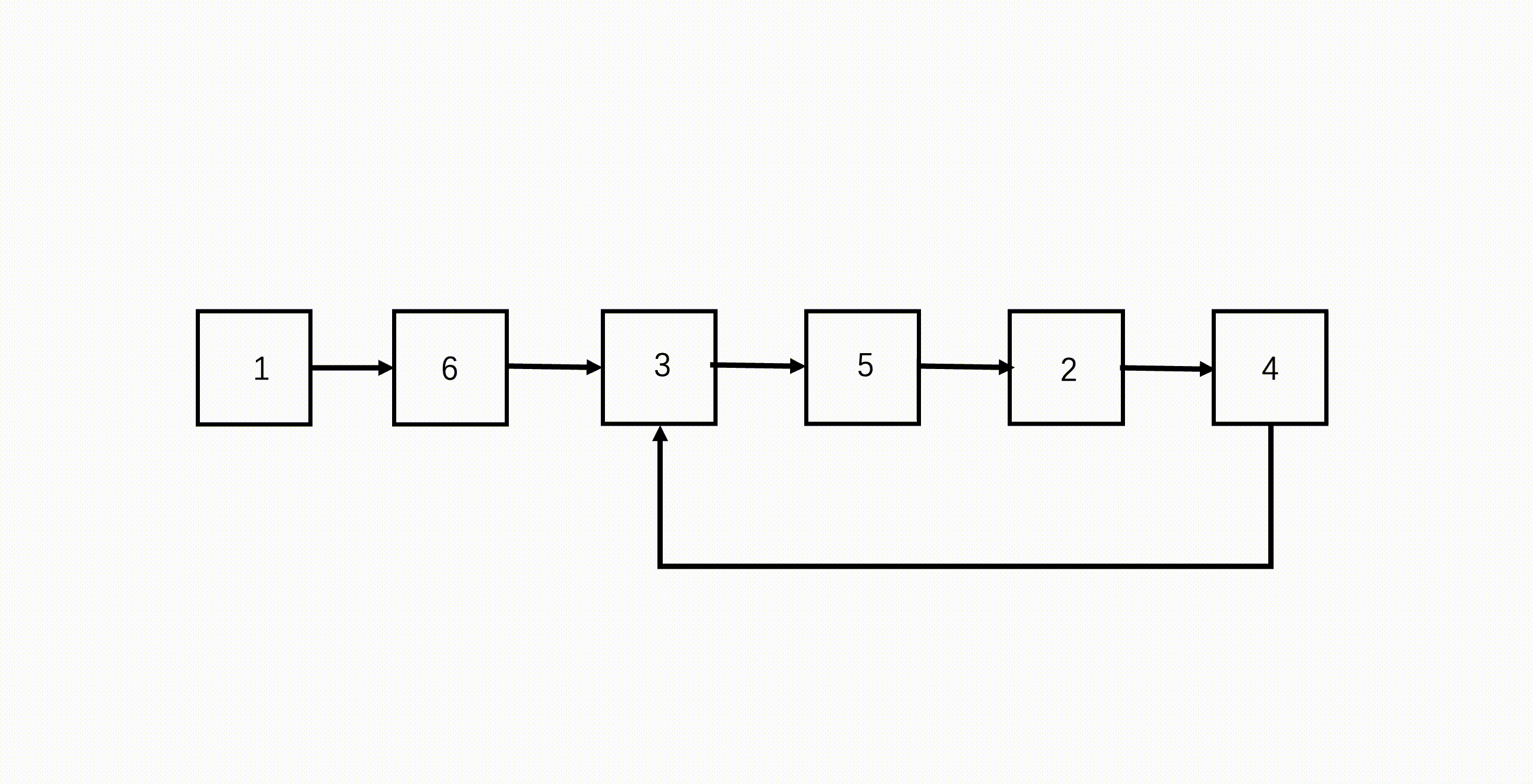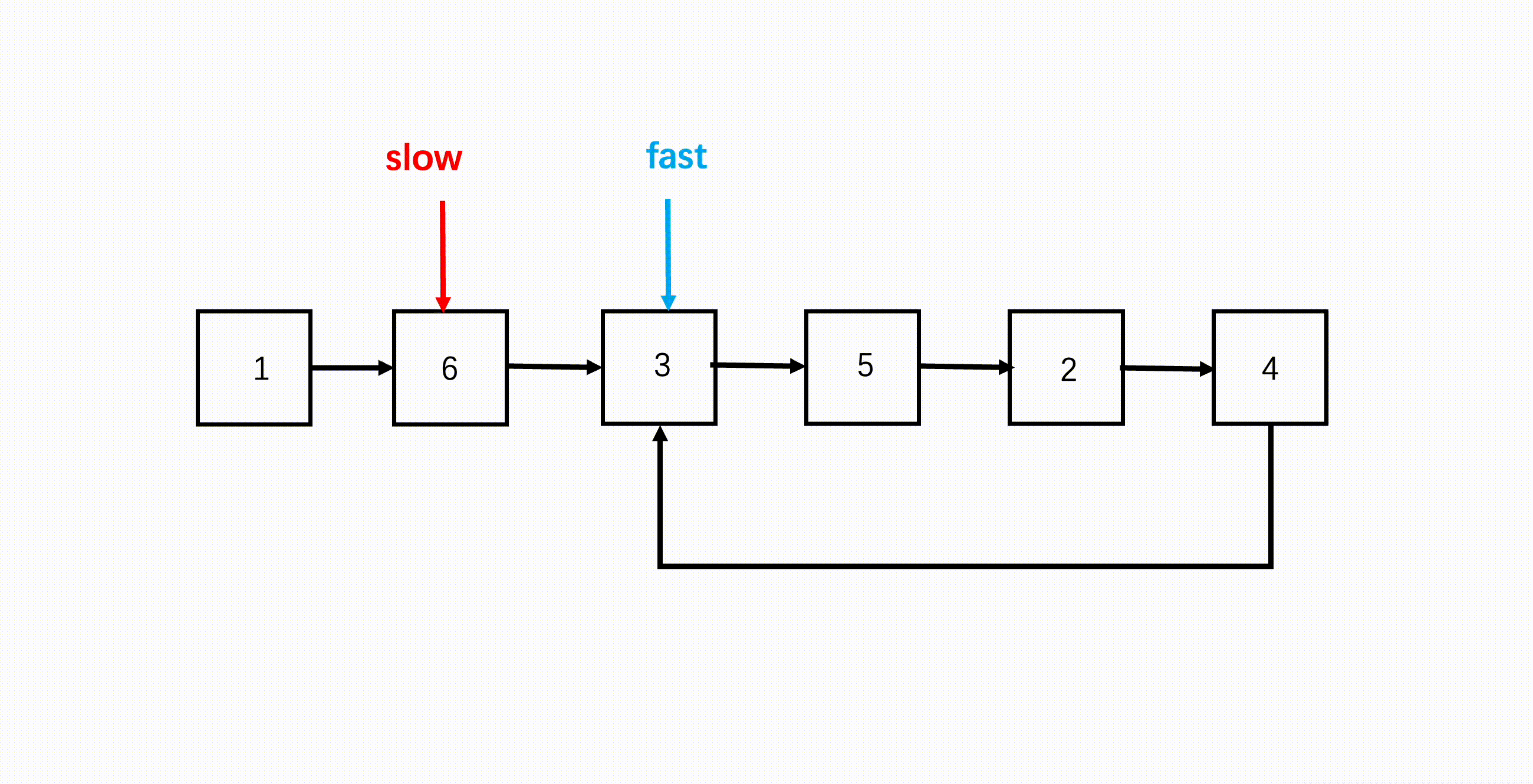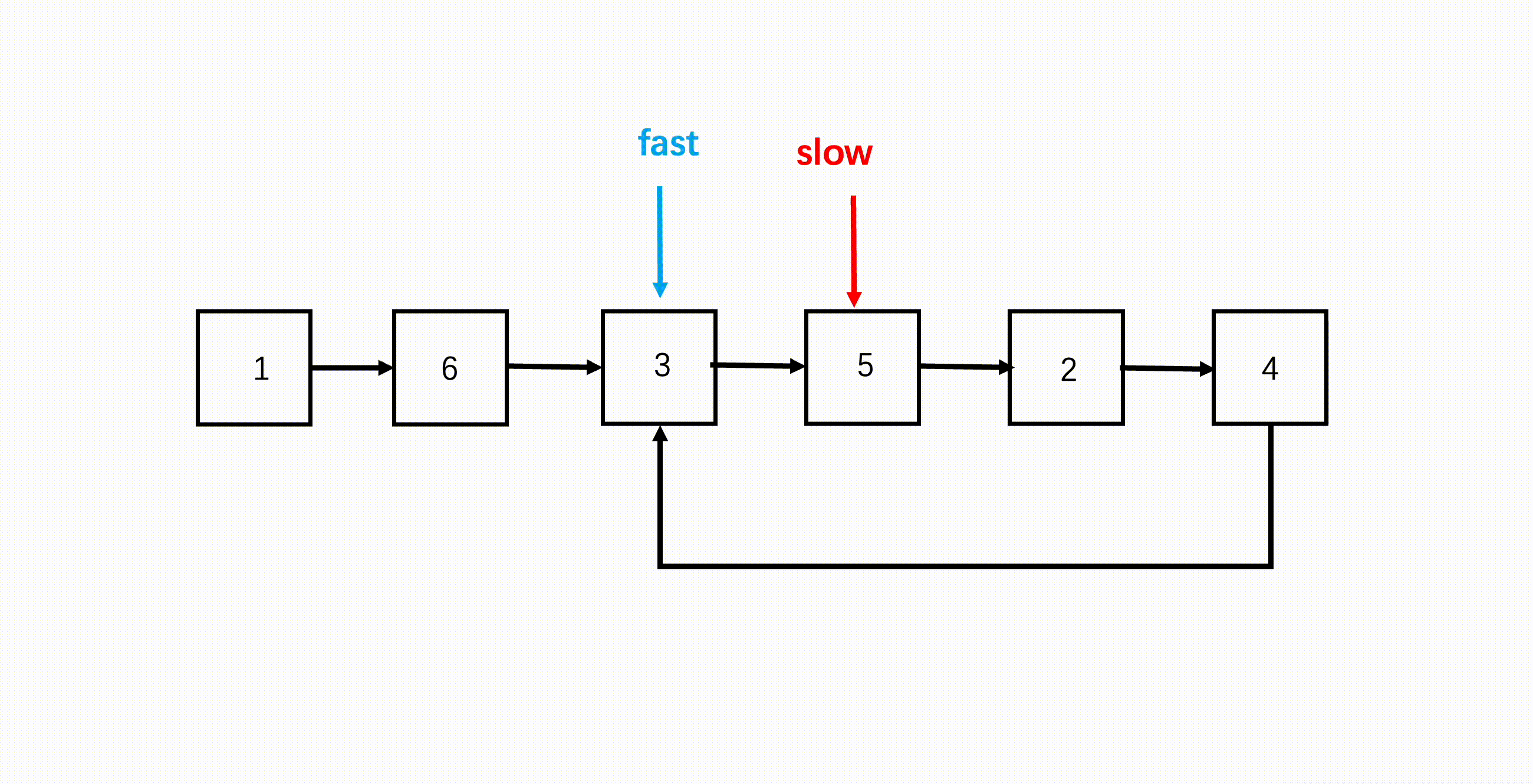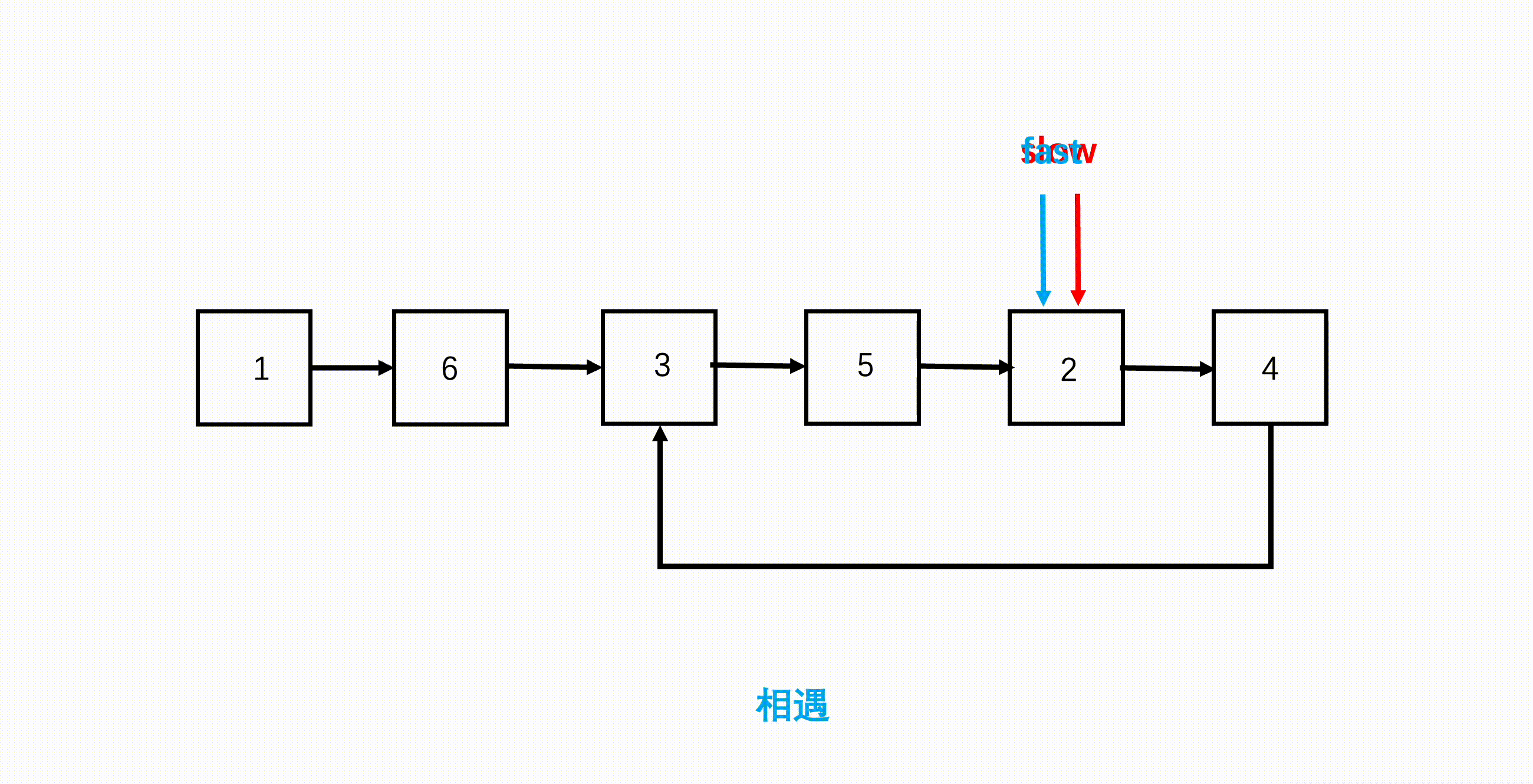
  1. 设置快慢两指针，初始都指向链表头；
  2. 遍历链表，快指针每次走两步，慢指针每次走一步；
  3. 如果快指针到了链表末尾，说明没有环，因为它每次走两步，所以要验证连续两步是否为 null；
  4. 如果链表有环，那快慢双指针会在环内循环，因为快指针每次走两步，因此快指针会在环内追到慢指针，二者相遇就代表有环。
双指针判断链表是否有环
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public boolean hasCycle(ListNode head) {
    // 先判断链表为空的情况
    if (head == null)
        return false;
    // 1. 设置快慢两指针，初始都指向链表头
    ListNode fast = head;
    ListNode slow = head;
    // 2. 遍历链表
    // 3. 如果没环，fast 会先到链表尾
    while (fast != null && fast.next != null) {
        // 快指针移动两步
        fast = fast.next.next;
        // 慢指针移动一步
        slow = slow.next;
        // 相遇则有环
        if (fast == slow)
            return true;
    }
    // 到末尾，则没有环
    return false;
}
时间复杂度

\(O(M)\)

最坏情况下遍历链表 n 个节点。

空间复杂度

\(O(1)\)

仅使用了两个指针，没有额外辅助空间。

BM7 链表中环的入口点

描述

给一个长度为 n 链表，若其中包含环，请找出该链表的环的入口结点，否则，返回 null。

分解任务
  1. 判断链表是否有环；
  2. 在有环的链表中找到环的入口。

思路

双指针

如何找到环的入口

一个有环链表。

假设快指针在环中走了 \(n\) 圈，慢指针走了 \(m\) 圈，两者相遇。

链表头节点到环入口点距离为 \(x\)，环入口到相遇点距离为 \(y\)，相遇点到环入口点距离为 \(z\)。

快指针一共走了 \(x + n(y + z) + y\) 步，慢指针一共走了 \(x + m(y + z) + y\) 步。

快指针走的步数是慢指针的两倍，则 \[ x + n(y + z) + y = 2(x + m(y + z) + y) \] 进一步推导， \[ x+y=(n-2m)(y+z) \] 因为环的大小是 \(y+z\)，说明从链表头经过环入口到达相遇地方经过的距离等于整数倍环的大小。那么，我们从头开始遍历到相遇位置，和从相遇位置开始在环中遍历，会使用相同的步数，而双方最后都会经过入口到相遇位置这 \(y\) 个节点，说明这 \(y\) 个节点它们就是重叠遍历的，那它们从入口位置就相遇了，这样就找到了入口节点。

F1：双指针

步骤
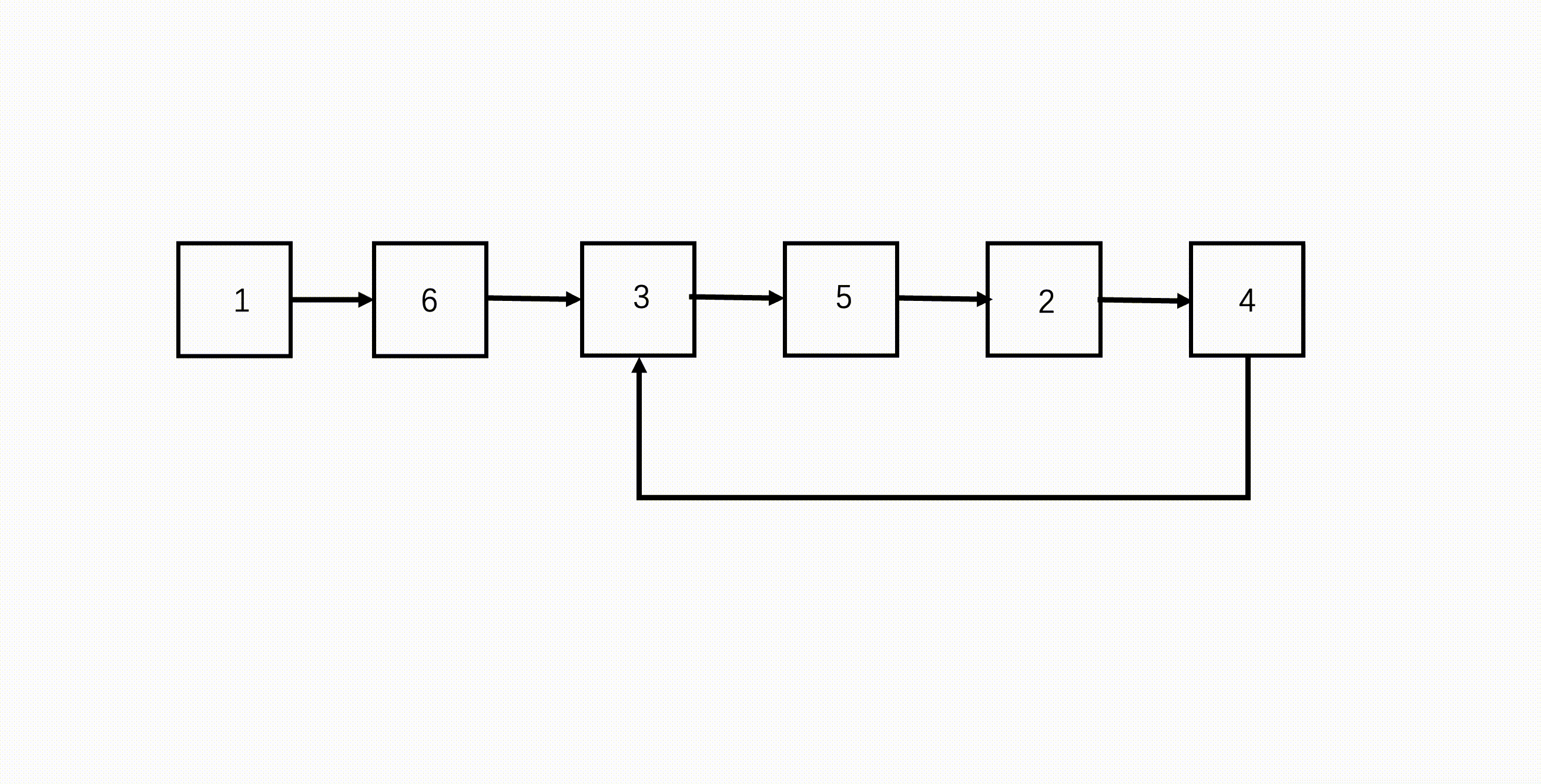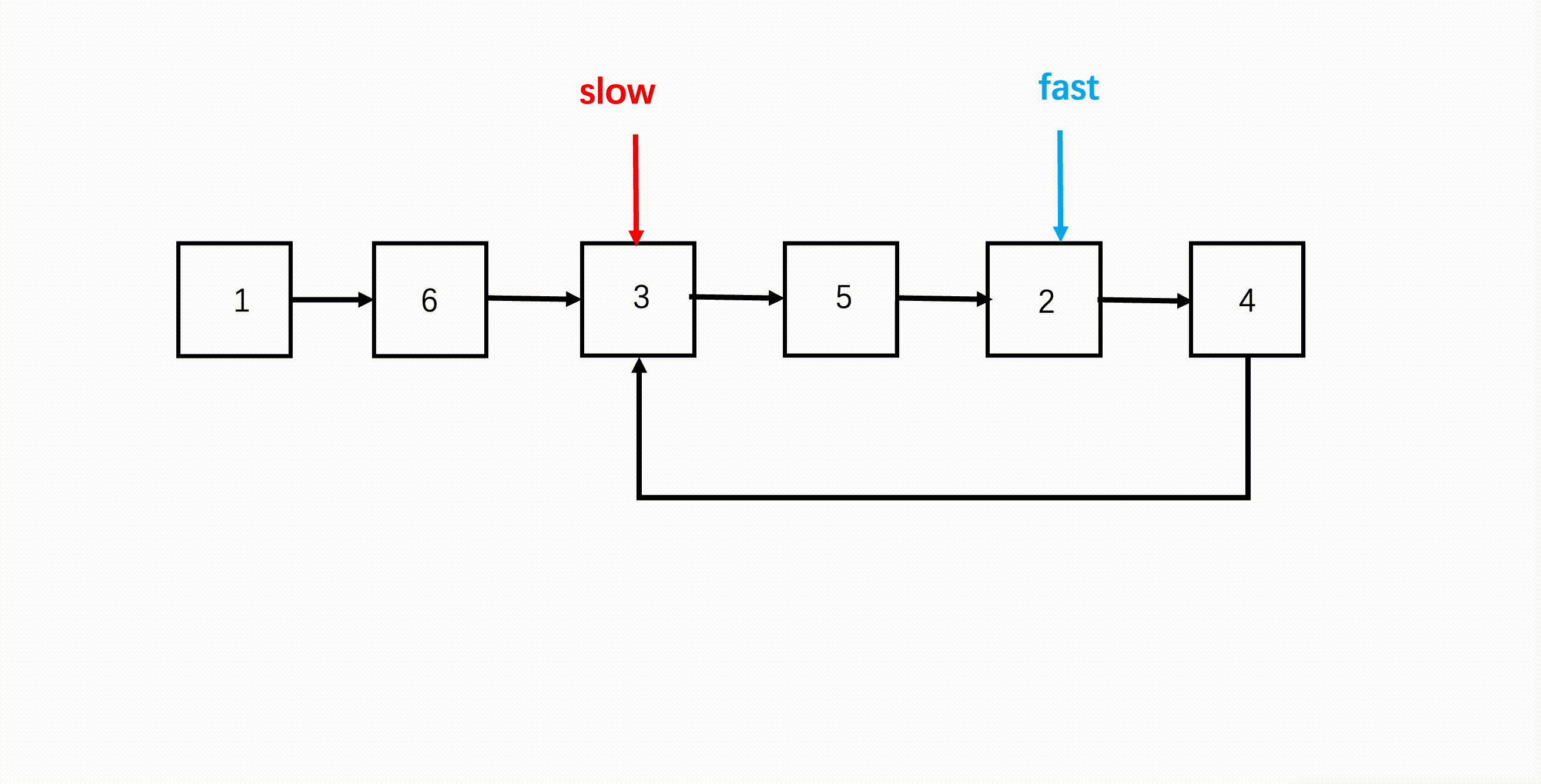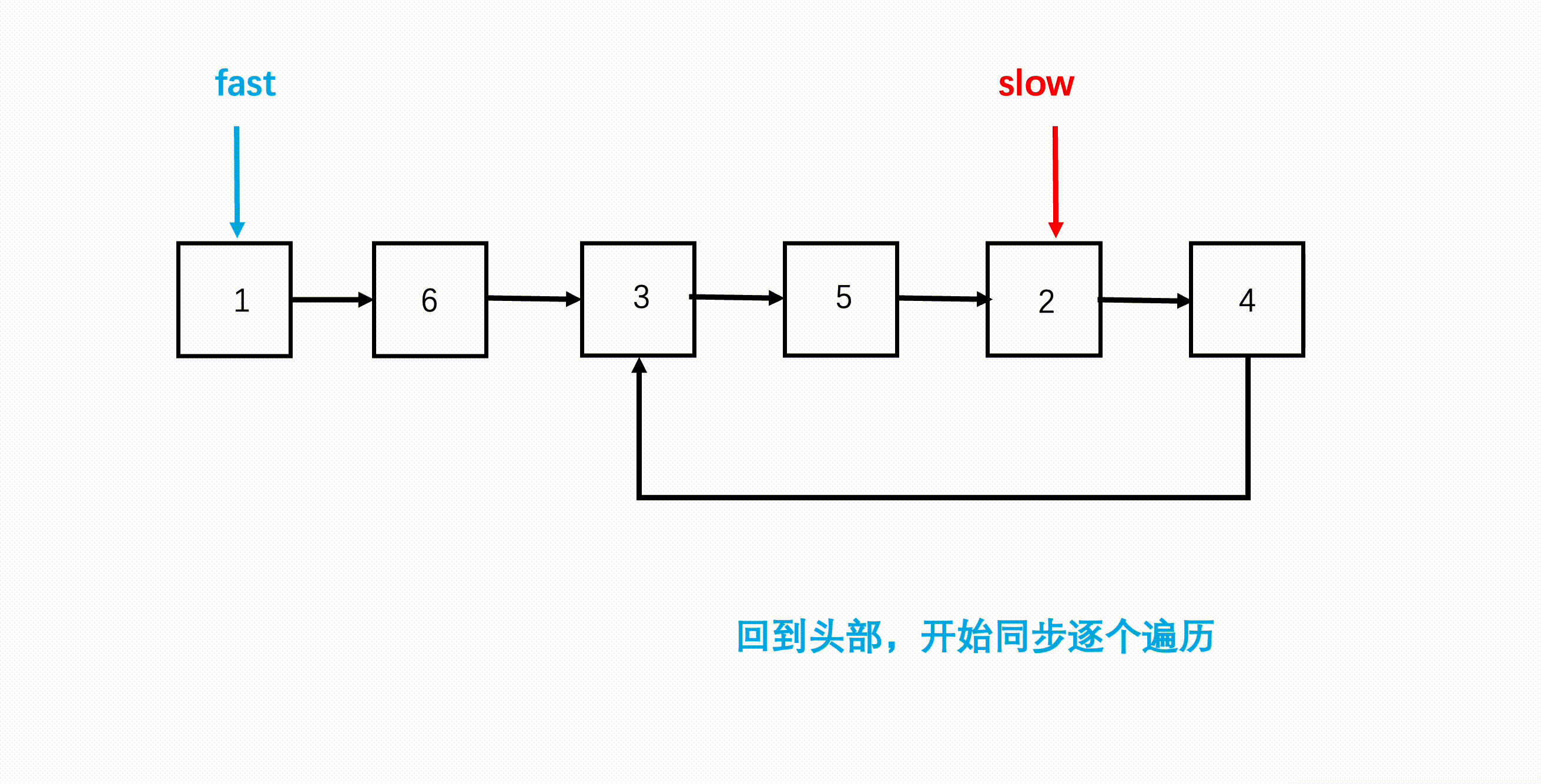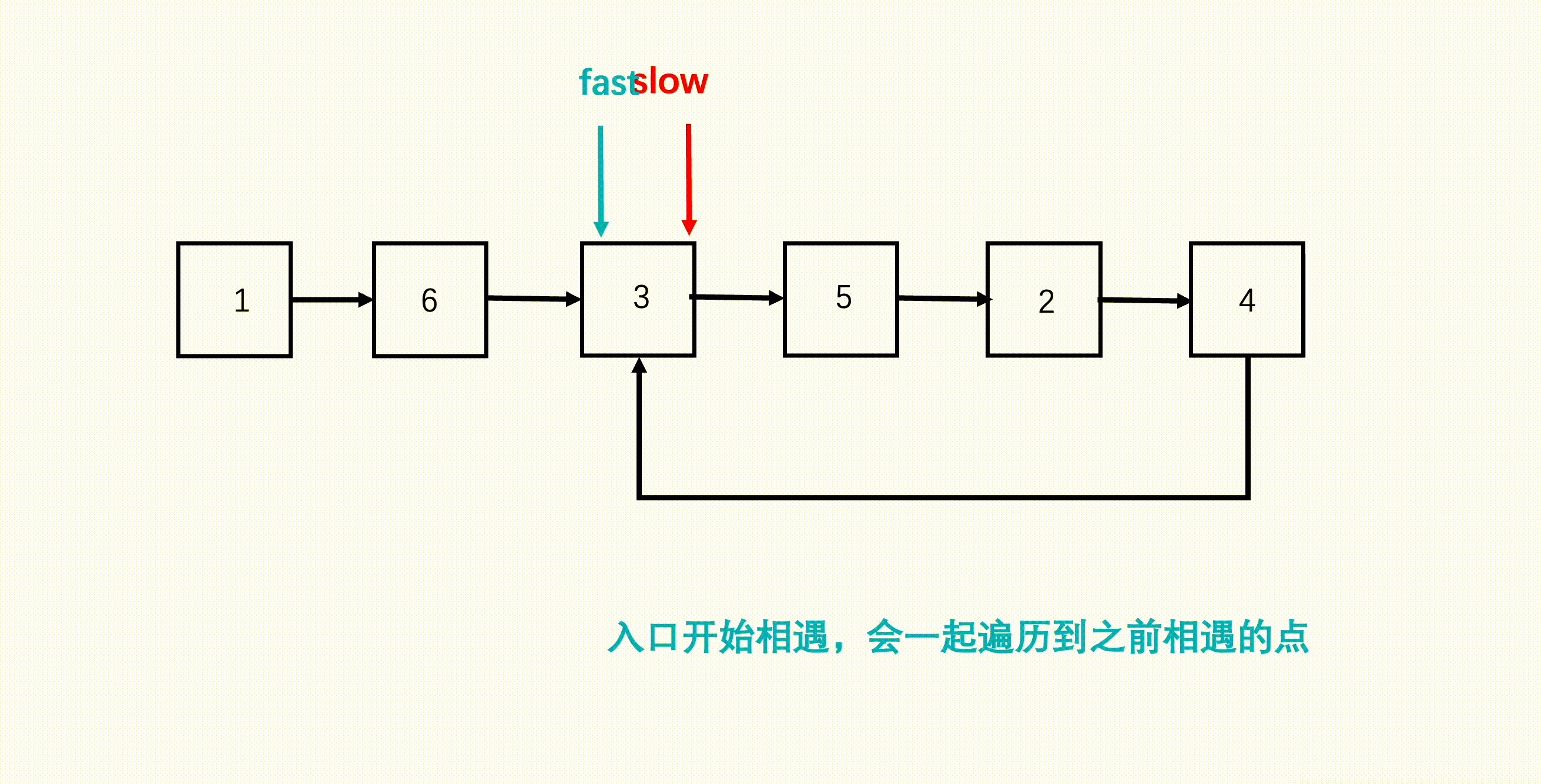
  1. 使用 BM6 方法判断链表是否有环，并找到相遇节点。
  2. 慢指针继续在相遇节点，快指针回到链表头，两个指针同步逐个元素开始遍历链表。
  3. 两者再次相遇的地方就是环的入口。
双指针找环入口问题
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// 寻找链表中环的入口节点
public ListNode entryNodeOfLoop(ListNode pHead) {
    ListNode slow = hasCycle(pHead);
    // 没有环
    if (slow == null)
        return null;
    // 有环
    // 快指针回到表头
    ListNode fast = pHead;
    // 再次相遇即是环入口
    while (fast != slow) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}

// 判断有没有环
public ListNode hasCycle(ListNode head) {
    // 先判断链表为空的情况
    if (head == null)
        return null;
    // 快慢双指针
    ListNode fast = head;
    ListNode slow = head;
    // 如果没环，快指针会先到链表尾
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        // 相遇则有环，返回相遇的节点
        if (slow == fast) {
            return slow;
        }
    }
    // 到末尾说明没有换，返回 null
    return null;
}
时间复杂度

\(O(n)\)

最坏情况下遍历链表两次

空间复杂度

\(O(1)\)

使用了常数个指针，没有额外辅助空间