手撕算法必备技巧（贰） —— 双指针（链表篇）

发表于 更新于 分类于 ， 本文字数： 6.9k 阅读时长 ≈ 25 分钟 阅读次数：

本文介绍了双指针技巧在链表、数组以及字符串中的使用，给出了大量大厂常见面试手撕题目的思路及代码，不仅适合完全不了解双指针技巧的读者，也适合老司机复习拓展。

考察过该技巧的公司有阿里巴巴、腾讯、美团、拼多多、百度、华为等大厂。

我相信，友好的讨论交流会让彼此快速进步！文章难免有疏漏之处，十分欢迎大家在评论区中批评指正。

食用指南： ⭐️为一刷必做题，便于快速理解双指针技巧；无星题目可在刷完⭐️题目后再做，用于拓展学习双指针技巧如何与其他算法知识结合使用。

日志更新：文章底部给出了更新日志，帮助小伙伴们快速知晓最近优化了哪些技巧，更新了哪些题目。

我相信，友好的讨论交流会让彼此快速进步！文章难免有疏漏之处，十分欢迎大家在评论区中批评指正。

双指针技巧是什么？

双指针技巧指的就是在遍历链表、数组或者字符串的过程中，不是使用一个指针来进行访问，而是使用两个指针（甚至可以多个，合并 k 个有序链表中将会用到）进行遍历访问。

以链表为例，两个指针要么同方向访问两个链表、要么同方向访问一个链表（快慢指针）、要么相反方向遍历一个链表（左右指针），数组和字符串也是如此。

下面，先来看看双指针技巧在链表问题中的应用。我们以题目入手，从易到难，逐步感受双指针技巧的精妙之处。

几乎所有题目都提供了使用双指针技巧的思路，以及动画示意图，希望可以通过这一篇文章让你彻底弄懂双指针技巧。

合并与分割类问题

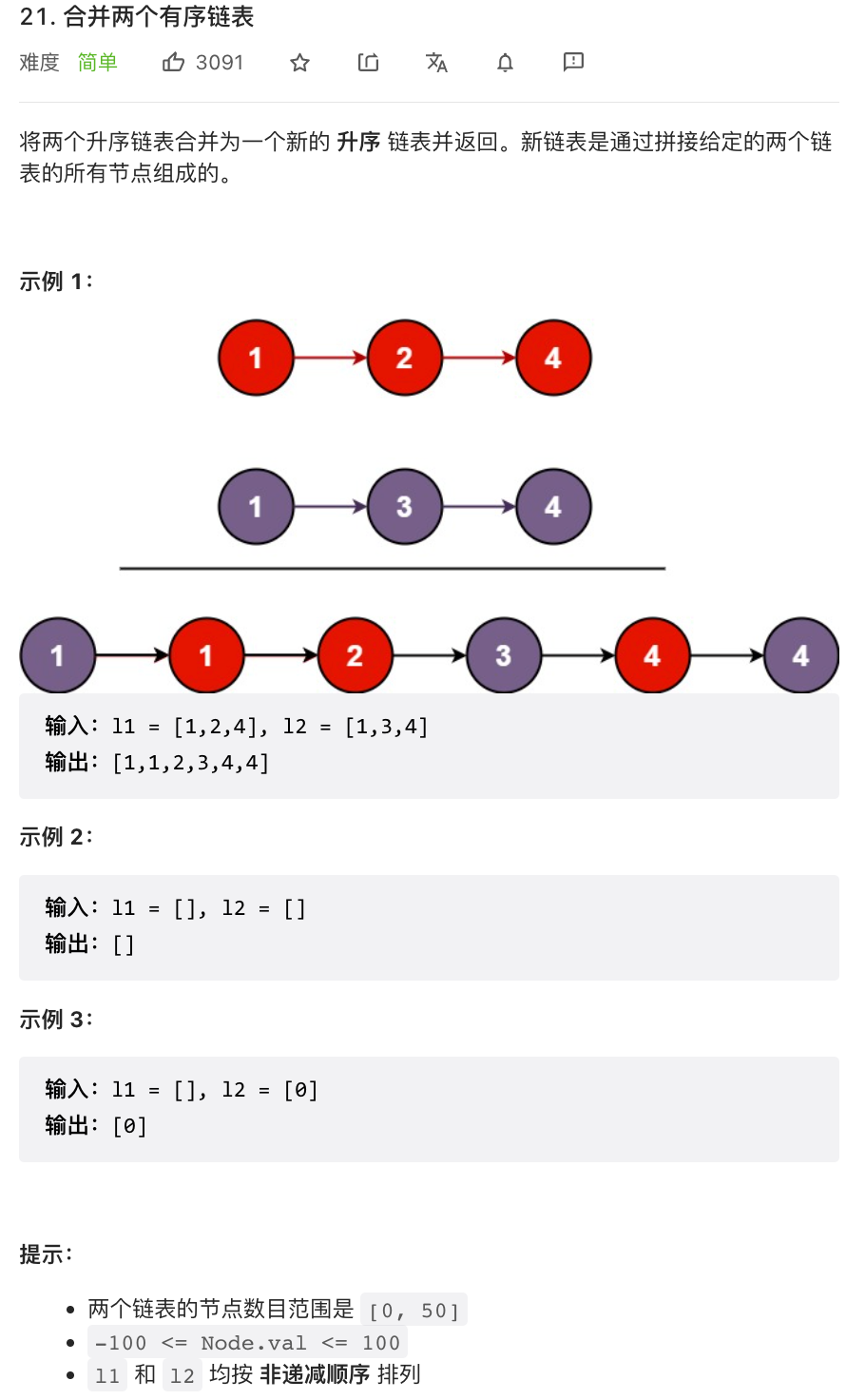
⭐️合并两个有序链表(力扣21)

题目描述

力扣-21-合并两个有序链表

思路(双指针)

题目中两个链表已经排好序，我们可以使用两个指针同向访问两个链表，每次比较两个指针的元素，谁小谁加到新的链表上。

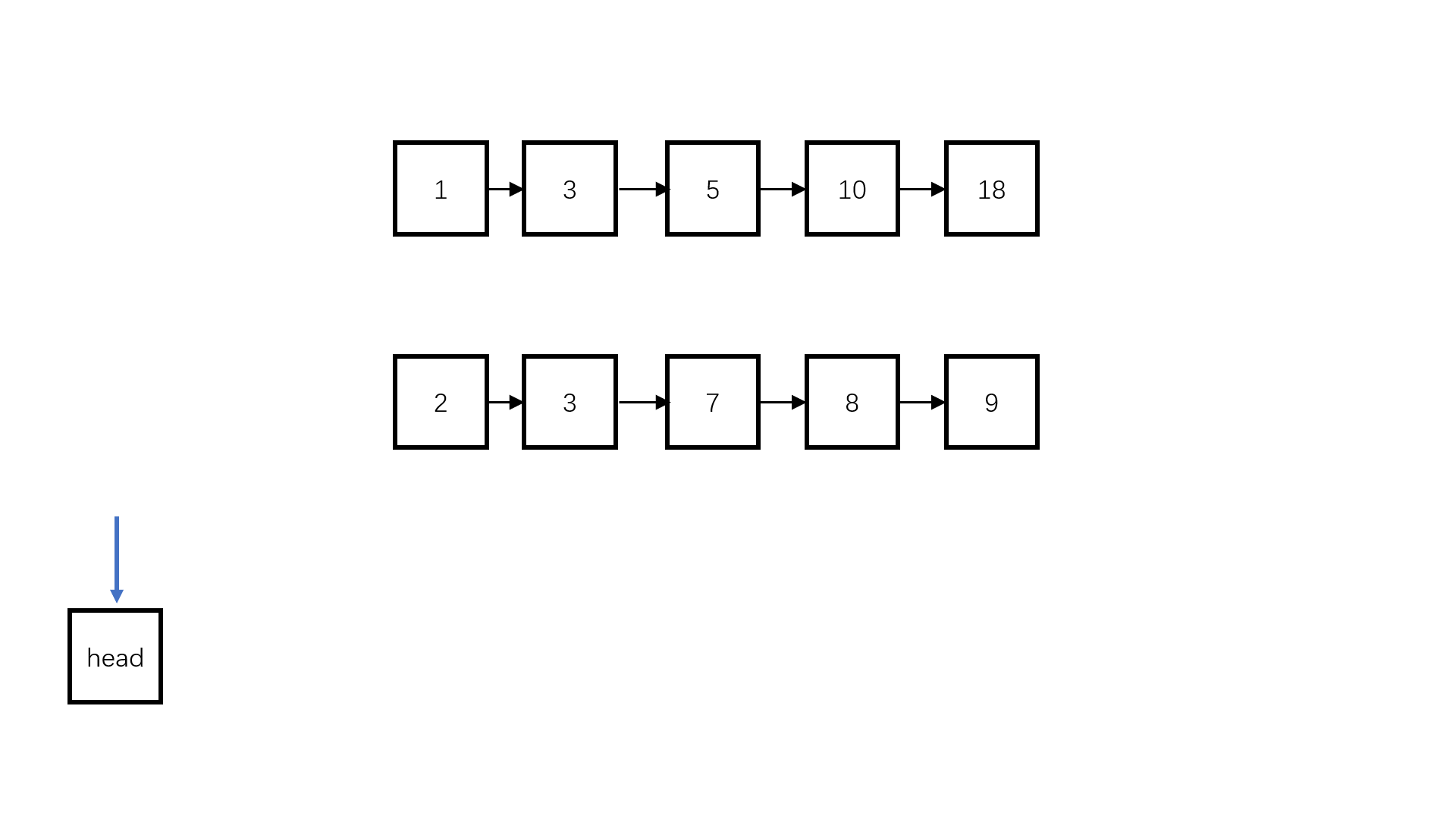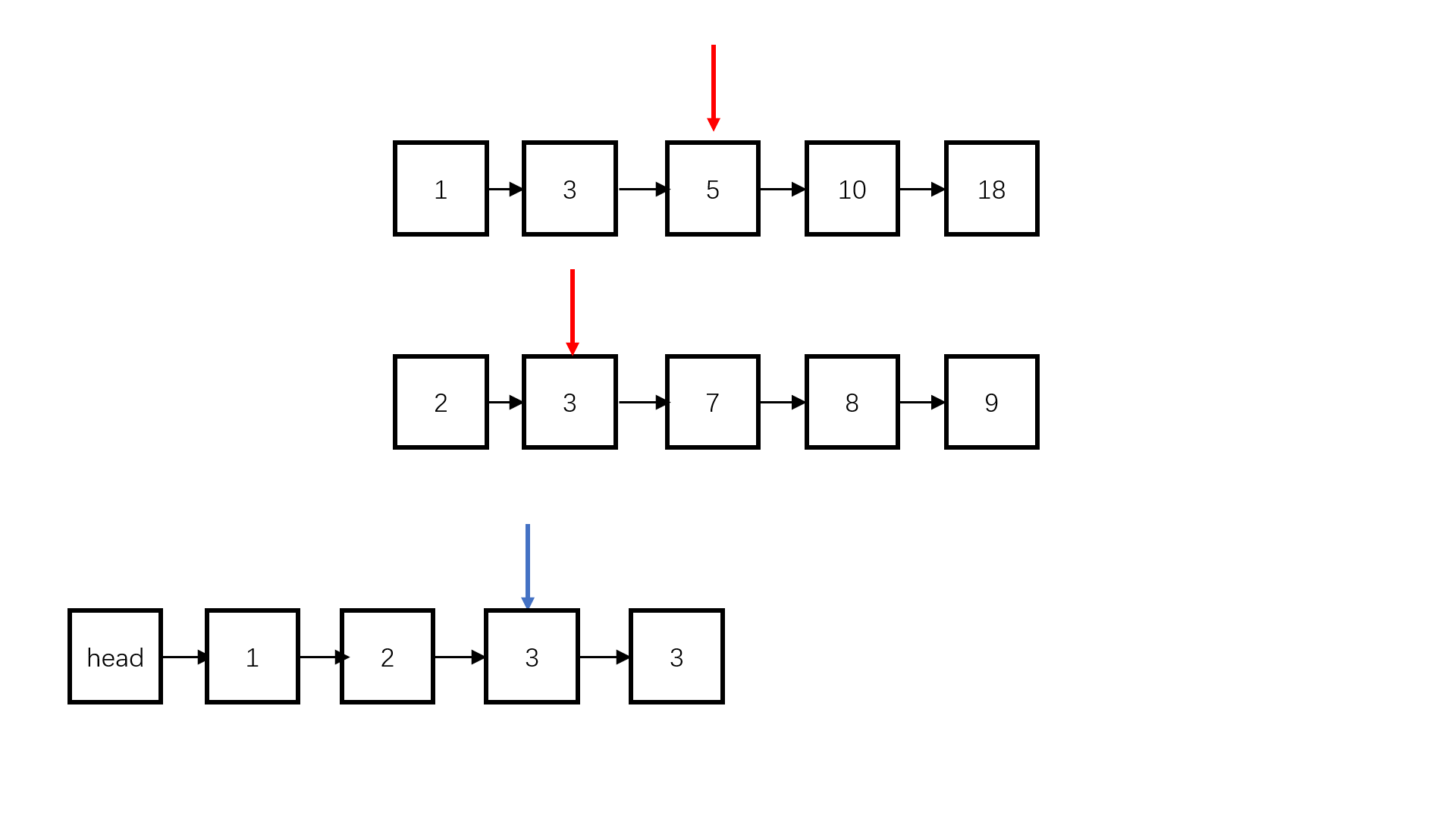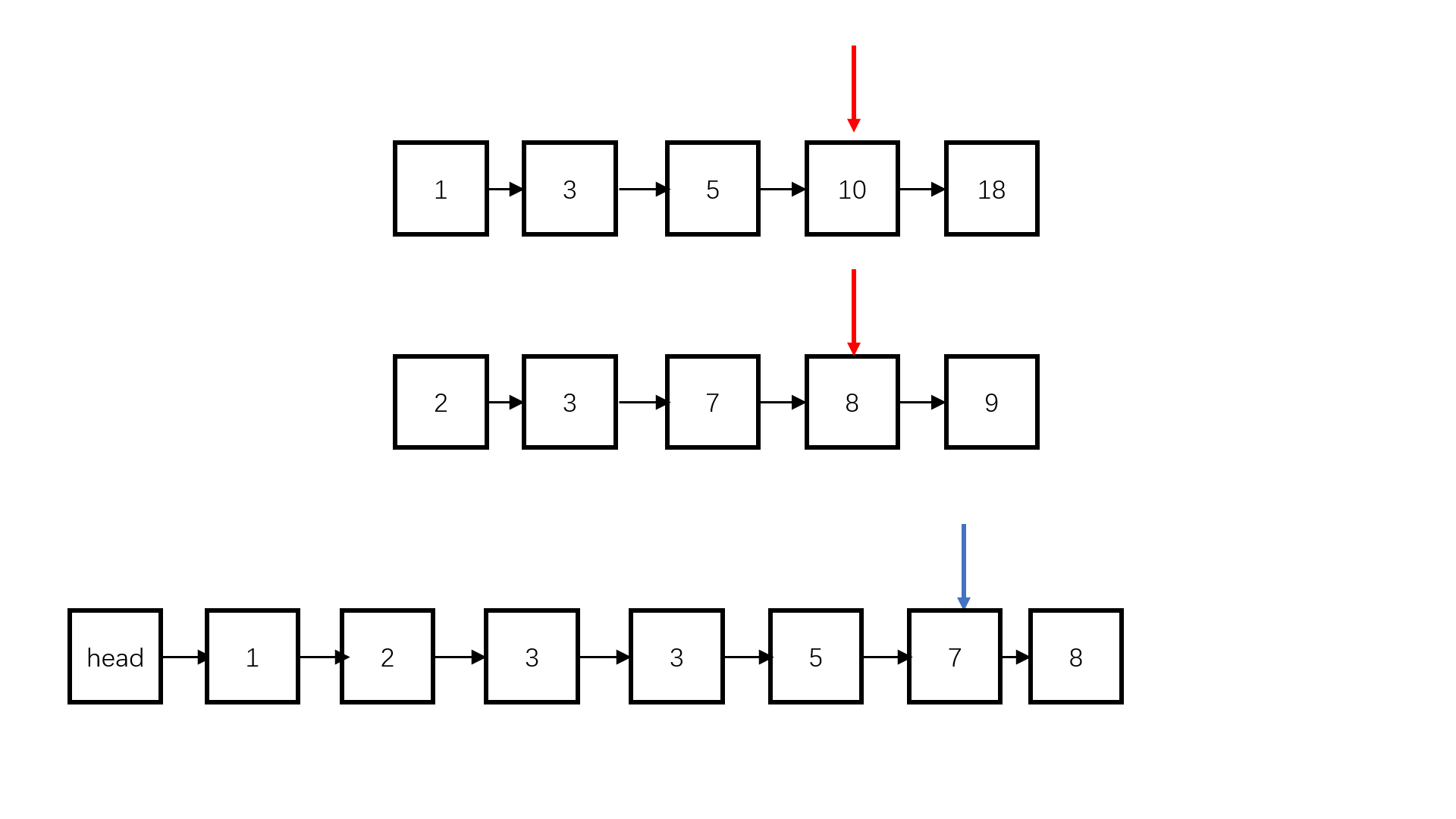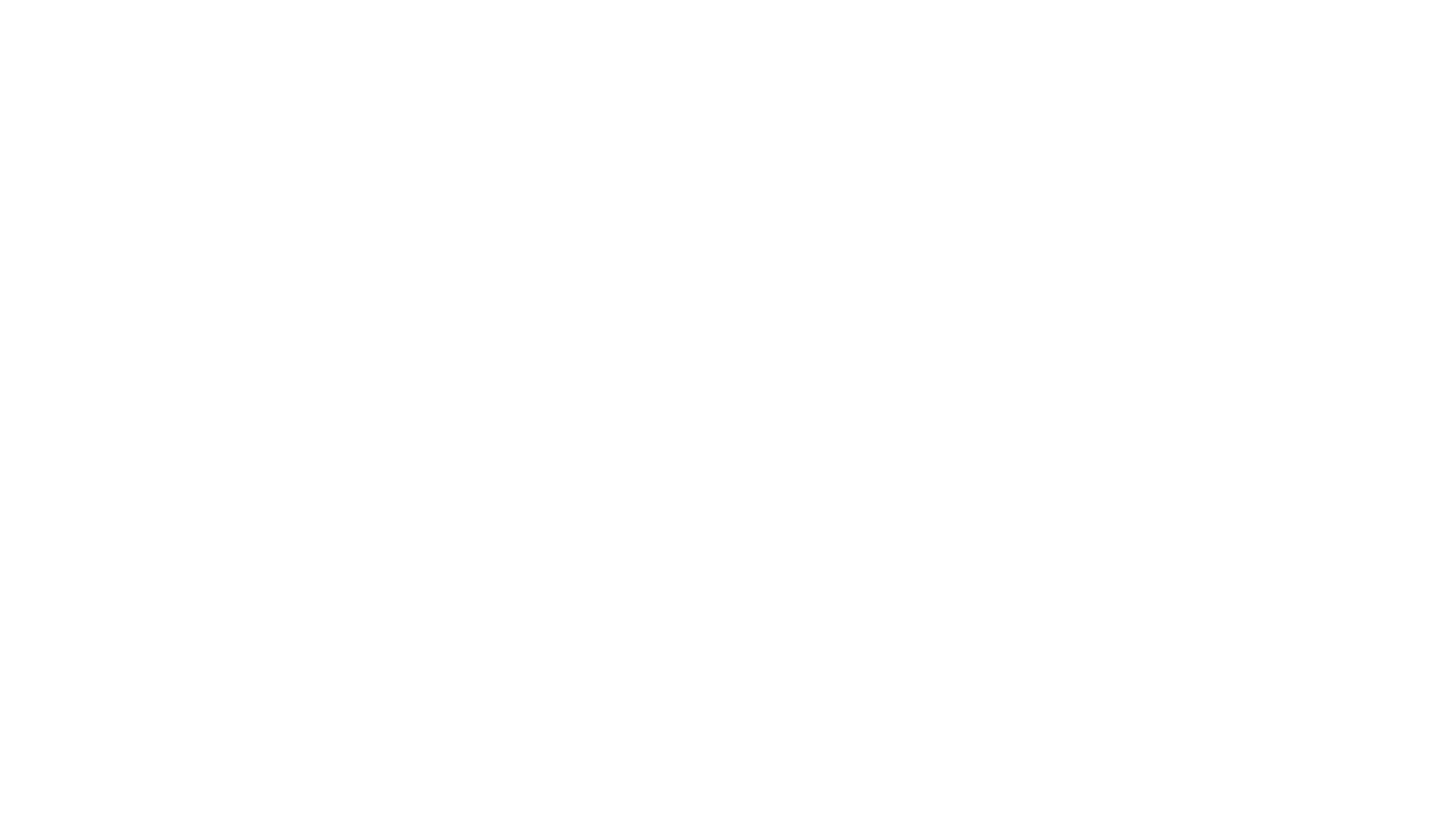
合并两个有序链表

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
    // 一条链表为空，必然返回另一条链表，即使另一条链表也为空
    if (list1 == null) {
        return list2;
    }
    if (list2 == null) {
        return list1;
    }
    // 新建一个虚拟头节点(新链表)，后面连接两条链表排序后的节点
    ListNode dummy = new ListNode(-1);
    // 三个指针分别指向虚拟头节点，list1，list2
    ListNode p = dummy, p1 = list1, p2 = list2;
    // 当两条链表都不为空的时候遍历
    while (p1 != null && p2 != null) {
        // 小的节点加在新链表后面
        if (p1.val <= p2.val) {
            p.next = p1;
            // 只移动取值的指针
            p1 = p1.next;
            // 新链表指针也要移动
            p = p.next;
        } else {
            p.next = p2;
            // 只移动取值的指针
            p2 = p2.next;
            // 新链表指针也要移动
            p = p.next;
        }
    }
    // 哪条链表有剩余(剩余的值一定比前面都大)，就直接连在新链表后面。
    if (p1 != null) {
        p.next = p1;
    }
    if (p2 != null) {
        p.next = p2;
    }
    // 返回时去掉虚拟头结点
    return dummy.next;
}

Tips

虚拟头节点，即代码中的 dummy 节点。使用虚拟头节点可以避免处理指针 p 为空的情况，降低代码的复杂性。

当我们需要创造一条新链表的时候，可以使用虚拟头节点简化边界情况的处理。比如本题中两条链表要合并成一条新的有序链表，这时需要创造一条新链表就可以使用。再比如要将一条链表分解成两条链表，这时候要创建两条新链表，也可以使用。

时间复杂度

\(O(n)\)

最坏情况下，遍历两个链表一共 2 * N 个节点

空间复杂度

\(O(1)\)

无额外辅助空间，返回的链表是原有节点组装，是必要空间。

⭐️分隔链表(力扣86)

题目描述

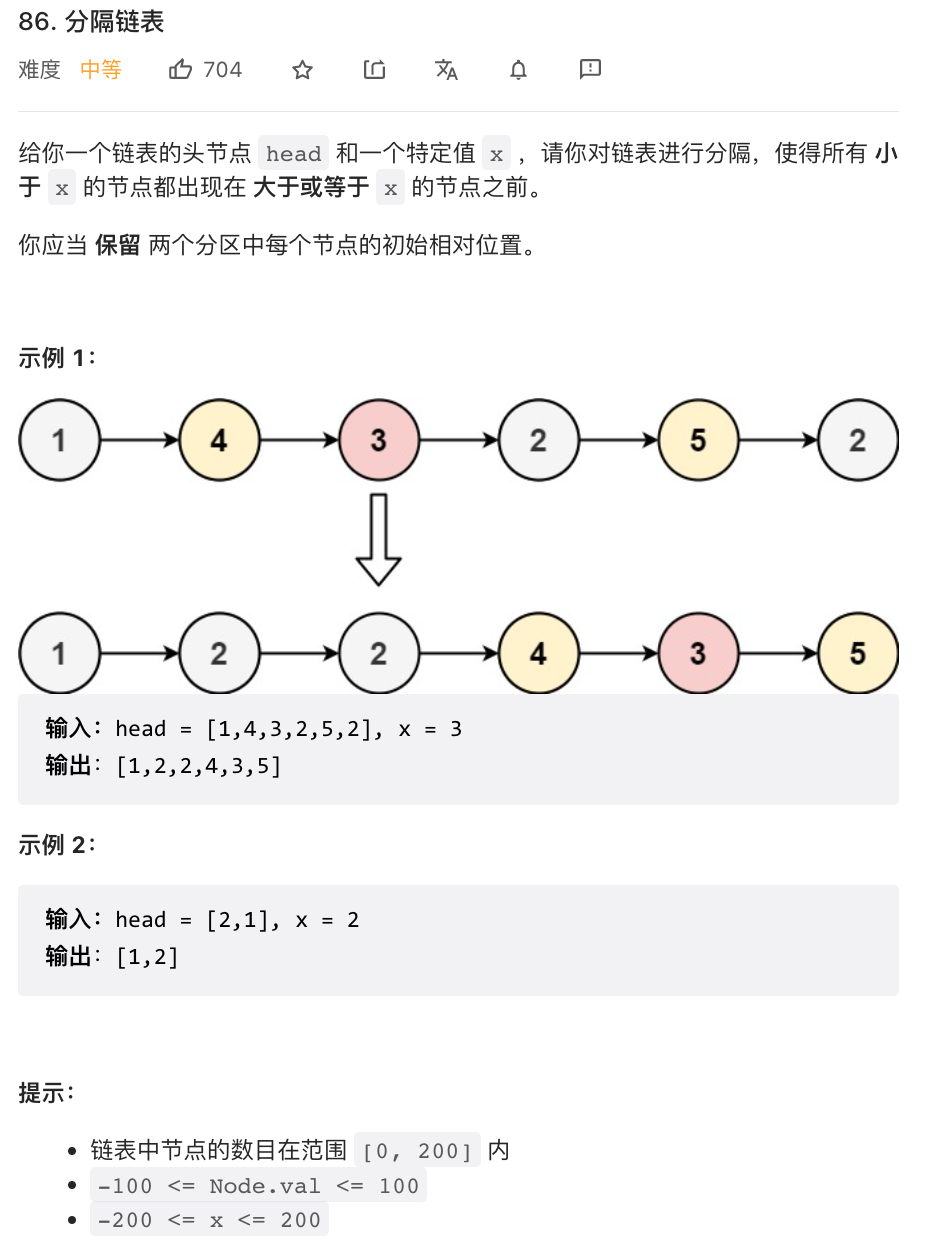
力扣-86-分隔链表

思路(双指针)

在上一题中，合并两个有序链表，是将两个有序链表合二为一。而本题是将原链表一分为二，然后再合并成一条链表。具体来说，就是将原链表分成两条小链表，一条链表的元素都小于 x，另一条链表中的元素都大于等于 x，最后将两条链表再拼接到一起就可以了。两条小链表的构建过程就需要用到「双指针」技巧。

分割链表

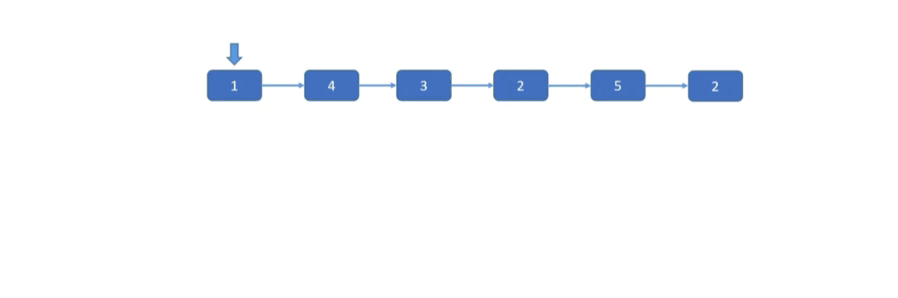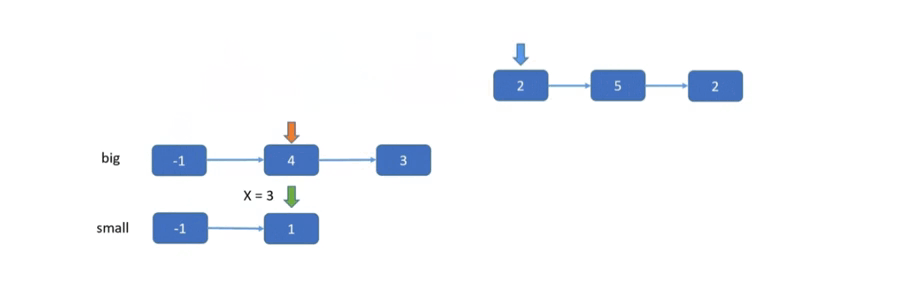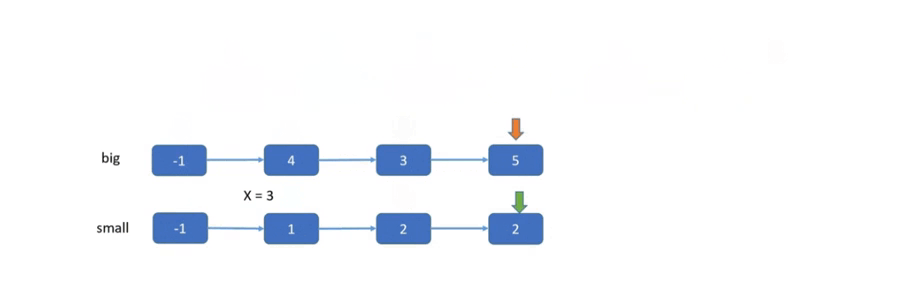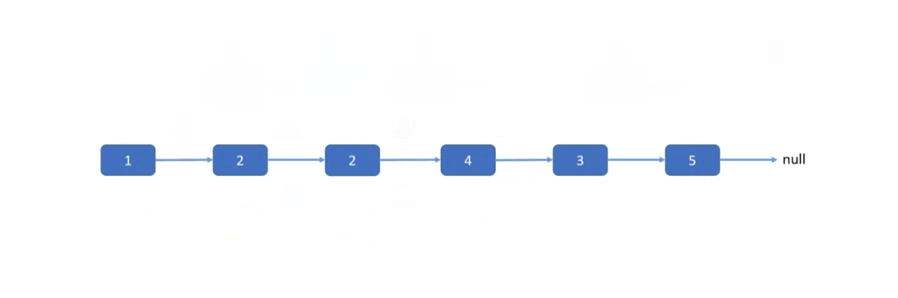
参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public ListNode partition(ListNode head, int x) {
    if (head == null) {
        return head;
    }
    // 存放小于 x 的链表的虚拟头节点
    ListNode dummyLess = new ListNode(-1);
    // 存放大于等于 x 的链表的虚拟头节点
    ListNode dummyMore = new ListNode(-2);
    // p 指针负责遍历原链表，pLess 负责生成小于 x 的结果链表，pMore 负责生成大于等于 x 的结果链表
    ListNode p = head, pLess = dummyLess, pMore = dummyMore;
    while (p != null) { // 原链表不为空
        if (p.val < x) {
            pLess.next = p;
            pLess = pLess.next;    
        } else {
            pMore.next = p;
            pMore = pMore.next;
        }
        // !!! 如果不断开，会成环报错，新手务必注意！
        // 断开原链表中的每个节点的 next 指针
        ListNode nxt = p.next; // 记录原链表中当前节点的下个节点
        p.next = null; // 当前节点的 next 指针设为空
        p = nxt;
    }
    // 小 x 链表连接大 x 链表
    pLess.next = dummyMore.next;
    // 返回时去掉虚拟头结点
    return dummyLess.next;
}

Tips

在循环代码块中，必须断开原链表中每个节点的 next 指针，即将原链表节点的 next 指针设为 null，然后才能向后移动指针，否则就会连接成环从而导致答案错误。

时间复杂度

\(O(n)\)

最坏情况下，需要完整遍历一遍原链表。

空间复杂度

\(O(1)\)

使用了常数个指针，没有额外辅助空间。

合并 K 个升序链表(力扣23)

题目描述

力扣-23-合并 K 个升序链表

思路(k个指针)

我们可以准备 k 个指针，分别放在 k 个链表头，每次取出最小的元素，加入到新的大链表中，指针后移，继续比较，每次出去的都是最小元素，就完成了题目的要求。

在 Java 中，我们可以借助优先级队列 PriorityQueue 来实现。优先级队列本质上是一种堆排序容器，根据传入的比较器确定是大根堆还是小根堆，默认是小根堆。小根堆的堆顶是容器中最小的元素，其余更大的元素在堆下方。想要了解这种结构，可以访问Data Structure Visualizations网站去查看小根堆的排序过程。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public ListNode mergeKLists(ListNode[] lists) {
    // 判空
    if (lists == null || lists.length == 0) {
        return null;
    }
    // 优先级队列，小根堆
    PriorityQueue<ListNode> pq = new PriorityQueue<>((a, b) -> a.val - b.val);
    // 将 k 个链表的头节点加入小根堆
    for (ListNode head : lists) {
        // 头节点不为空才能加入
        if (head != null)
            pq.add(head);
    }
    // 要新建一个结果链表，所以新建一个虚拟头节点，指针 p 用于构建结果链表
    ListNode dummy = new ListNode(-1), p = dummy;
    while (!pq.isEmpty()) {
        // 取出最小元素的节点
        ListNode cur = pq.poll();
        // 连接到结果链表上
        p.next = cur;
        p = p.next;
        // 如果被取出的节点后续有节点，加入到小根堆中
        if (cur.next != null) {
            pq.add(cur.next);
        }
    }
    // 返回时去掉虚拟头节点
    return dummy.next;
}

时间复杂度

\(O(nlog_2k)\)

n 为所有链表总节点数，最坏要遍历所有节点，每次加入优先级队列排序需要 \(O(log_2k)\)。

空间复杂度

\(O(k)\)

优先队列的大小不会超过 k。

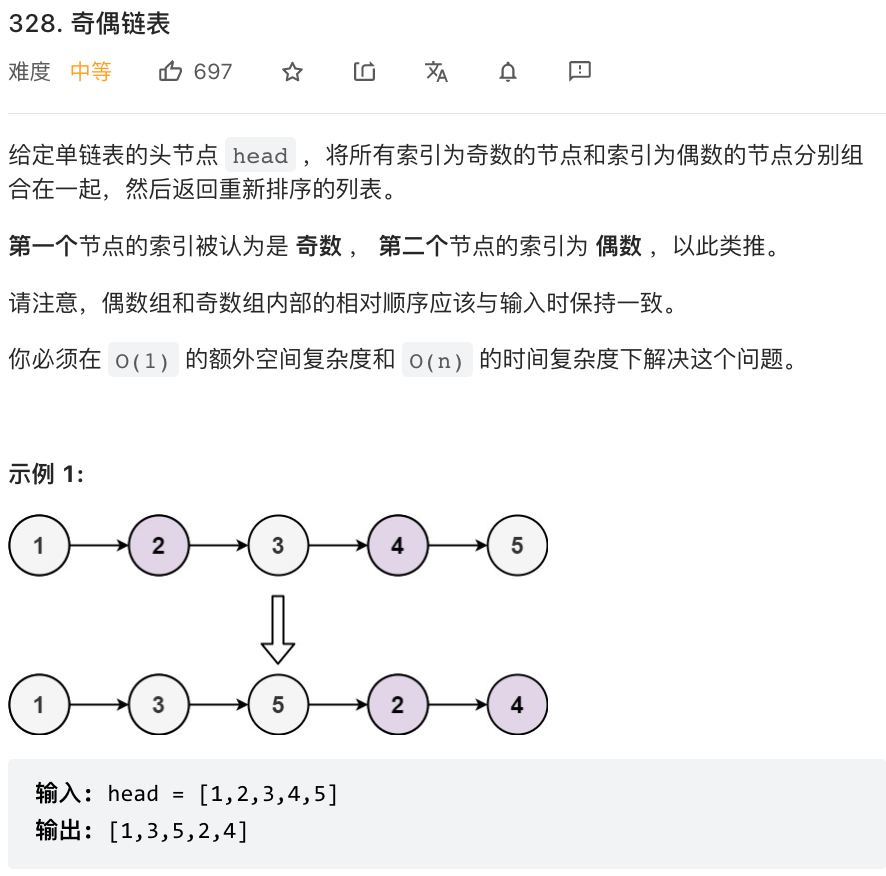
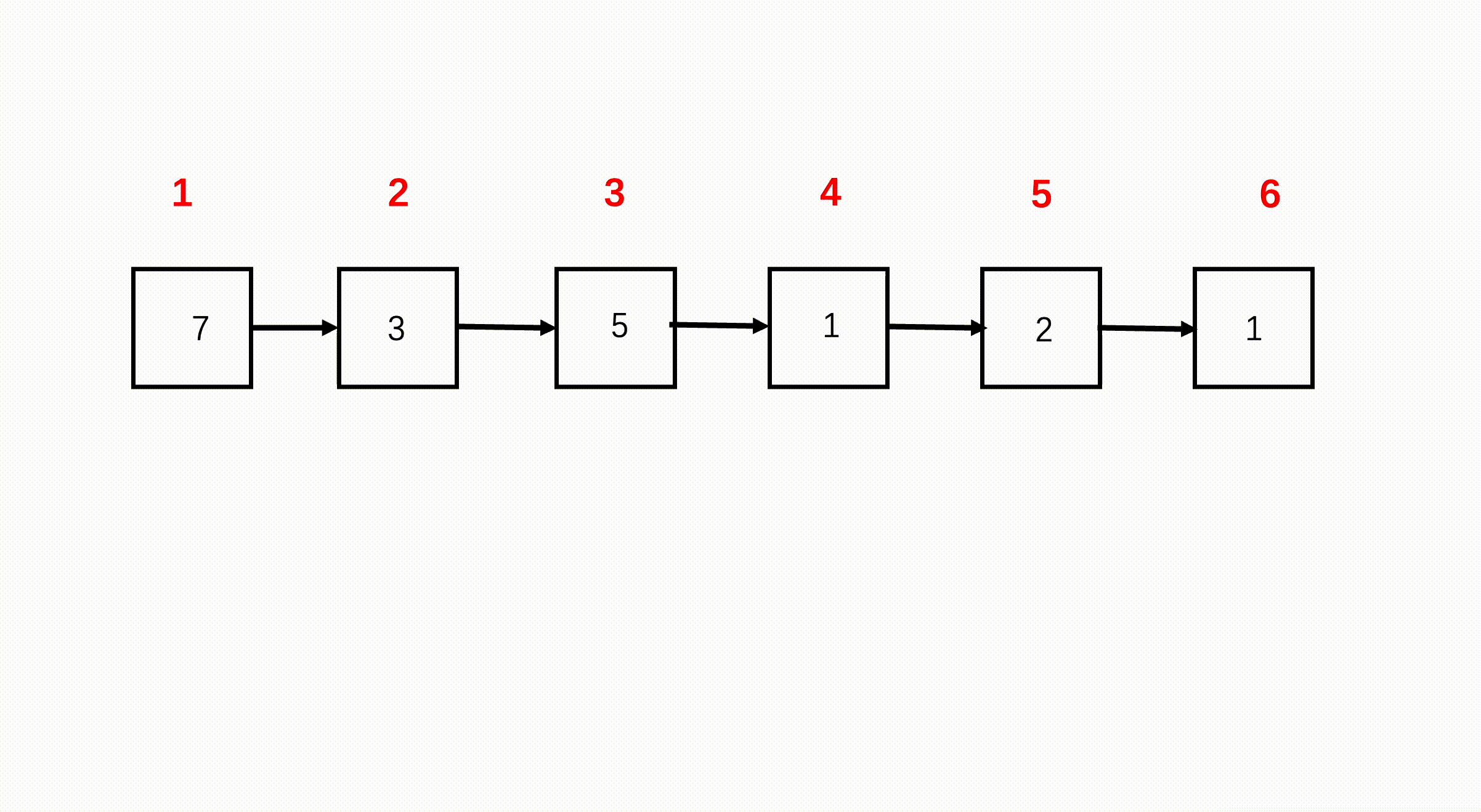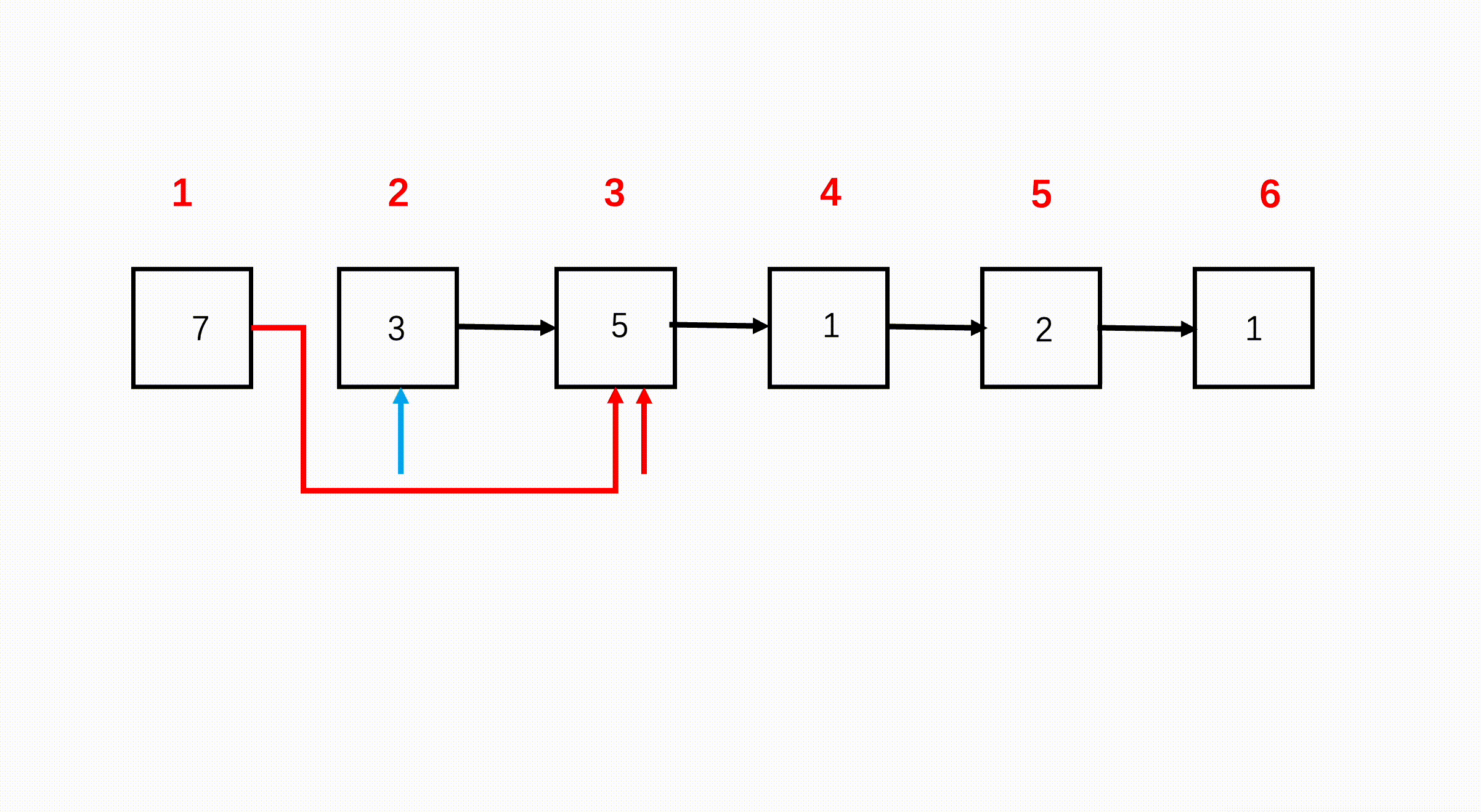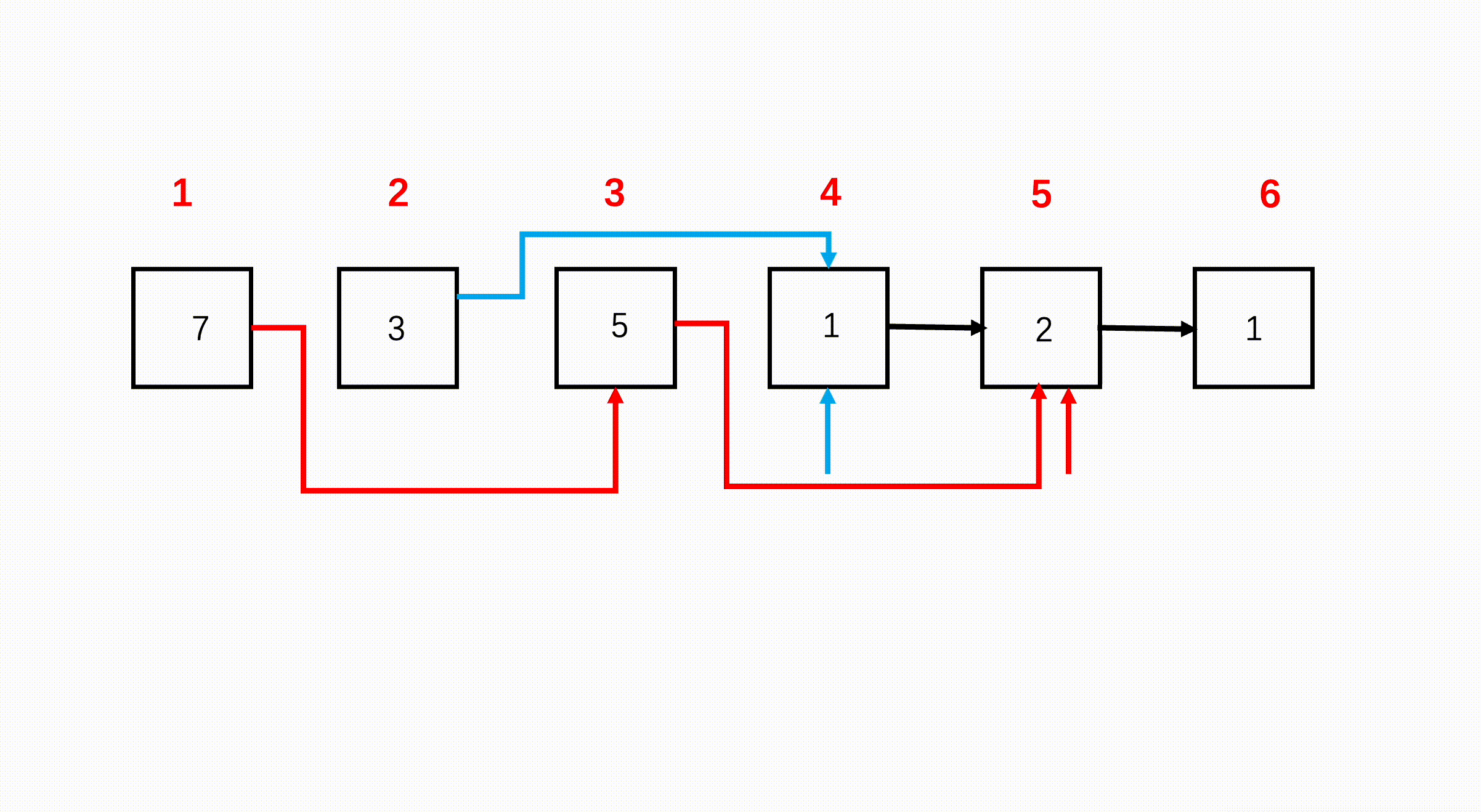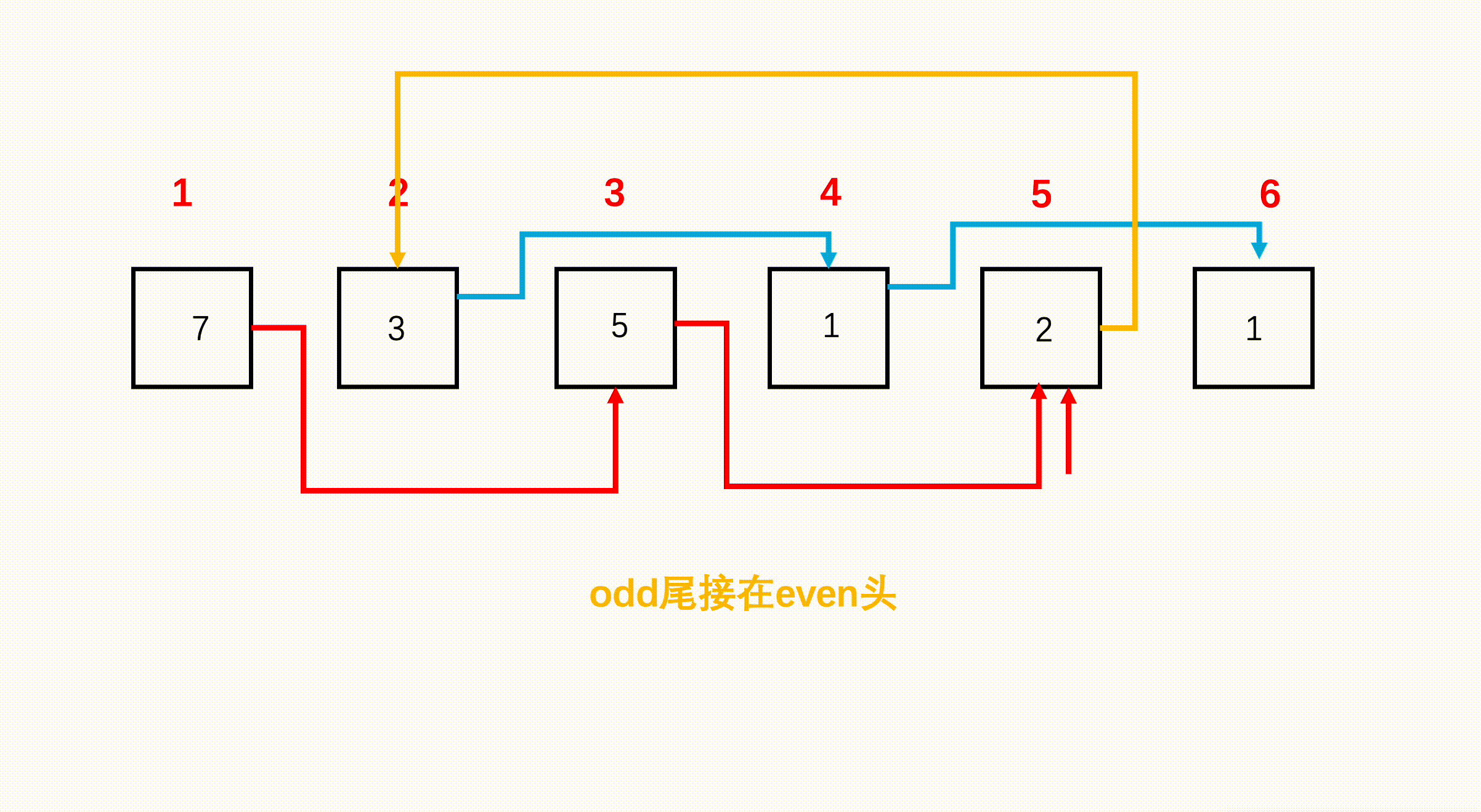
⭐️奇偶链表(力扣328)

题目描述

奇偶链表(力扣328)

思路(双指针)

这道题直接使用两个指针同方向遍历链表，第一个节点索引为奇数，第二个节点索引为偶数，第三个节点索引为奇数。我们可以直接断掉节点 1 和节点 2 之间的连接，让节点 1 的 next 指向节点 3，偶数索引节点也是如此。

双指针同向遍历

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public ListNode oddEvenList(ListNode head) {
    // 如果链表为空，不用重排
    if(head == null) {
        return head;
    }
    // 奇数索引节点指针
    ListNode odd = head;
    // 偶数索引节点指针，可能为空
    ListNode even = head.next;
    // 标记偶数索引头节点，用于奇偶索引链表连接
    ListNode evenHead = even;
    while (even != null && even.next != null) {
        // 奇数索引节点的 next 连向偶数索引节点的下一个
        odd.next = even.next;
        // 奇数索引指针后移
        odd = odd.next;
        // 偶数索引节点的 next 连向奇数索引节点的下一个
        even.next = odd.next;
        // 偶数索引指针后移
        even = even.next;
    }
    // 偶数索引链表连在奇数索引链表后面
    odd.next = evenHead;
    return head;
}

时间复杂度

\(O(n)\)

遍历一次链表所有节点。

空间复杂度

\(O(1)\)

常数级指针变量，没有额外辅助空间。

快慢指针类问题

⭐️删除链表的倒数第 N 个结点(力扣19)

题目描述

力扣-19-删除链表的倒数第 N 个结点

思路(双指针)

我们直接讲进阶的实现方式，也就是使用双指针技巧，一趟扫描实现这道题目。

这道题目要用到「双指针」技巧的「快慢指针」，假设 n = 3，我们可以先让快指针走 3 步，然后慢指针此时从链表头结点出发，快慢指针同步前进，当快指针走到 null 时，慢指针正好指向要删除的节点。

由于要删除这个节点，我们还需准备一个虚拟头节点，以及一个指向虚拟头节点的指针(前置指针)，前置指针与慢指针同时同步前进，当慢指针指向要删除节点的时候，前置指针正好指向要删除节点的前一个，然后将前置指针的 next 指针指向要删除节点的下一个节点即可。

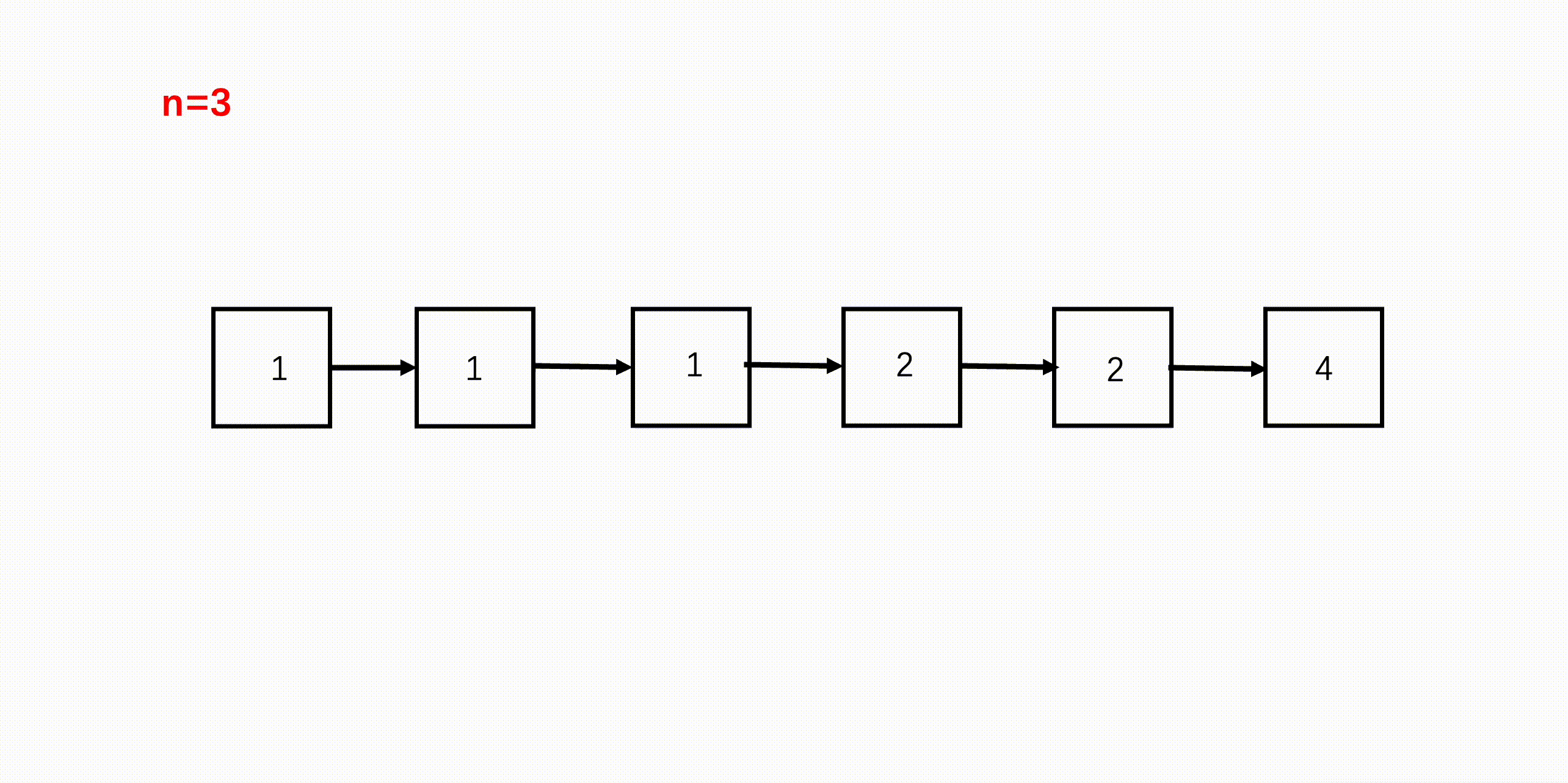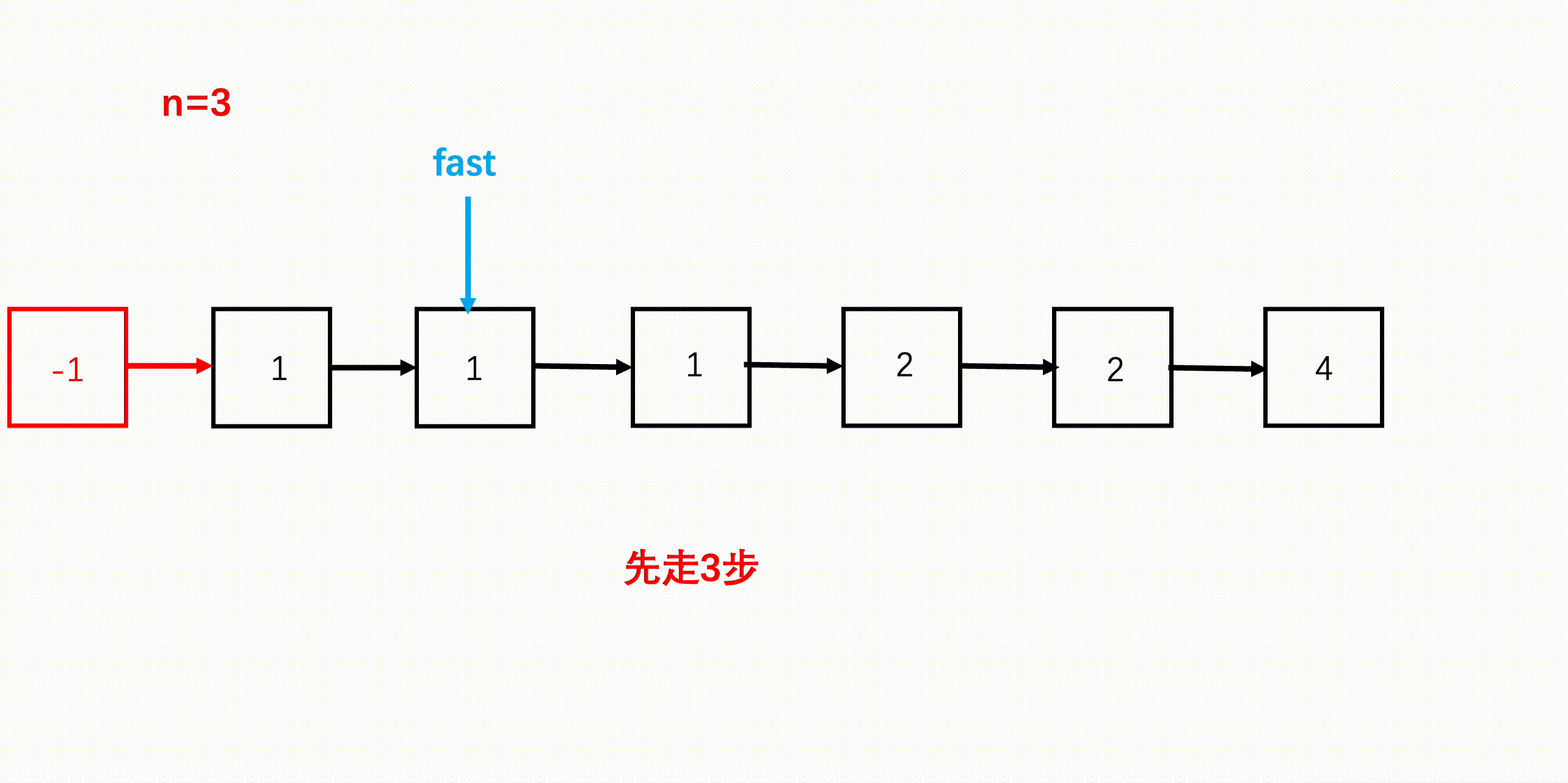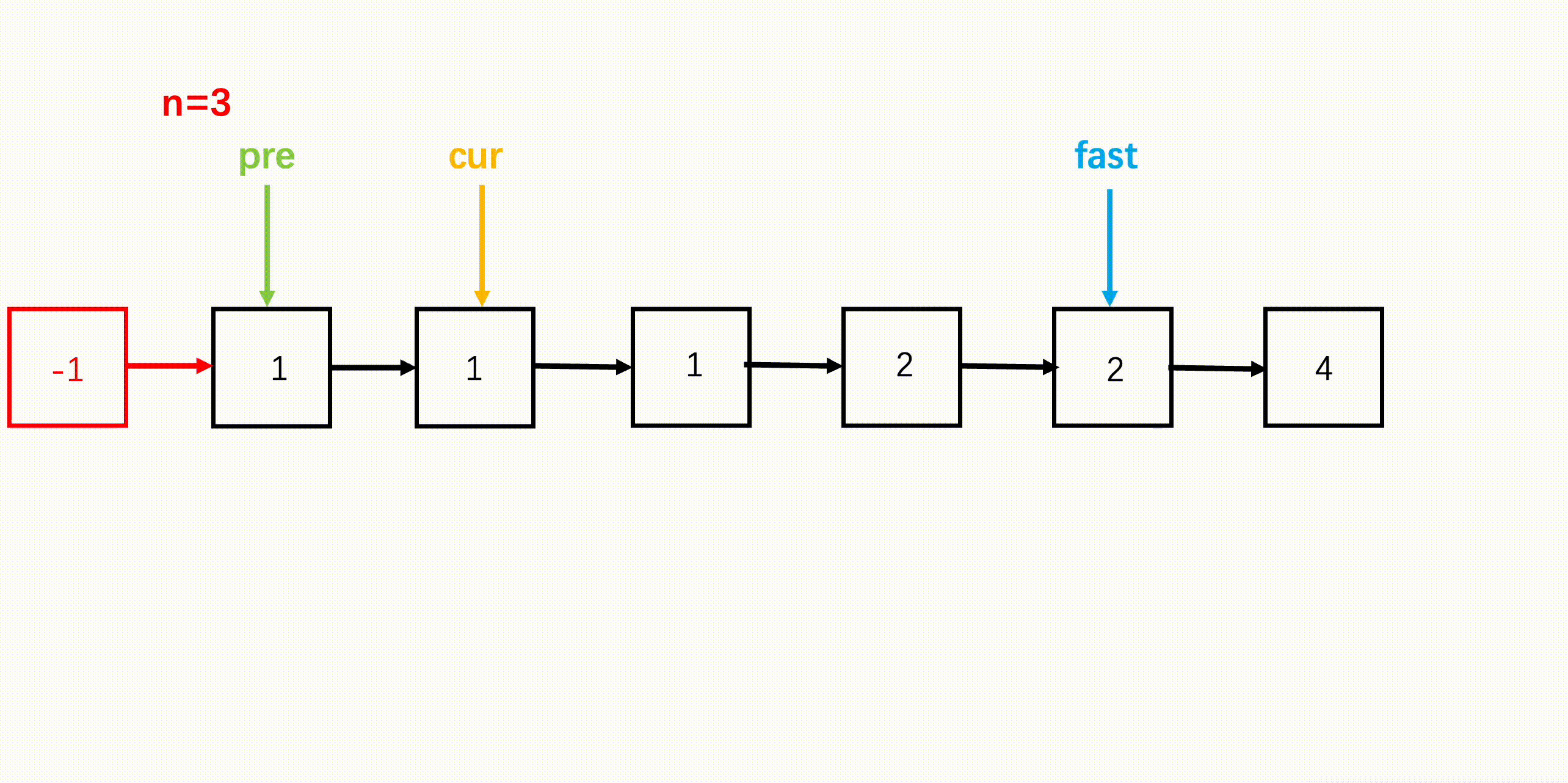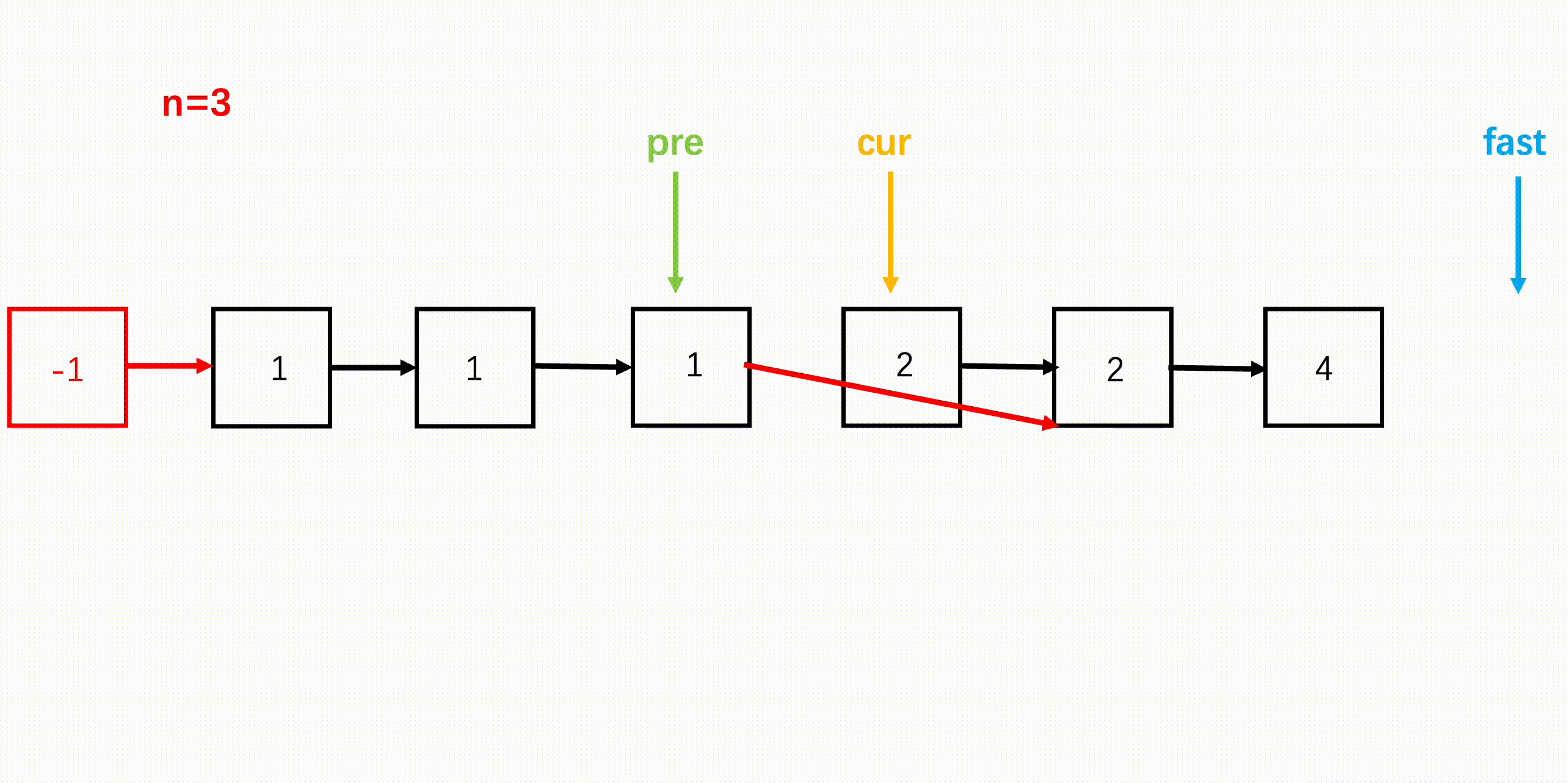
力扣-19-删除链表的倒数第 N 个结点

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public ListNode removeNthFromEnd(ListNode head, int n) {
    // 判空
    if (head == null) {
        return head;
    } 
    // 快指针先走 n 步
    ListNode fast = head;
    for (int i = 0; i < n; i++) {
        fast = fast.next;
    }
    // 给原链表添加一个虚拟头节点
    ListNode dummy = new ListNode(-1);
    dummy.next = head;
    // 准备前置指针和慢指针
    ListNode pre = dummy;
    ListNode slow = head;
    // 前置、快慢指针同步前进，当快指针为空时，慢指针就到了倒数第 n 个位置
    while (fast != null) {
        fast = fast.next;
        slow = slow.next;
        pre = pre.next;
    }
    // 删除慢指针处的节点(倒数第 n 个节点)
    pre.next = slow.next; // help GC
    // 返回时去掉表头
    return dummy.next;
}

时间复杂度

\(O(n)\)

最坏情况下，遍历 n 个链表节点。

空间复杂度

\(O(1)\)

常数级指针变量，无额外辅助空间使用

⭐️链表的中间结点(力扣876)

题目描述

力扣-876-链表的中间结点

思路(双指针)

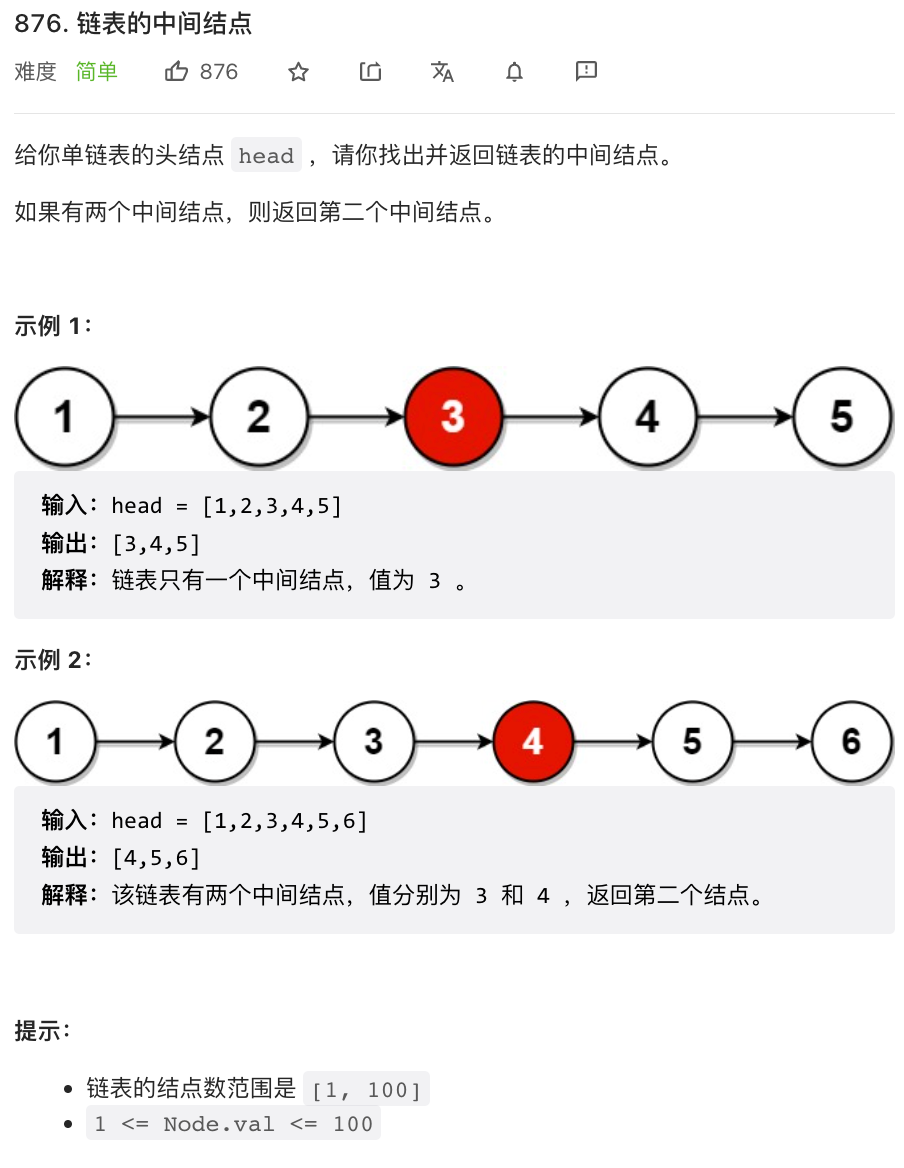
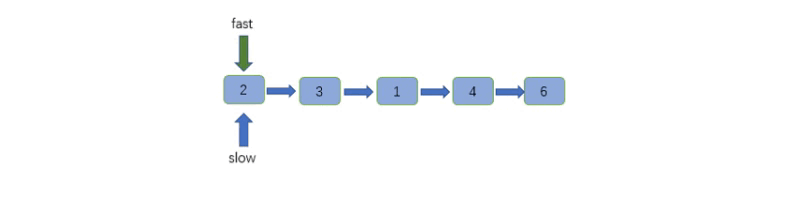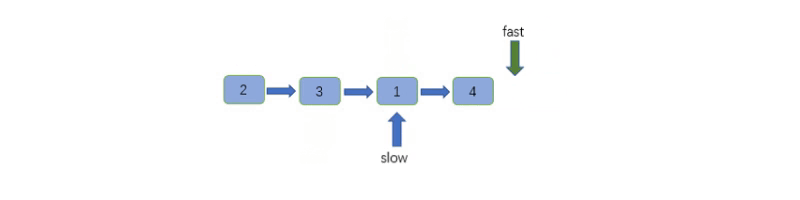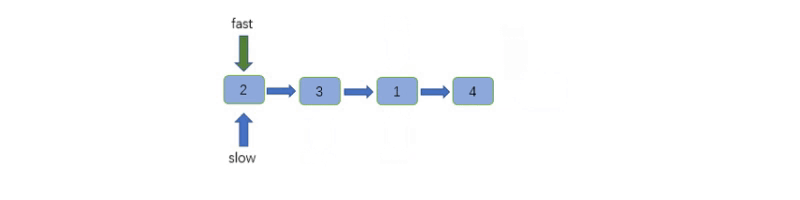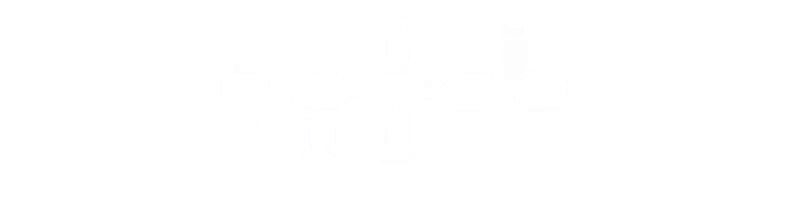
这道题用到了「双指针」技巧的 「快慢指针」技巧，我们快慢指针分别指向链表头节点 head。

快指针每次走两步，慢指针每次走一步，当快指针走到链表末尾时，慢指针正好指向链表的中点。

链表的中间节点

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public ListNode middleNode(ListNode head) {
    if (head == null) {
        return head;
    }
    // 快慢指针分别指向链表头节点 head
    ListNode slow = head, fast = head;
    // 快指针走到链表末尾时停止
    while (fast != null && fast.next != null) {
        // 快指针一次走两步，慢指针一次走一步
        fast = fast.next.next;
        slow = slow.next;
    }
    // 慢指针指向链表中点
    return slow;
}

时间复杂度

\(O(n)\)

空间复杂度

\(O(1)\)

常数级指针变量，无额外辅助空间使用。

左右指针类问题

⭐️回文链表(力扣234)

题目描述

回文链表(力扣234)

思路(双指针)

这道题我们直接讲最优方案，也就是时间复杂度为 \(O(n)\)，空间复杂度为 \(O(1)\) 的解题思路。

我们首先使用 「快慢指针寻中法」 找到链表的中点。

双指针寻中法

然后反转后半部分的链表，然后重定向「快慢指针」使用 「左右指针技巧」 依次比对链表节点值是否相等。

反转链表并重定向快慢指针

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public boolean isPalindrome(ListNode head) {
    // 空链表为回文链表
    if (head == null) {
        return true;
    }
    // 快慢指针寻中法
    ListNode fast = head, slow = head;
    while (fast != null && fast.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    // 中点处反转
    slow = reverseList(slow); // slow 现在指向右半部分的第一个节点
    fast = head; // fast 现在指向左半部分的第一个节点
    while (slow != null) {
        // 比较判断节点值是否相等
        if (slow.val != fast.val) {
            return false;
        }
        fast = fast.next;
        slow = slow.next;
    }
    return true;
}

public ListNode reverseList(ListNode head) {
    ListNode pre = null, cur = head, succ = null;
    while (cur != null) {
        succ = cur.next;
        cur.next = pre;
        pre = cur;
        cur = succ;
    }
    return pre;
}

时间复杂度

\(O(n)\)

双指针找到中点遍历半个链表，后续反转链表为\(O(n)\)，然后再遍历两份半个链表。

空间复杂度

\(O(1)\)

常数级变量，无额外辅助空间使用。

环形链表类问题

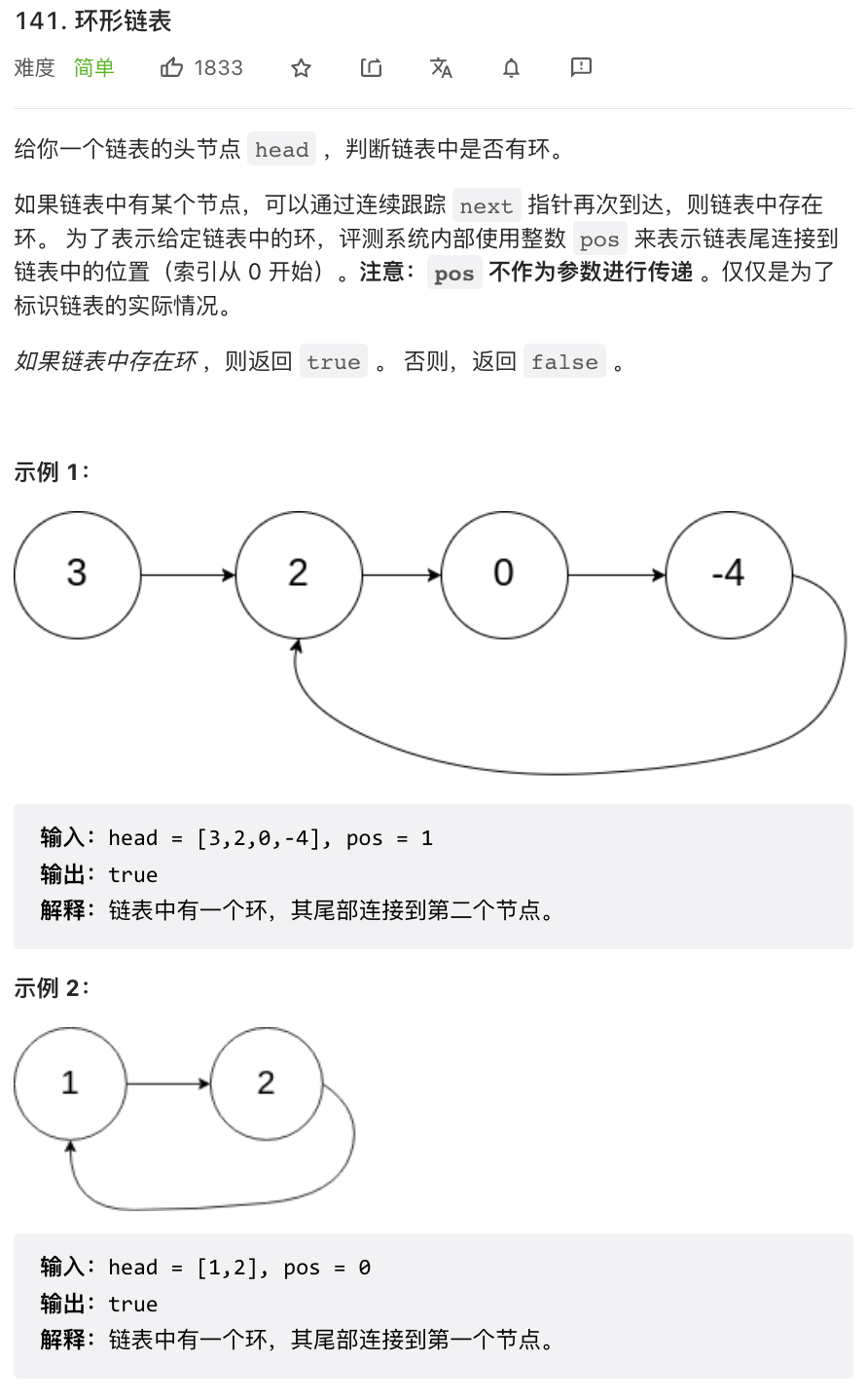
⭐️环形链表(力扣141)

题目描述

环形链表(力扣141)

思路(双指针)

这道题用到的也是「快慢指针」技巧。环形链表的环一定在链表末尾，并且末尾没有 null 了。根据这个特点，我们使用快慢指针同向访问链表，因为速度不一致，如果有环的话，快慢指针一定会相遇；如果没有环的话，快指针一定会遇到空指针。

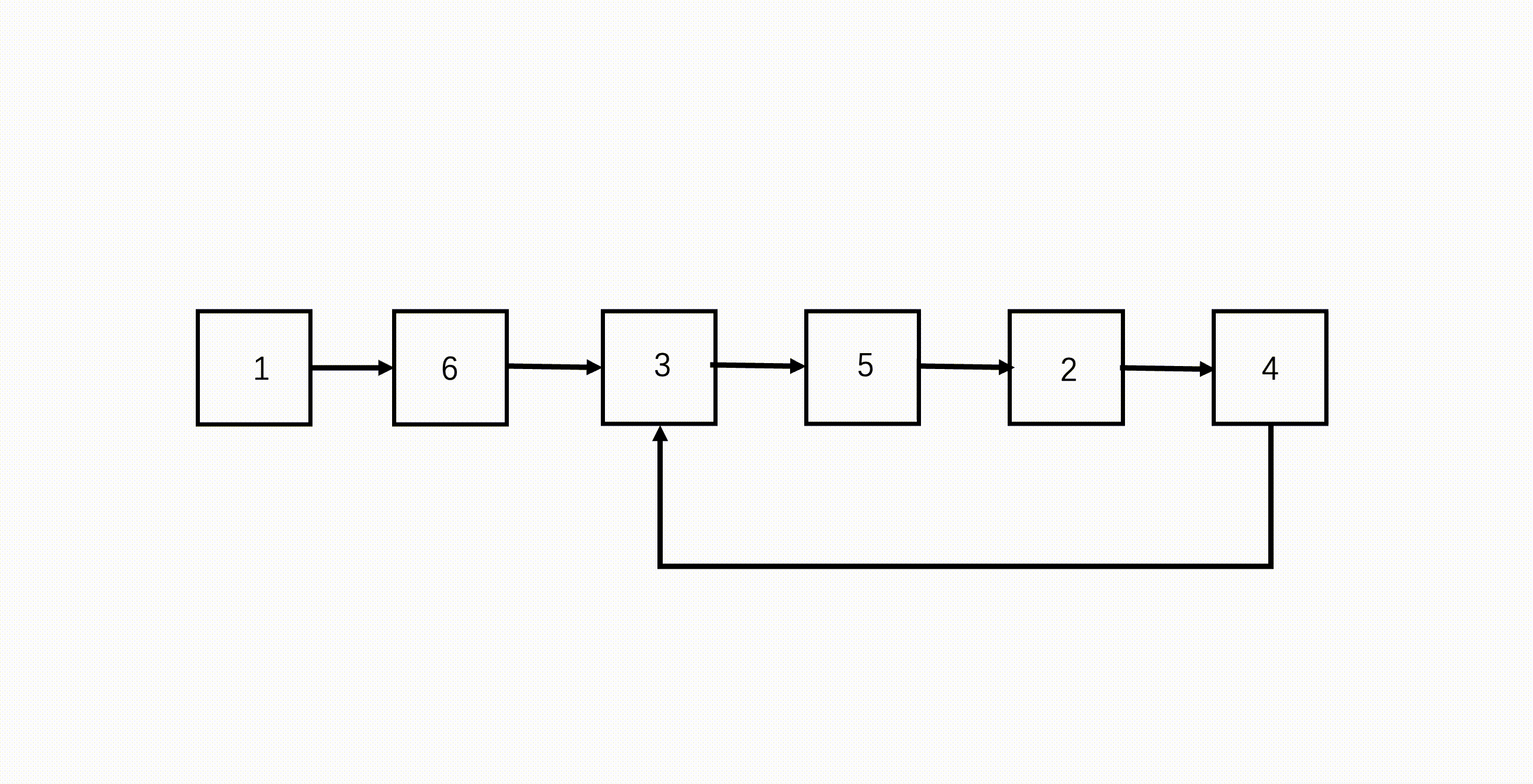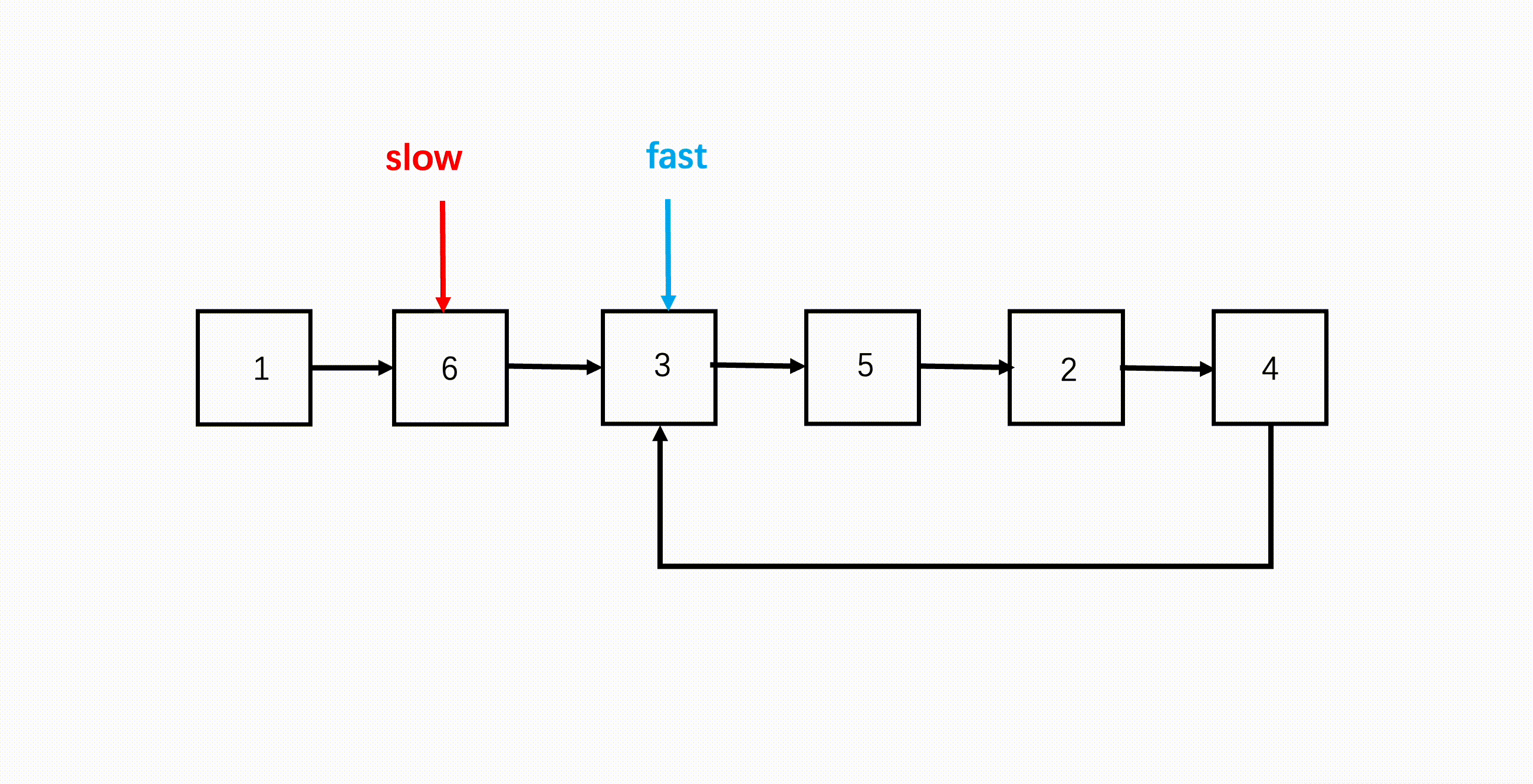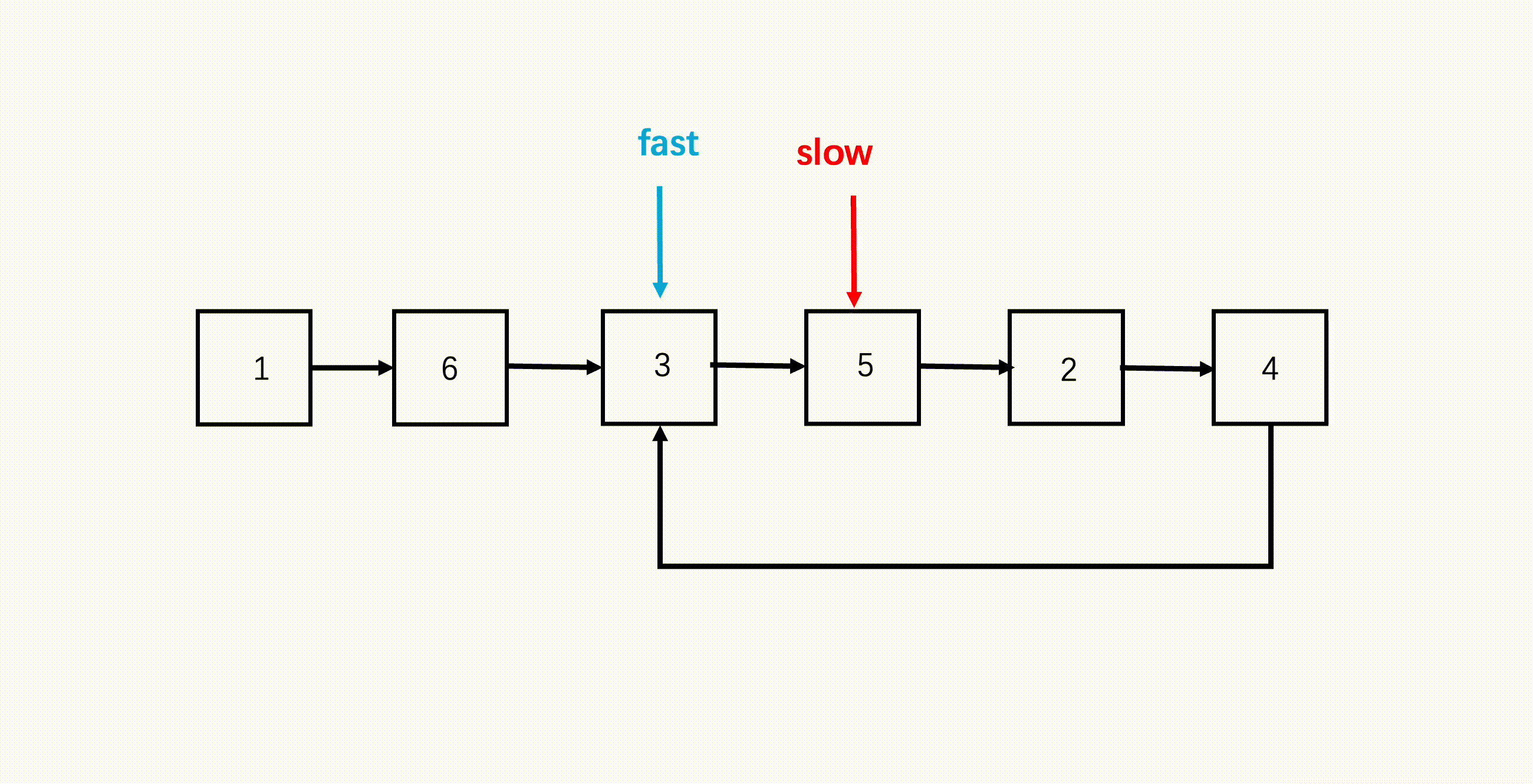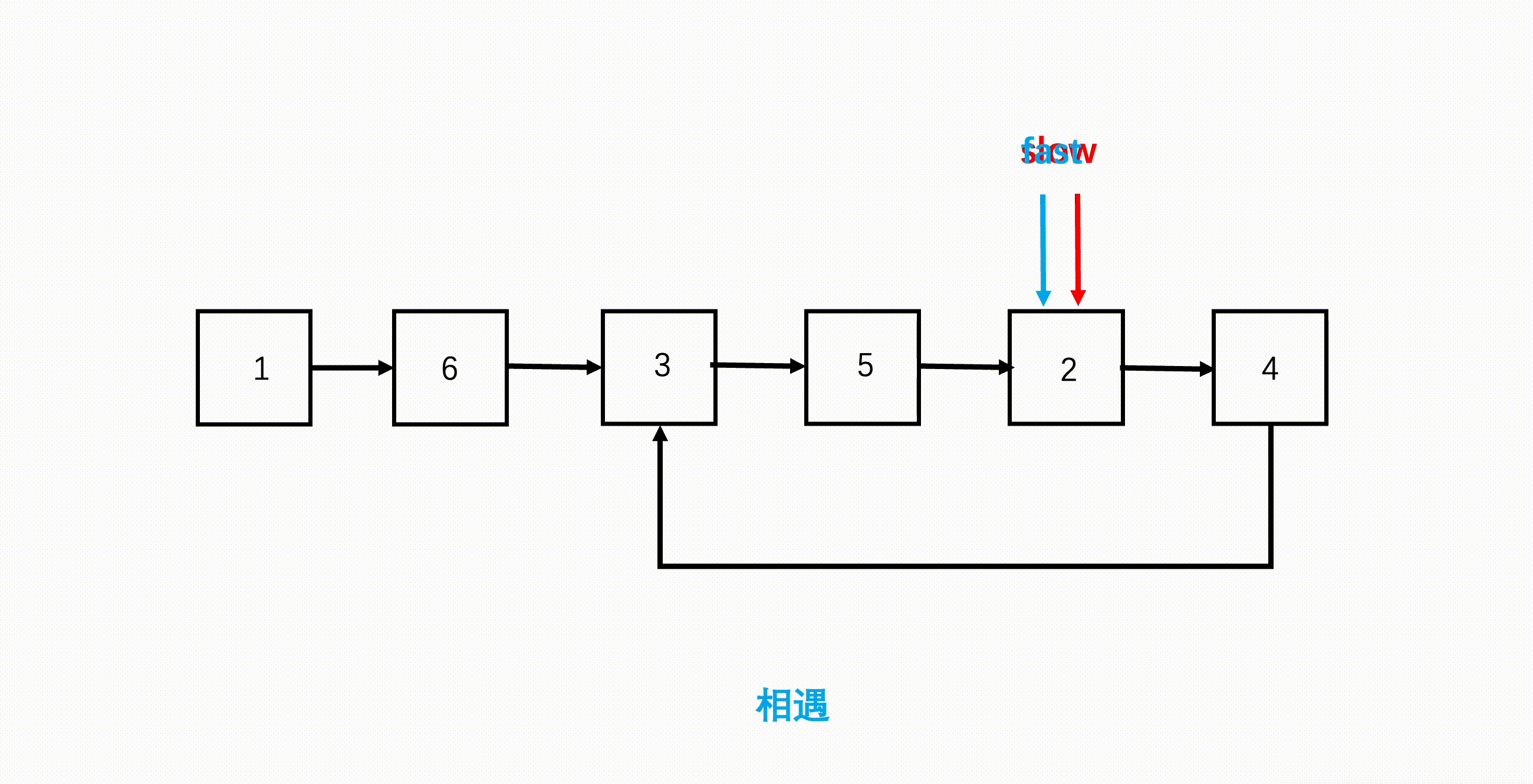
双指针判断链表是否有环

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public boolean hasCycle(ListNode head) {
    // 判空
    if (head == null || head.next == null) {
        return false;
    }
    // 快慢双指针，初始指向链表头 head
    ListNode slow = head, fast = head;
    // 快指针走到末尾时停止
    while (fast != null && fast.next != null) {
        // 快慢指针移动
        fast = fast.next.next;
        slow = slow.next;
        // 快慢指针相遇则有环
        if (slow == fast) {
            return true;
        }
    }
    // 快指针走到末尾，则没有环
    return false;
}

时间复杂度

\(O(n)\)

最坏情况下遍历链表 n 个节点。

空间复杂度

\(O(1)\)

仅使用了两个指针，没有额外辅助空间。

⭐️环形链表入口节点(力扣142)

题目描述

环形链表入口节点(力扣142)

思路(双指针)

这道题也是使用「快慢指针」技巧，难点在于如何找到环的入口节点。我会先说如何解决这道题，理论推导过程我也会给出，如果觉得很难懂可以直接跳过，记住解题方法就可以了。

解法就是使用上一题(判断链表是否有环)的方法，找到相遇节点，然后慢指针留在相遇节点，快指针回到链表头节点，之后两个指针同步逐个元素地遍历链表，当两者再次相遇的节点就是环的入口节点。

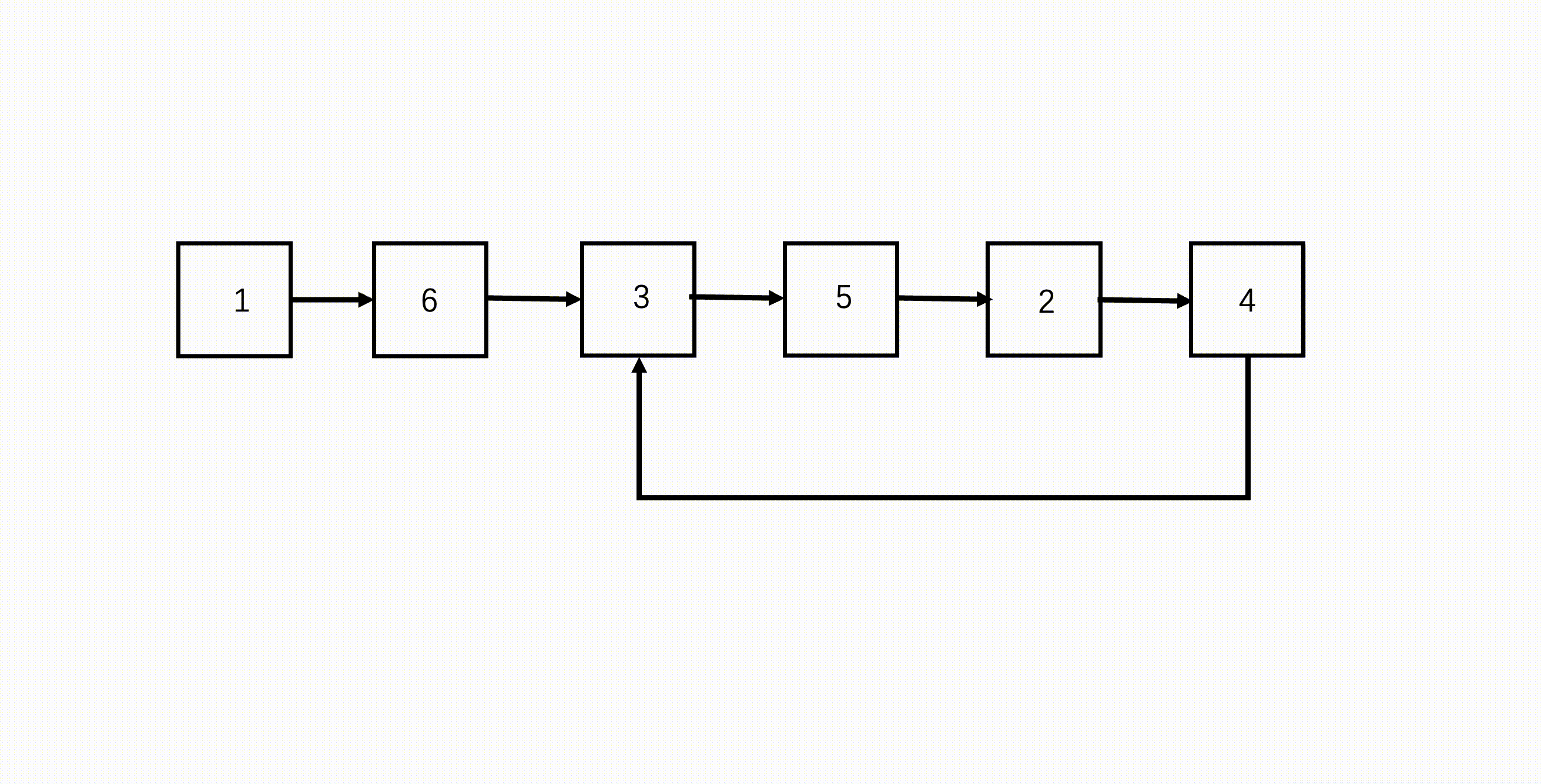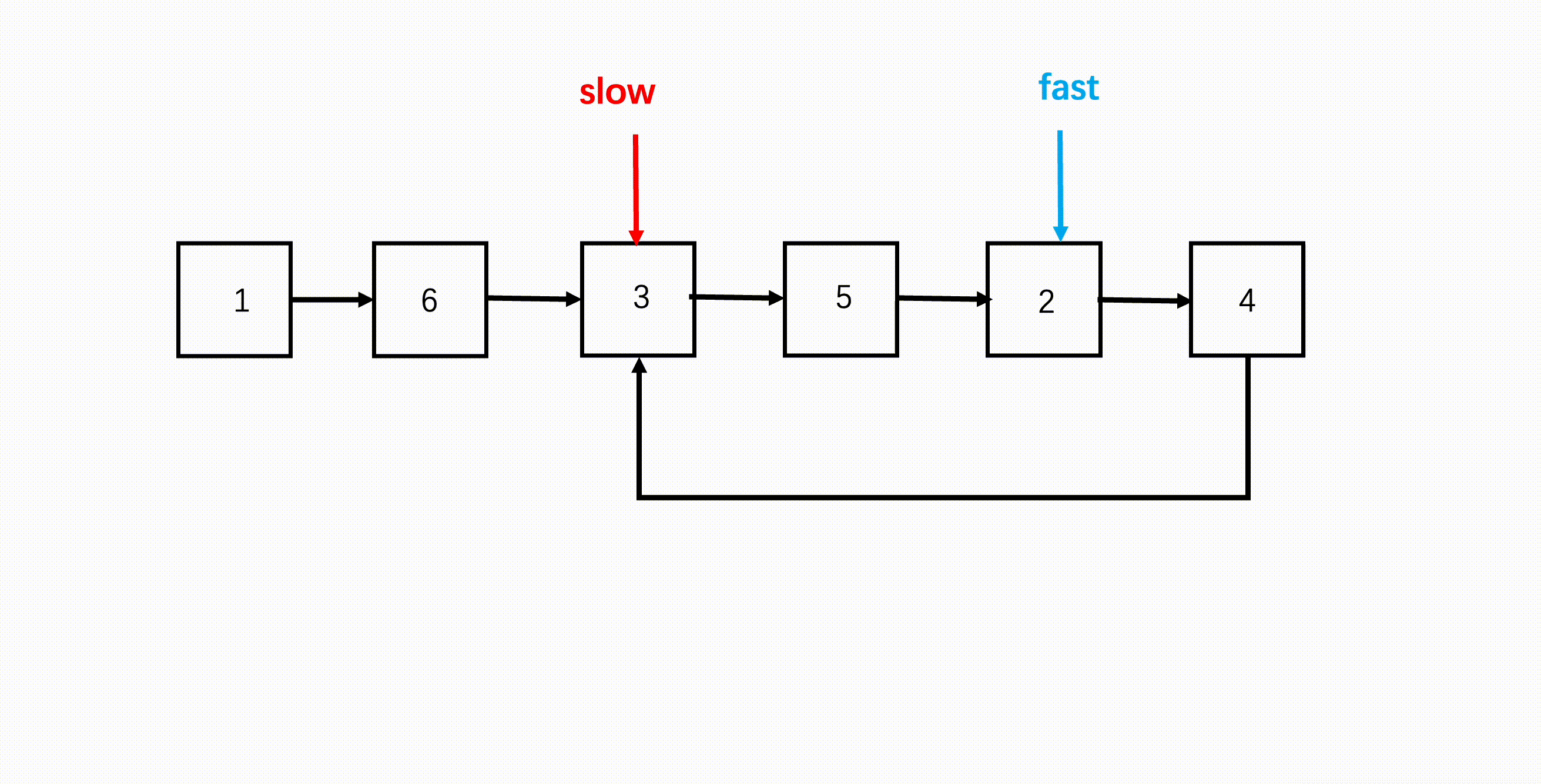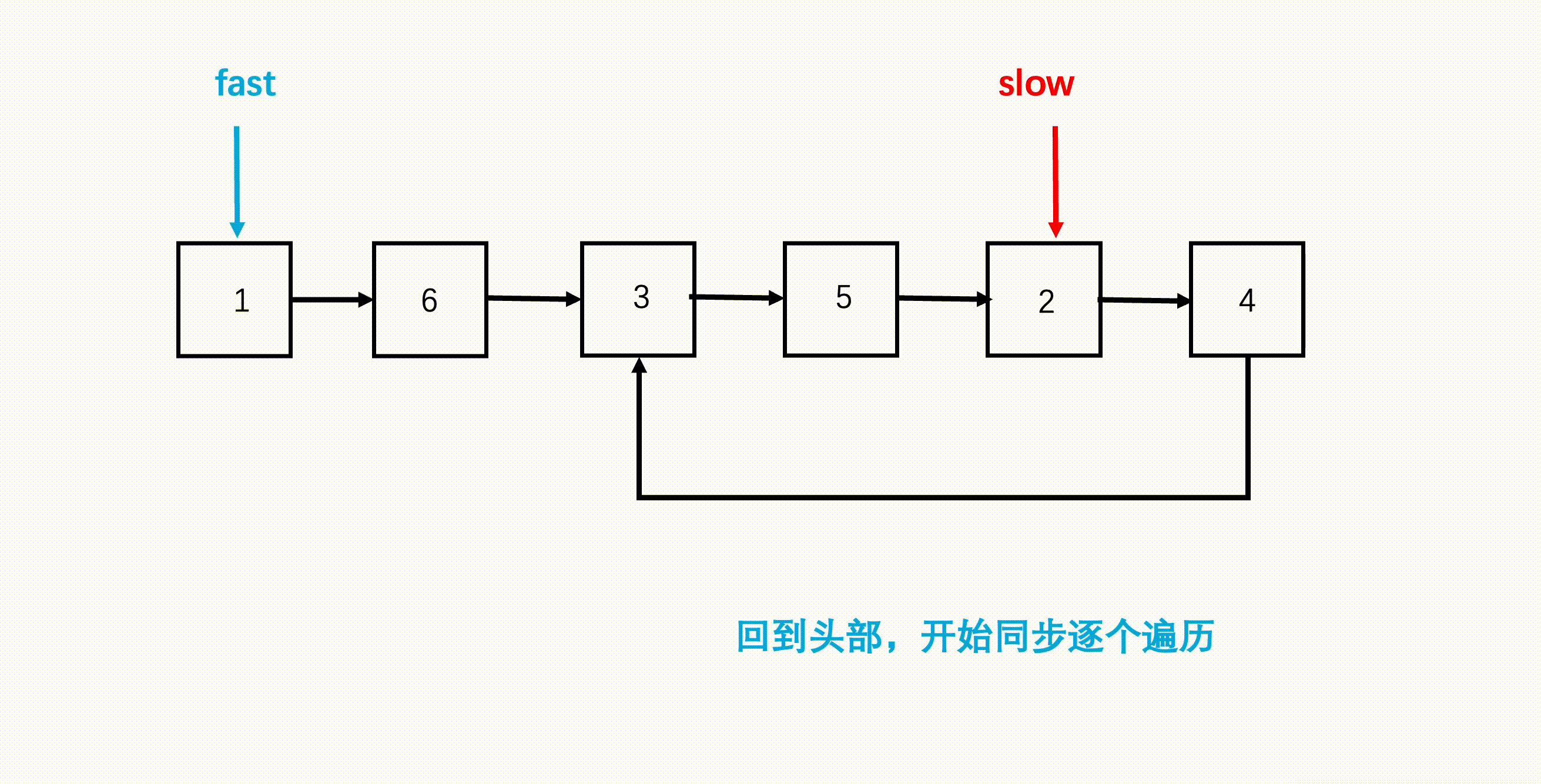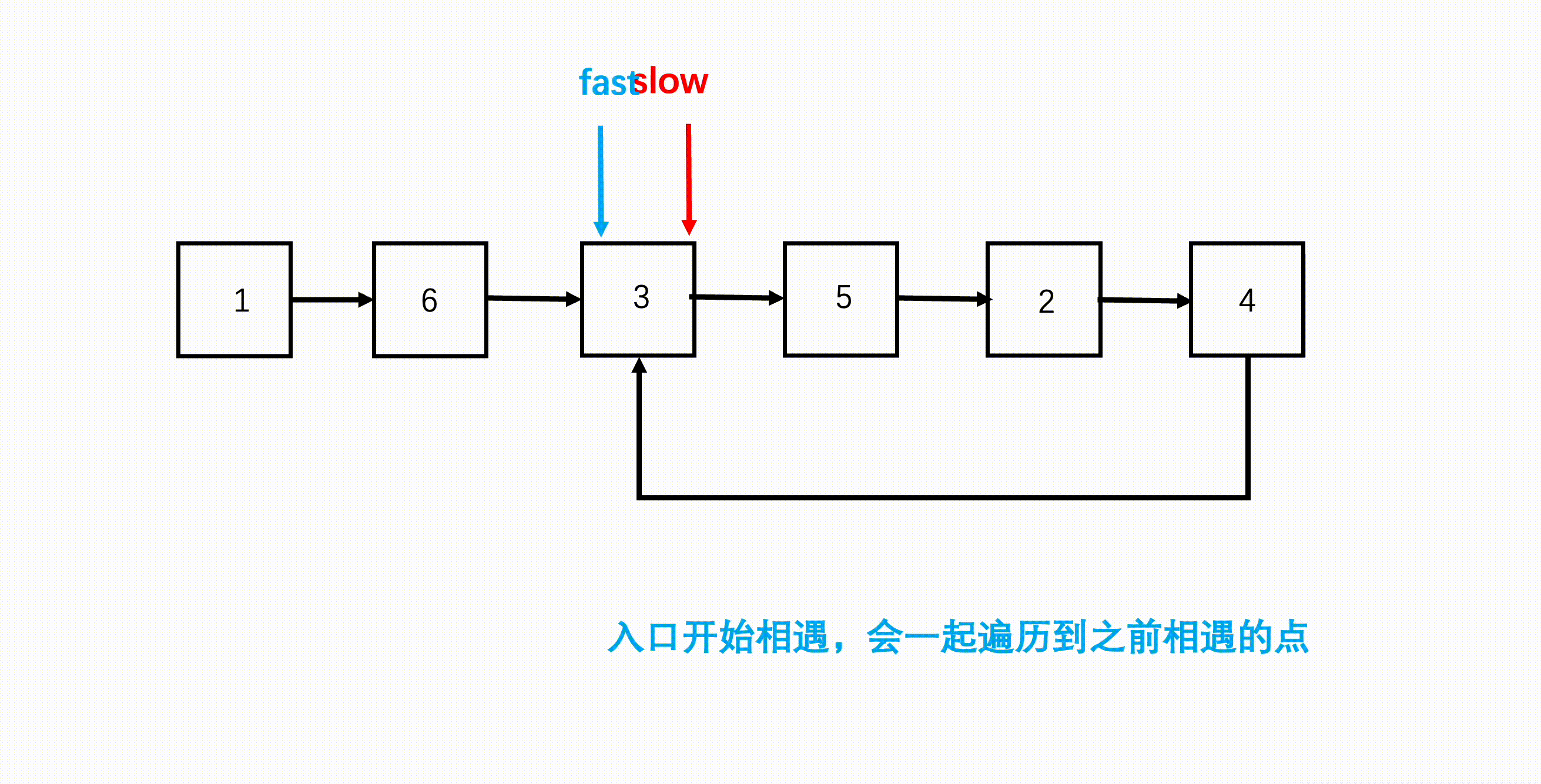
快慢指针找环入口节点

为什么这样就能找到环的入口节点了呢？

假设在一个有环链表中。快指针在环中走了 \(n\) 圈，慢指针走了 \(m\) 圈，两者相遇。此时，链表头节点到环入口点距离为 \(x\)，环入口到相遇点距离为 \(y\)，相遇点到环入口点距离为 \(z\)。

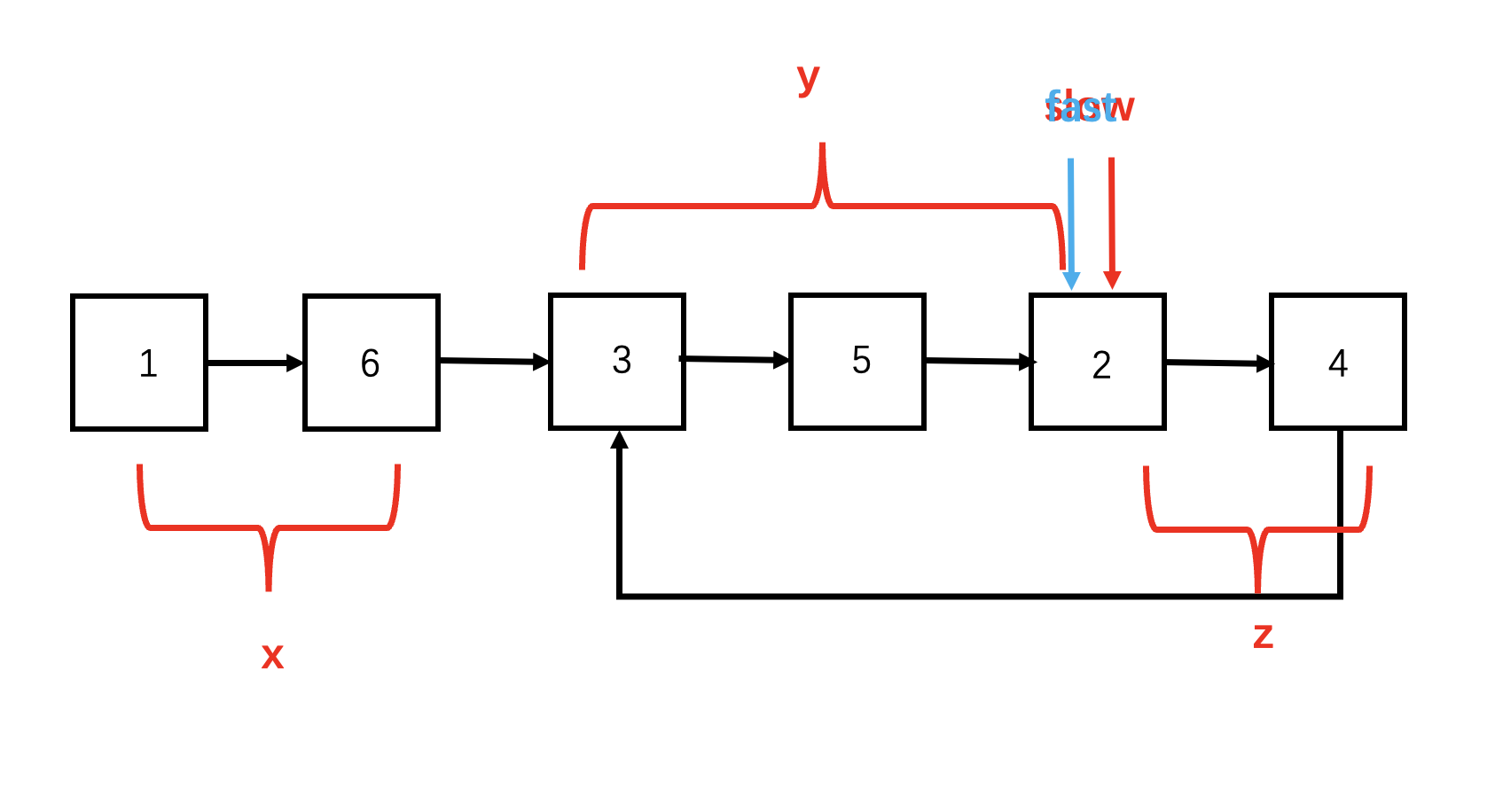
快慢指针相遇时，入口节点为3

这个过程中，快指针一共走了 \(x + n(y + z) + y\) 步，慢指针一共走了 \(x + m(y + z) + y\) 步。

快指针走的步数是慢指针的两倍，则 \[ x + n(y + z) + y = 2(x + m(y + z) + y) \] 进一步推导 \[ x+y=(n-2m)(y+z) \] \(y+z\) 就是环的大小，这说明从链表头经过环入口到达相遇地方经过的距离(x + y)等于整数倍环的大小(y + z)。

那么此时，我们从头开始遍历到相遇位置(x + y)，从相遇位置开始在环中遍历(y + z)，会使用相同的步数，而双方最后都会经过入口到相遇位置这 \(y\) 个节点，说明这 \(y\) 个节点它们就是重叠遍历的，那它们从入口位置就相遇了，这样就找到了入口节点。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public ListNode detectCycle(ListNode head) {
    // 判空
    if (head == null || head.next == null) {
        return null;
    }
    // 定义快慢双指针，初始化指向链表头节点 head
    ListNode fast = head, slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (slow == fast) { // 相遇跳出循环
            break;
        }
    }
    // 跳出循环有两种可能
    // 1. 快指针到末尾了，链表无环
    // 2. 链表有环，快慢指针相遇了
    // 情况 2
    if (fast != null && fast.next != null) {
        fast = head; // 快指针重新指向头结点
        // 快慢指针同步遍历链表，再次相遇的节点就是环入口节点
        while (fast != slow) { 
            fast = fast.next;
            slow = slow.next;
        }
        return fast;
    }
    // 情况 1
    return null;
}

时间复杂度

\(O(n)\)

最坏情况下遍历链表两次

空间复杂度

\(O(1)\)

使用了常数个指针，没有额外辅助空间

⭐️相交链表(力扣160)

题目描述

相交链表(力扣160)

这道题就是要寻找到两个链表的第一个公共节点。

思路(双指针)

我们使用两个指针 p1、p2 分别在链表 1、链表 2 上同步前进，但是无法同时走到公共节点。因此，解决这道题的关键在于，如何能够让两个指针同时到达相交节点 6。

两个指针的速度是一样的，那么如何才能同时到达相同点呢？那么应该要让两个指针走同样的长度。

因此，两个指针一起遍历，如果 p1 先遍历完链表 1 的话，就从链表 2 的头节点继续遍历。同样的，如果 p2 先遍历完链表 2 的话，就从链表 1 的头节点继续遍历。也就是说，p1 和 p2 都会遍历链表 1 和链表 2。

两个指针，同样的速度，走完同样的长度(链表 1 + 链表 2)，不管两条链表有无相同节点，都能够同时到达终点。

也就是说，如果有公共节点，两个指针一定会相遇，相遇节点就是第一个公共节点；如果没有公共节点，两个指针都会走到终点，此时都是 null，也算是相等了。

双指针确定两链表第一个公共节点

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    // 判空
    if (headA == null || headB == null) {
        return null;
    }
    // 初始化 p1 和 p2 两个指针，分别指向两个链表头
    ListNode p1 = headA, p2 = headB;
    while (p1 != p2) {
        // 如果 p1 不为空，前进一步，为空则从链表 B 头节点开始
        if (p1 != null) {
            p1 = p1.next;
        } else {
            p1 = headB;
        }
        // 如果 p2 不为空，前进一步，为空则从链表 A 头节点开始
        if (p2 != null) {
            p2 = p2.next;
        } else {
            p2 = headA;
        }
    }
    return p1;
}

时间复杂度

\(O(m+n)\)

链表 1 和链表 2 的长度之和。

空间复杂度

\(O(1)\)

常数级指针变量，无额外辅助空间使用。

链表反转类问题

⭐️反转链表(力扣206)

题目描述

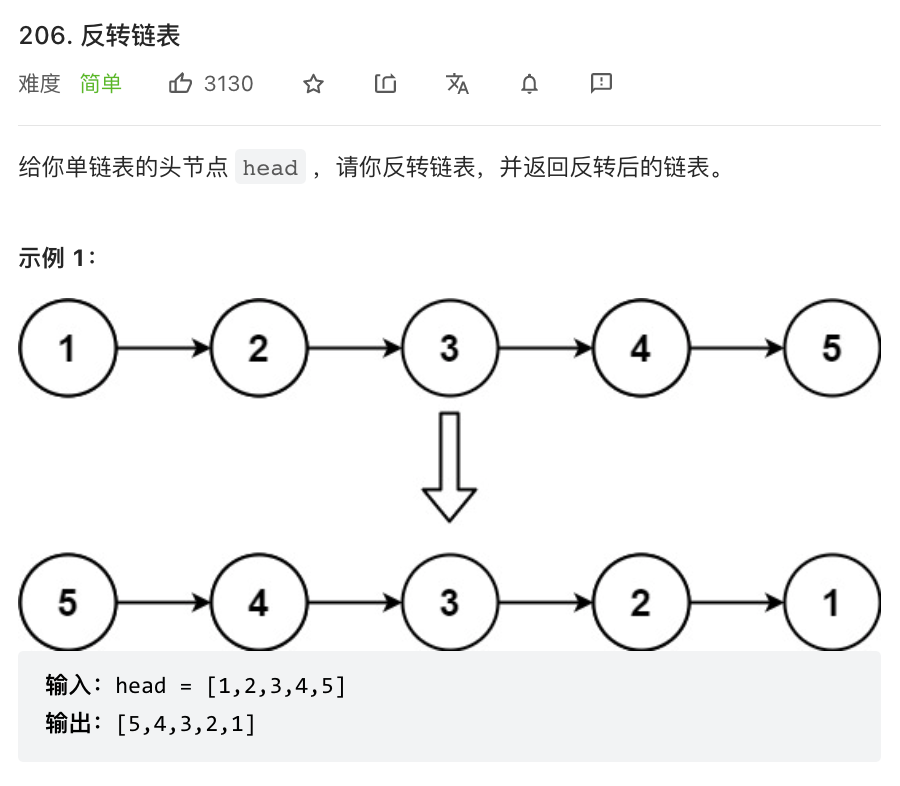
反转链表(力扣206)

思路(三指针)

反转链表一定要自己在纸上画一遍！

初始化三个指针分别是 pre(黄色)、cur(红色)、nxt(绿色)。

  • pre 指针用于指向已经反转好的链表的最后一个节点，最开始没有反转，所以为空。
  • cur 指针指向待反转链表(原链表)的第一个节点，最开始第一个节点待反转，所以指向 head。
  • nxt 指针指向待反转链表(原链表)的第二节点，用于保存链表，因为 cur 的 next 指针指向改变后，后面的链表就失效了，所以需要保存。
反转链表

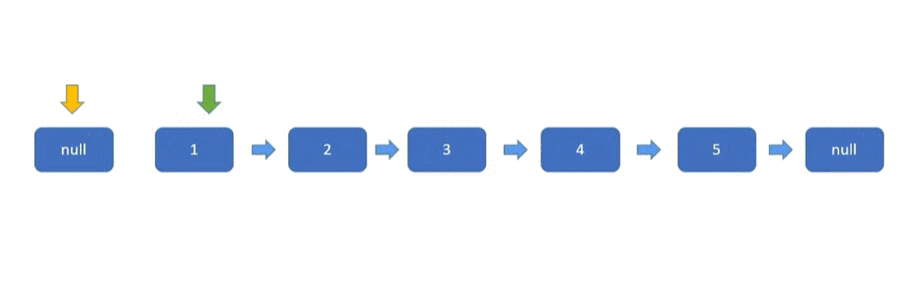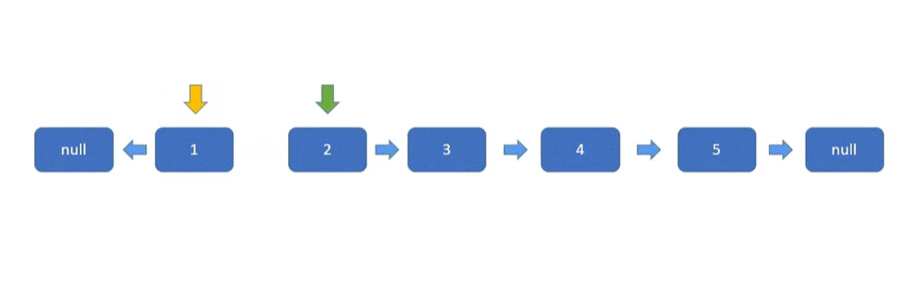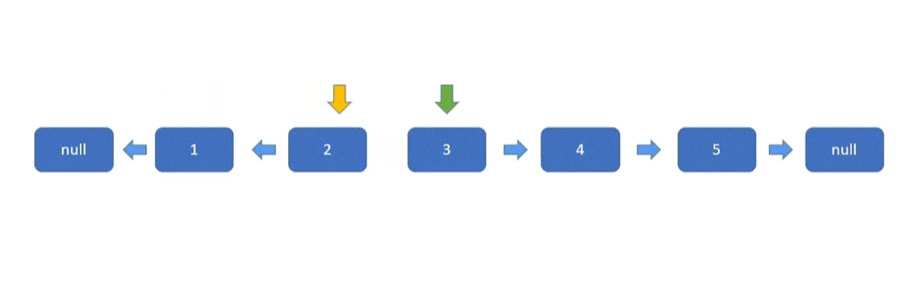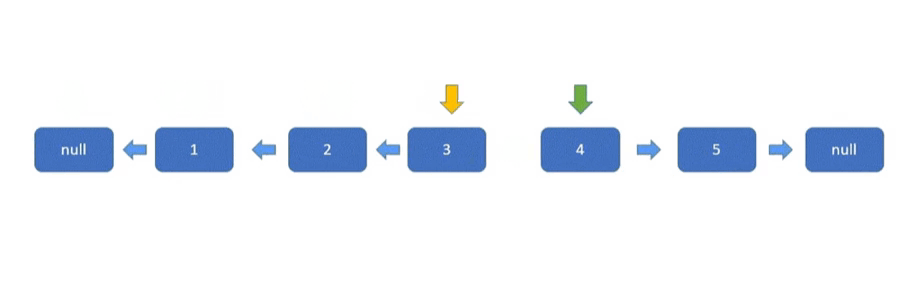
参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public ListNode reverseList(ListNode head) {
    if (head == null) {
        return head;
    }
    // 初始化三个指针
    ListNode pre = null, cur = head, nxt = null;
    while (cur != null) {
        nxt = cur.next; // 保存 cur 的下一个节点
        cur.next = pre; // 反转 
        // 指针后移，操作下一个未反转链表的第一个节点
        pre = cur; // 移动 pre 到 cur
        cur = nxt; // 移动 cur 到 nxt
    }
    // 返回反转后的头节点
    return pre;
}

时间复杂度

\(O(n)\)

最坏情况下，需要遍历整个链表。

空间复杂度

\(O(1)\)

常数级指针变量，无额外辅助空间使用。

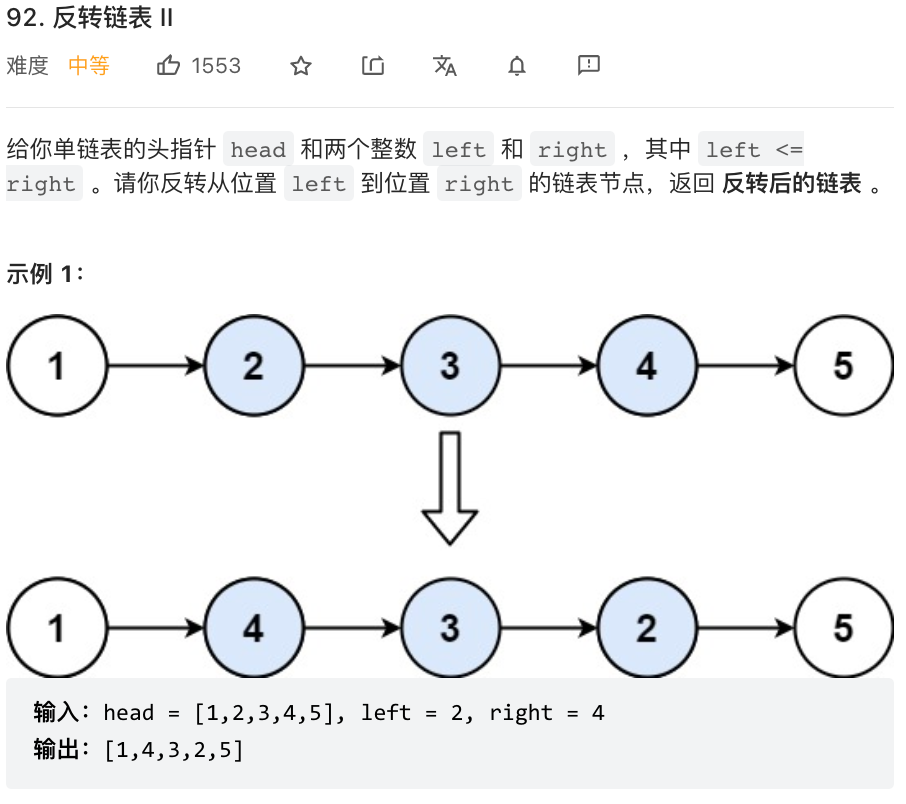
⭐️链表内指定区间反转(力扣92)

题目描述

指定区间反转(力扣92)

思路I(双指针)

先说最简单的一种方法，我们找到要反转的链表区间，将这个区间断开，然后利用上一道题的思路反转这个区间链表，然后再重新接上就可以了。这个部分的难点就是要记得保存好一些关键节点，待反转链表的前驱节点，后继节点，待反转链表自己的头节点。

反转指定区间的链表

参考代码I

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public ListNode reverseBetween (ListNode head, int m, int n) {
    if (head == null) {
        return null;
    }
    // 定义虚拟头节点，便于处理要删除链表第一个节点的情况
    ListNode dummy = new ListNode(-1);
    dummy.next = head;
    ListNode p = dummy;
    // 寻找第 m 个节点的前一个节点(待反转链表头节点的前驱节点)
    int i = 0;
    for (; i < m - 1; i++) {
        p = p.next;
    }
    // p 抵达第 m 个节点的前一个节点(待反转链表头节点的前驱节点)
    ListNode pre = p;
    // 寻找第 n 个节点
    for (; i < n; i++) {
        p = p.next;
    }
    // 保存第 n 个节点的下一个节点(待反转链表尾节点的后继节点)
    ListNode succ = p.next;
    // 切断待反转链表与后继节点的联系
    p.next = null;
    // 待反转链表的头节点
    ListNode reverseHead = pre.next;
    // 切断待反转链表头节点与前驱节点的联系
    pre.next = null;
    // 前驱节点连接反转后的链表
    pre.next = reverse(reverseHead);
    // 链表反转后，原来的头节点 reverseHead 变成了尾节点，连接后继节点
    reverseHead.next = succ;
    // 返回时去掉虚拟头节点
    return dummy.next;
}

ListNode reverse(ListNode head) {
    ListNode pre = null, nxt = null, cur = head;
    while (cur != null) {
        nxt = cur.next;
        cur.next = pre;
        pre = cur;
        cur = nxt;
    }
    return pre;
}

时间复杂度I

\(O(n)\)

遍历一次链表

空间复杂度I

\(O(1)\)

常数级指针变量，无额外辅助空间使用。

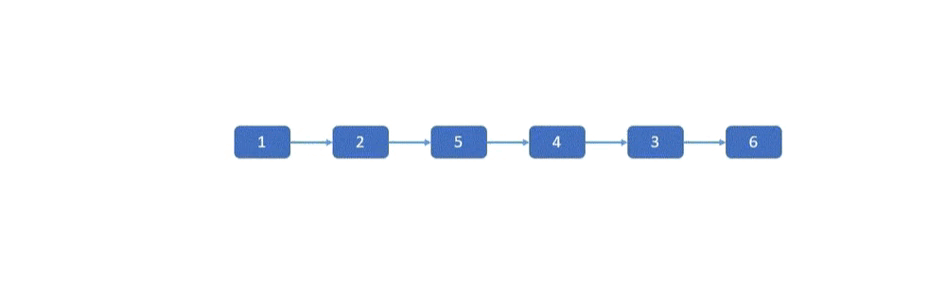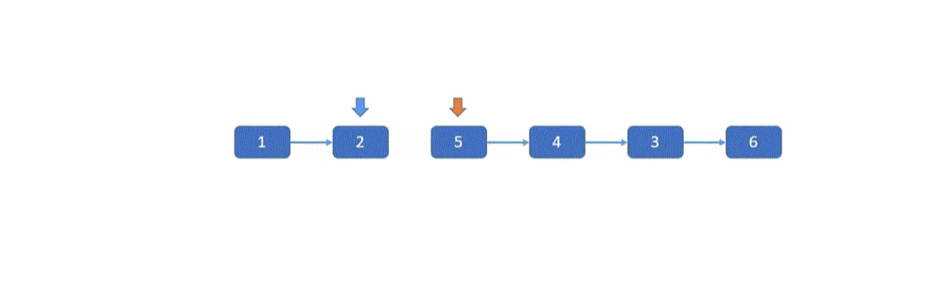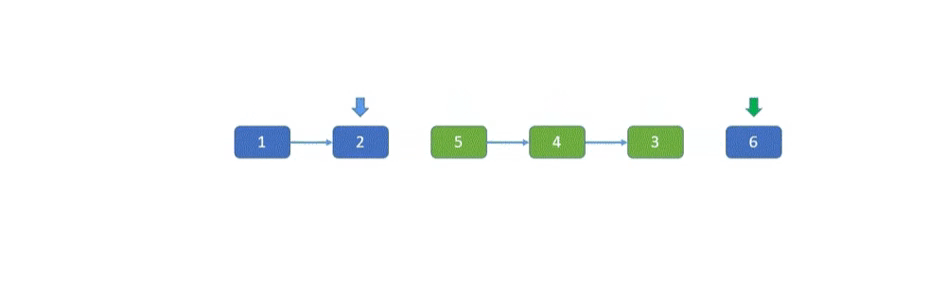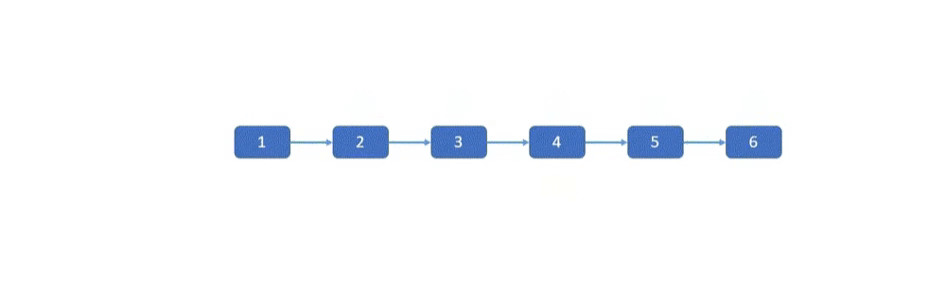
思路II(双指针头插迭代法)

一定要在纸上画一遍，肯定能够理解代码！

使用双指针，一个指向第 m 个节点，一个指向前驱节点(指针始终不变)。所谓头插法，以图示的 2 到 4 为例，先让 3 号节点插到 2 号节点前面，再让 4 号节点插到 3 号节点前面，这样就反转成功了。

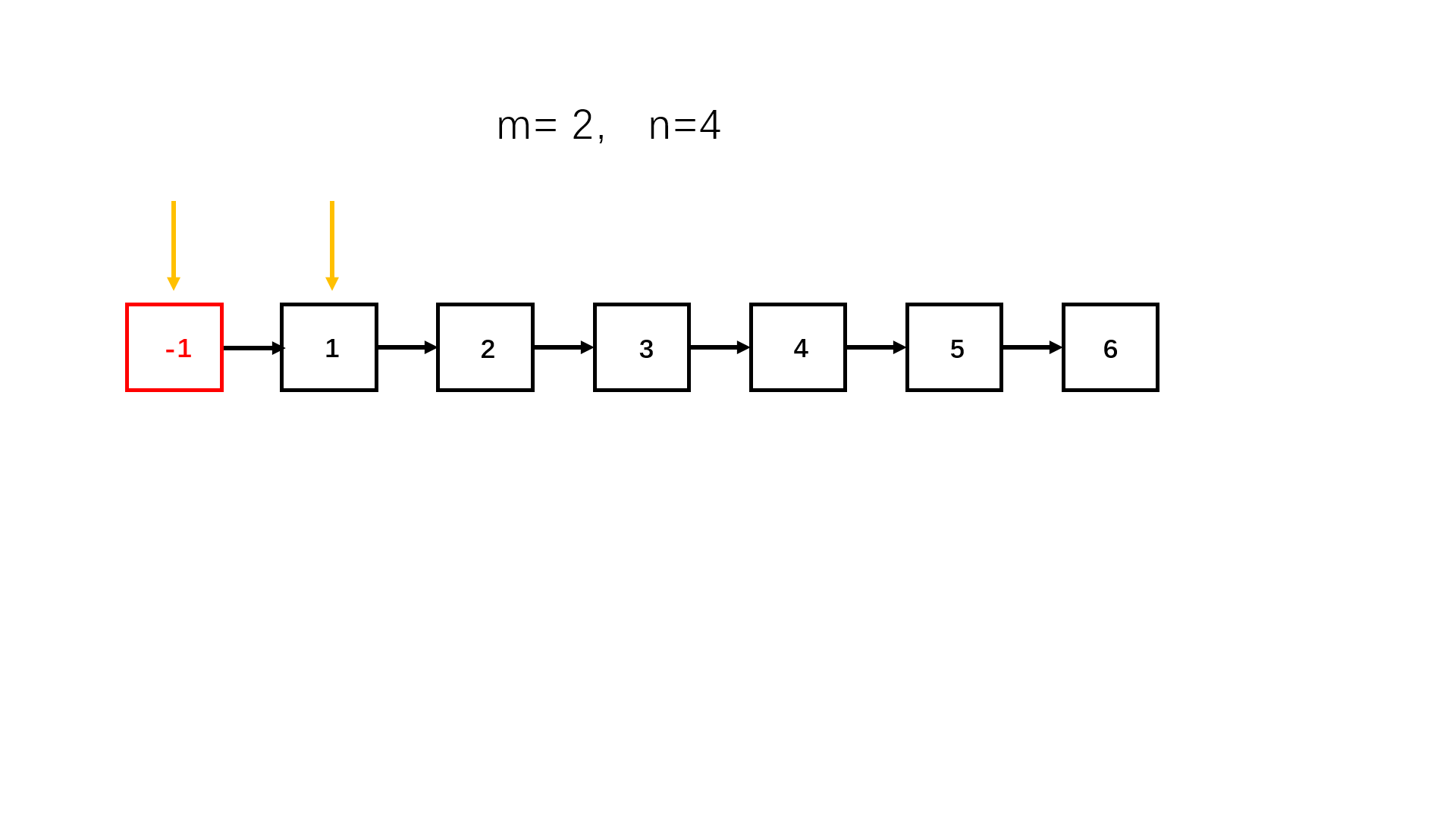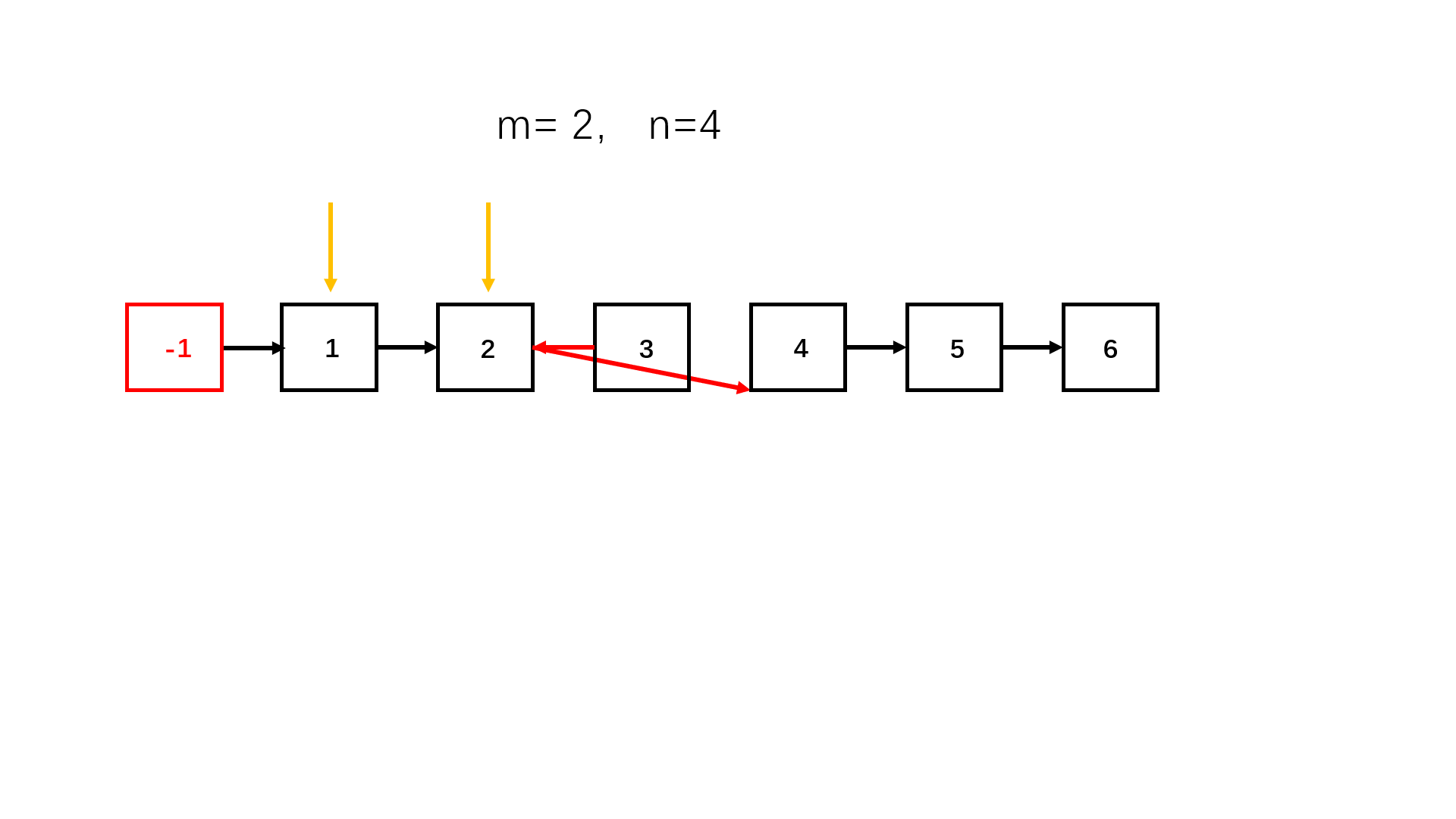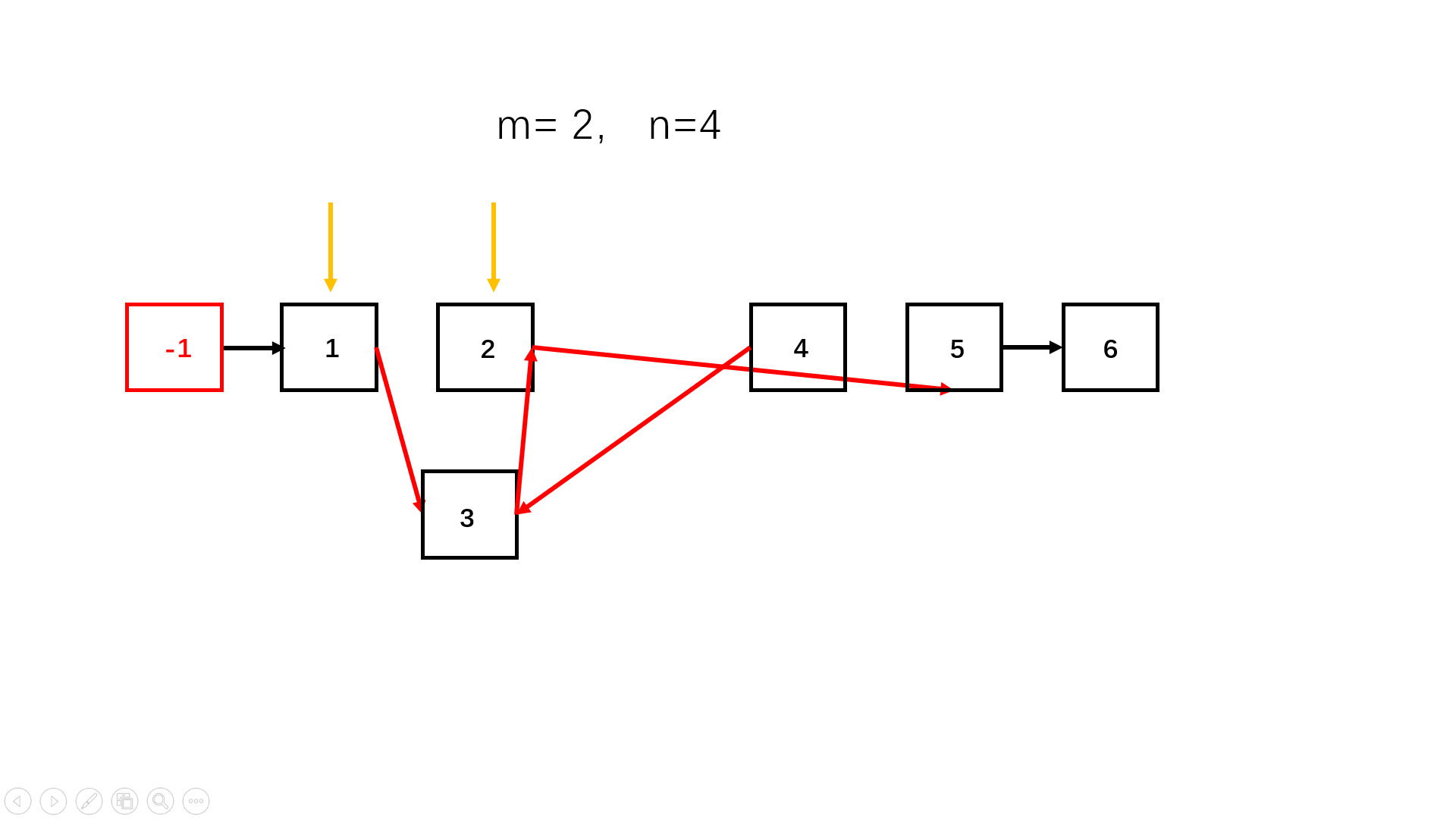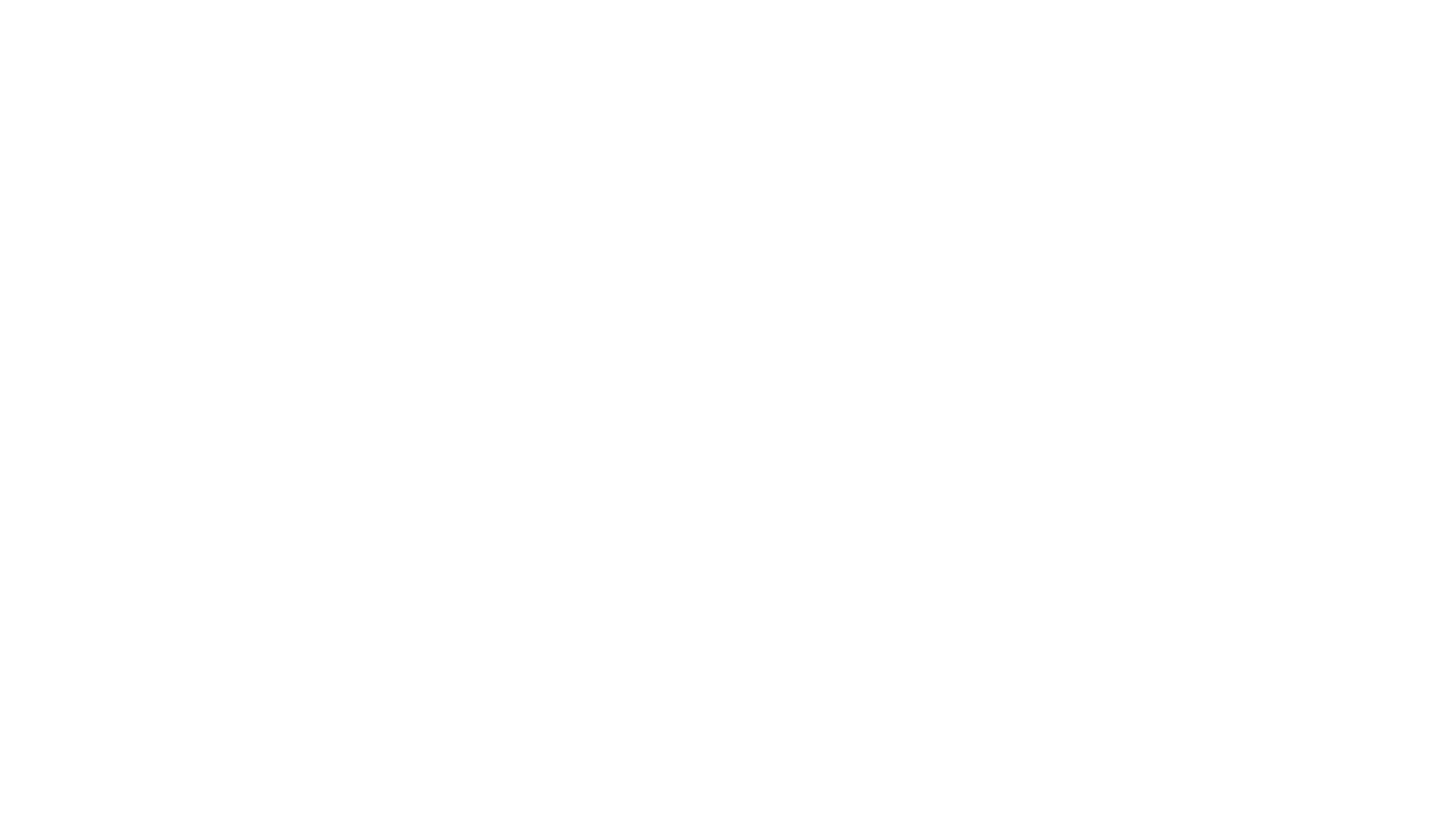
双指针头插迭代法

参考代码II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public ListNode reverseBetween (ListNode head, int m, int n) {
    ListNode dummy = new ListNode(-1);
    dummy.next = head;
    ListNode pre = dummy; // 永远指向待反转区域的头结点的前驱节点(前一个节点)，循环中永远不变
    // 找到第 m 个节点的前驱节点
    for (int i = 0; i < m - 1; i++) {
        pre = pre.next;
    }
    ListNode cur = pre.next; // 指向待反转区间的头结点
    ListNode nxt; // 永远指向 cur 节点的下一个节点
    for (int i = m; i < n; i++) {
        nxt = cur.next;
        // 当前节点的下一个节点要前插
        cur.next = nxt.next; // 当前节点的 next 要连接 nxt 的下一个节点 
        nxt.next = pre.next; // nxt 节点，前插到头部，连接原本的头结点(前驱节点的下一个节点)
        pre.next = nxt; // 前驱节点连向 nxt 节点
    }
    // 返回时去掉虚拟头节点
    return dummy.next;
}

时间复杂度II

\(O(n)\)

最坏情况下，遍历整个链表。

空间复杂度II

\(O(1)\)

常数级指针变量，无额外辅助空间使用。

K 个一组翻转链表(力扣25)

题目描述

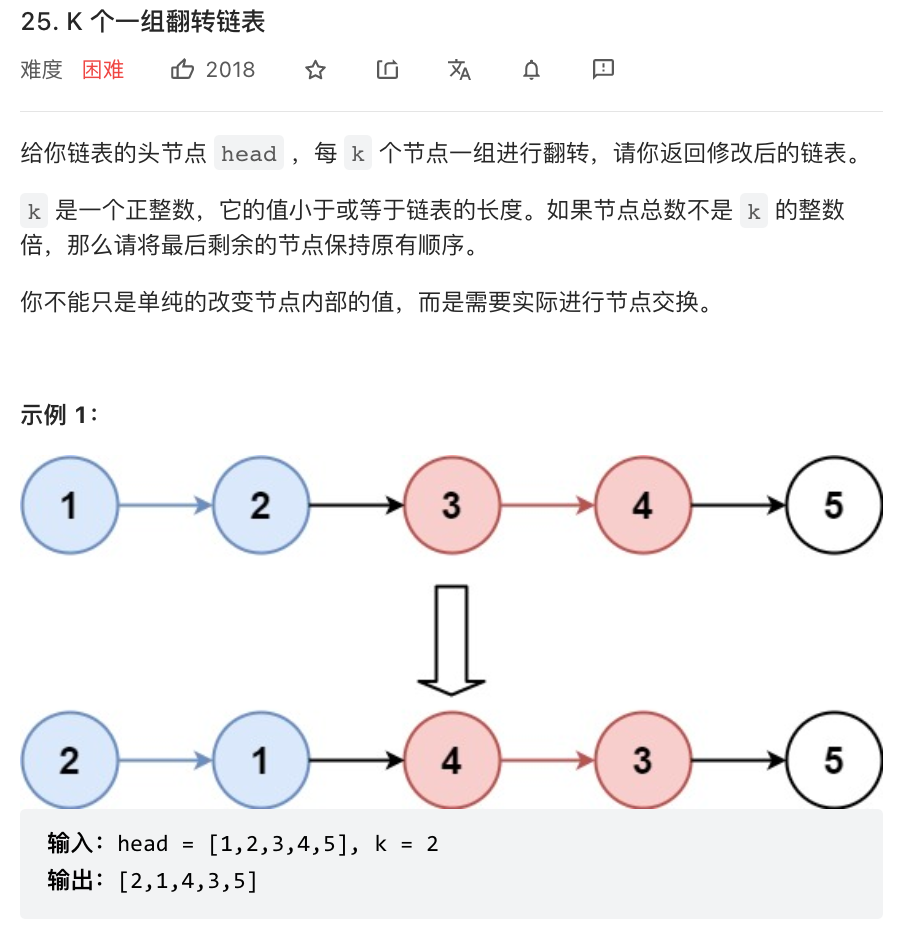
K 个一组翻转链表(力扣25)

思路(双指针+递归)

这道题思路很简单，我们只要每轮遍历链表 k 次，分出一组，不足 k 次，不用翻转直接返回这一组的头节点即可。

分出一组后，对这组链表进行翻转，原来的头变成了尾，然后拼接在一起就可以啦。

如何翻转 k 个链表节点呢？

还记得我们之前做过的「反转链表」题目吗？题目的函数签名是 ListNode reverseList(ListNode head)，这个可以理解为「反转 head 到 null 之间的节点」。

1
2
3
4
5
6
7
8
9
10
public ListNode reverseList(ListNode head) {
    ListNode pre = null, cur = head, succ = null;
    while (cur != null) {
        succ = cur.next;
        cur.next = pre;
        pre = cur;
        cur = succ;
    }
    return pre;
}

那么如果要翻转 head 到 tail 之间的节点(一共 k 个节点)，要如何做呢？

我们只要更改函数签名 ListNode reverseList(ListNode head, ListNode tail)，将原本代码中的 null 改为 tail 即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
// 反转 [head, tail) 的链表节点
public ListNode reverseList(ListNode head, ListNode tail) {
    ListNode pre = null, cur = head, succ = null;
    // 终止条件从 null 变成 tail
    while (cur != tail) {
        succ = cur.next;
        cur.next = pre;
        pre = cur;
        cur = succ;
    }
    // 返回反转后的头节点
    return pre;
}

完整过程如下。

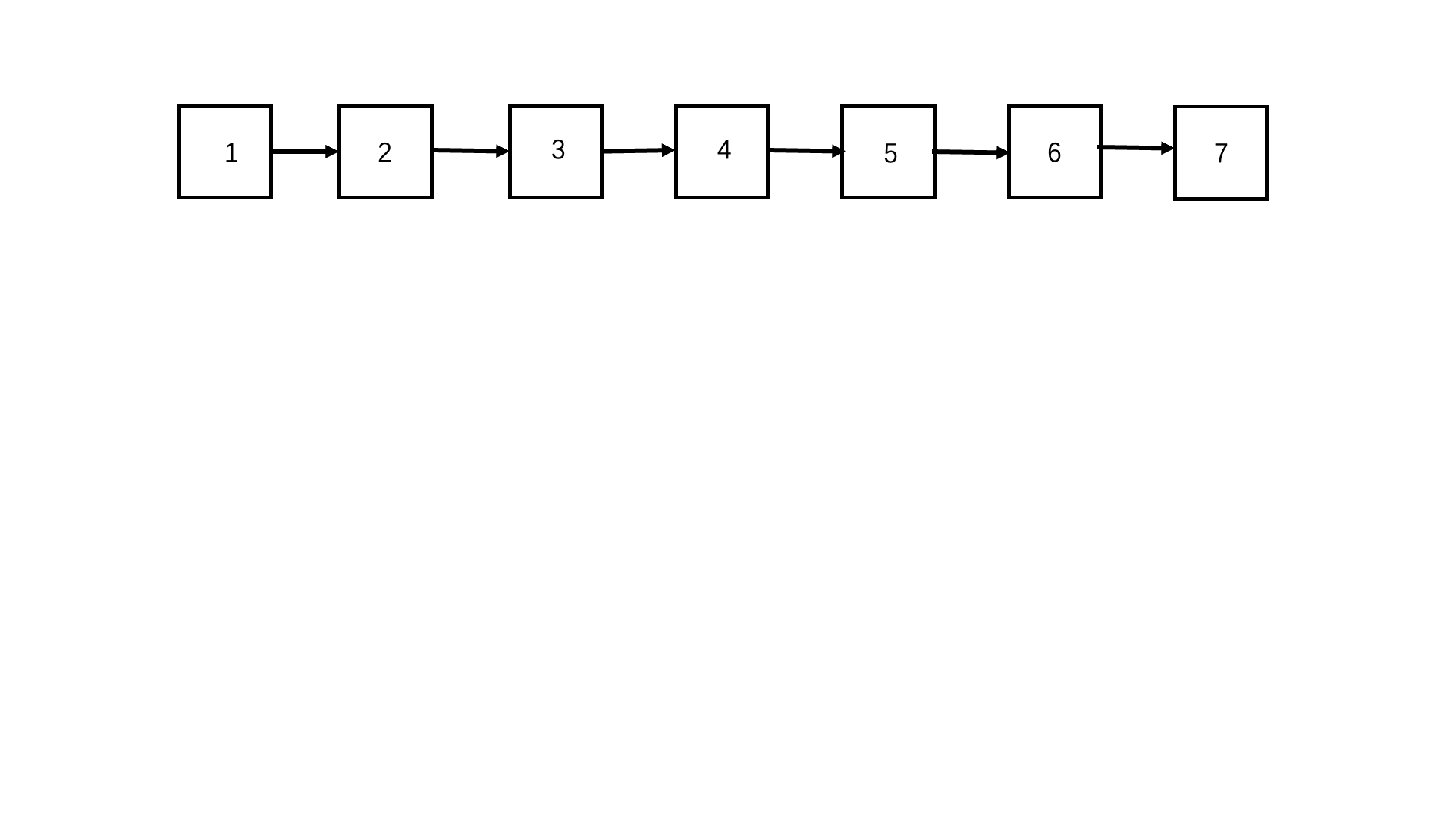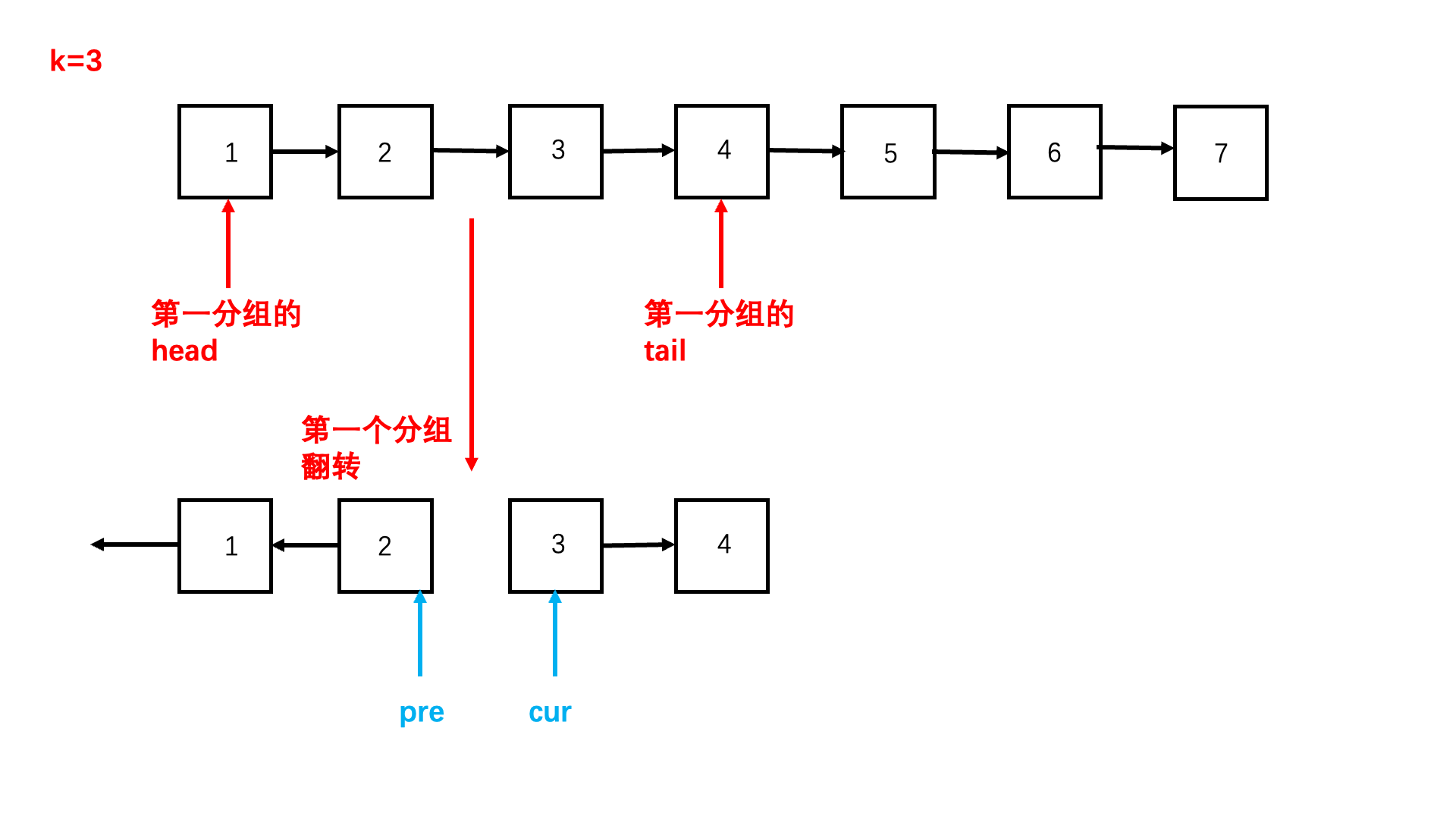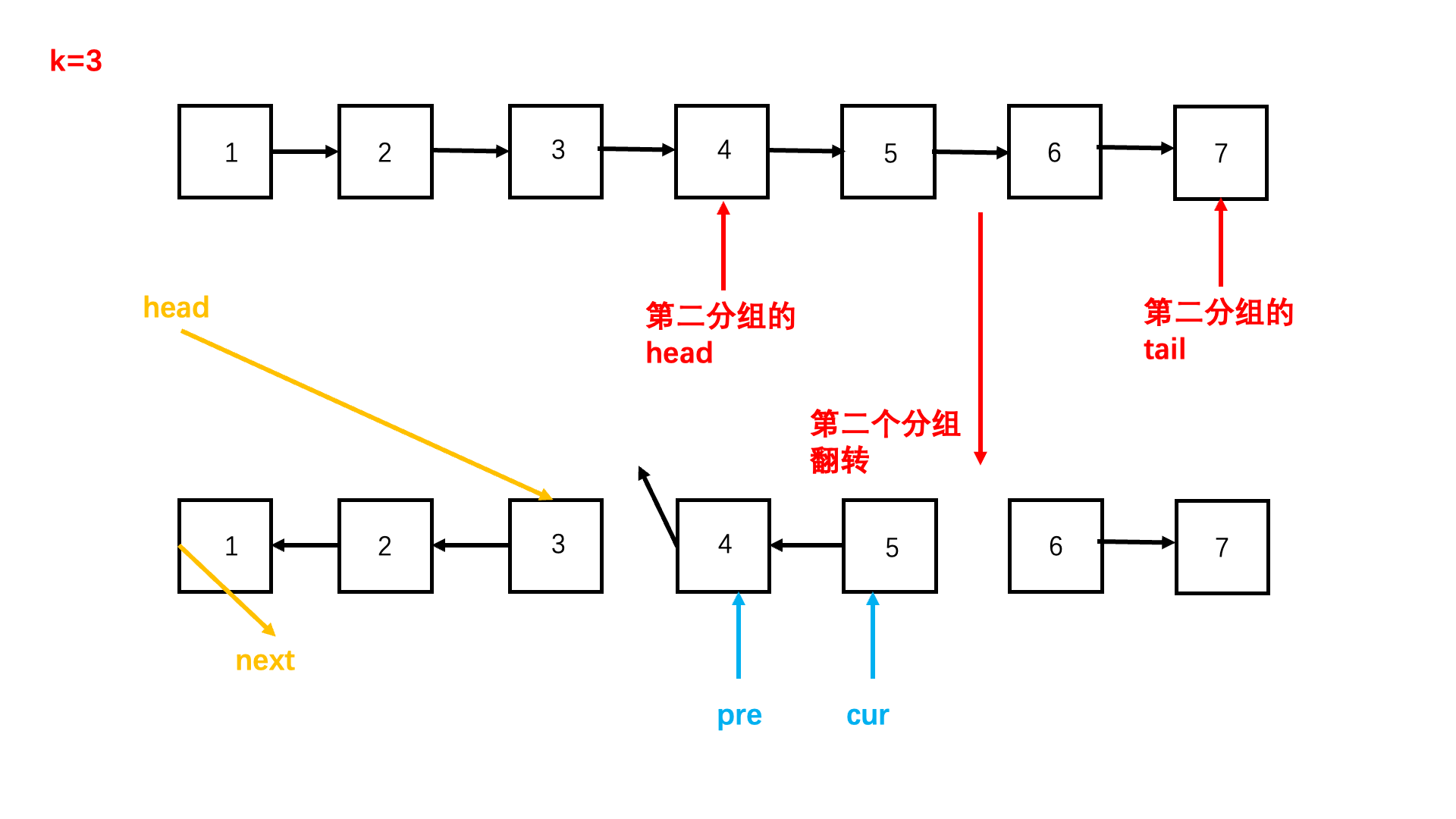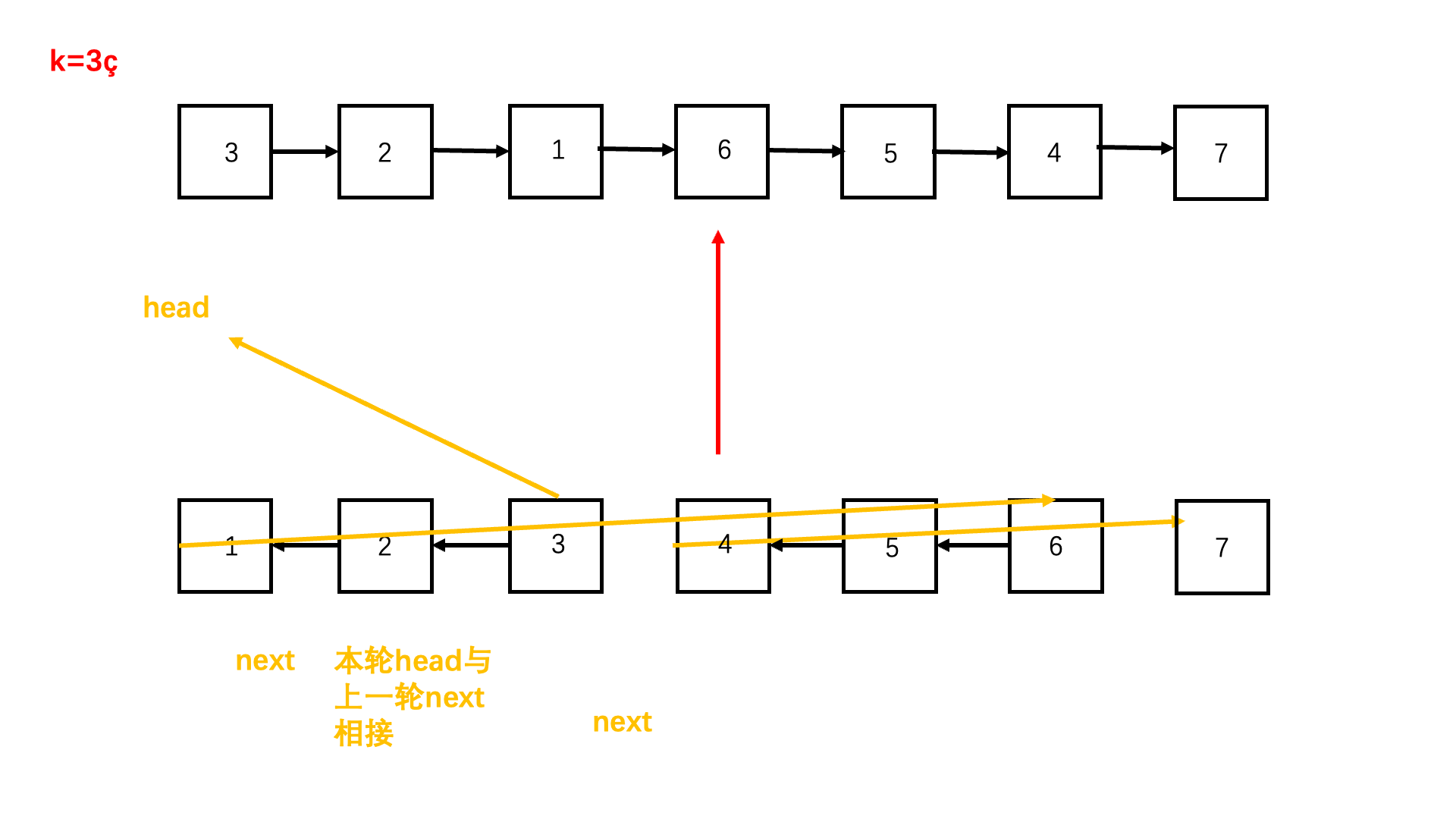
K 个一组反转链表

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public ListNode reverseKGroup(ListNode head, int k) {
    if (head == null) {
        return head;
    }
    // 区间 [pHead, pTail) 有 k 个待反转的节点
    ListNode pHead = head, pTail = head;
    // 让 pTail 指向第 k 个节点
    for (int i = 0; i < k; i++) {
        // 不足 k 个节点，不需要反转，base case
        if (pTail == null) {
            return head;
        }
        pTail = pTail.next;
    }
    // 反转 k 个节点 
    ListNode newHead = reverseList(pHead, pTail);
    // 递归反转后续链表并连接起来
    pHead.next = reverseKGroup(pTail, k);
    return newHead;
}

// 反转 [head, tail) 的链表节点
public ListNode reverseList(ListNode head, ListNode tail) {
    ListNode pre = null, cur = head, succ = null;
    // 终止条件从 null 变成 tail
    while (cur != tail) {
        succ = cur.next;
        cur.next = pre;
        pre = cur;
        cur = succ;
    }
    // 返回反转后的头节点
    return pre;
}

代码中 for 循环之后的部分可能需要再解释一下，如图所示：

递归反转并连接后的样子如下：

时间复杂度

\(O(n)\)

遍历链表所有节点

空间复杂度

\(O(n)\)

递归栈最大深度为 \(n/k\)

更新日志

更新时间 更新内容
2023.05.06 发布文章，详解双指针技巧，详解 9 道大厂常见手撕题目：合并两个有序链表、分割链表、合并 K 个升序链表、删除链表的倒数第 N 个节点、链表的中间节点、环形链表、环形链表的入口节点、相交链表、反转链表。
2023.05.09 新增题目：奇偶链表(力扣328)、指定区间反转(力扣92)。
2023.05.10 新增食用指南；新增题目：K 个一组翻转链表(力扣25)、回文链表(力扣234)。
2023.05.11 修改：更新回文链表(力扣234)图示。
2023.05.20 修改：对所有题目进行分类；修改标题级别。

参考资料

  1. 牛客网
  2. 力扣网
  3. 算法基地 - github
  4. labuladong 的算法小抄
  5. 代码随想录
  6. draw.io