基于算法(4th)单词查找树的改进

发表于 更新于 分类于 ， ， 本文字数： 5.1k 阅读时长 ≈ 19 分钟 阅读次数：

Trie 树，又名字典树、前缀树、单词查找树，是一种二叉树衍生出来的高级数据结构，主要应用场景是处理字符串前缀相关的操作。

本文在《算法(4th)》的单词查找树的基础上，参考《labuladong 的算法小抄》与《程序员代码指南》对其进行改进。

注意：

由于 Trie 树原理，我们要求 TrieMap 的键必须是字符串类型，值的类型 V 可以随意。

Trie 树原理

Trie 树本质上就是一棵从二叉树衍生出来的多叉树。

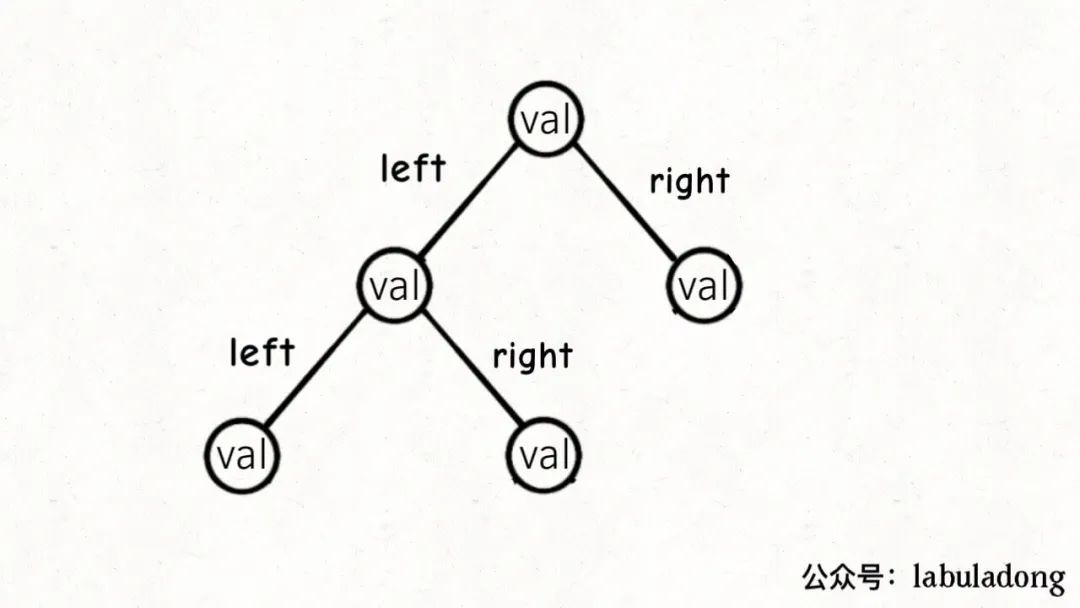
二叉树

1
2
3
4
5
// 基本二叉树节点
class TreeNode {
    int val;
    TreeNode left, right;
}

二叉树结构

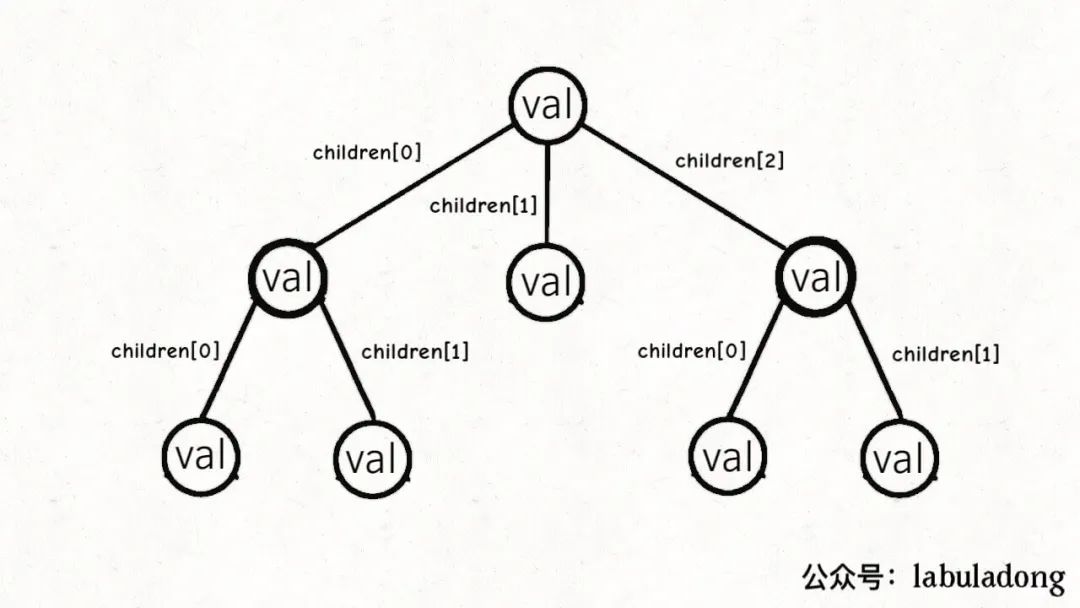
多叉树

1
2
3
4
5
// 基本多叉树节点
class TreeNode {
    int val;
    TreeNode[] children;
}

其中 children 数组中存储指向孩子节点的指针。

多叉树结构

前缀树

TrieNode 代码

TrieMap 中的树节点 TrieNode 的代码实现：

1
2
3
4
5
6
7
// Trie 树节点的实现
class TrieNode<V> {
    V val = null; // 键存储对应的值
    int pass; // 表示有多少个单词共用这个节点
    int end; // 表示有多少个单词以这个节点结尾
    HashMap<Character, TrieNode<V>> children; // key 代表该节点一条字符路径，value 表示字符路径指向的节点
}

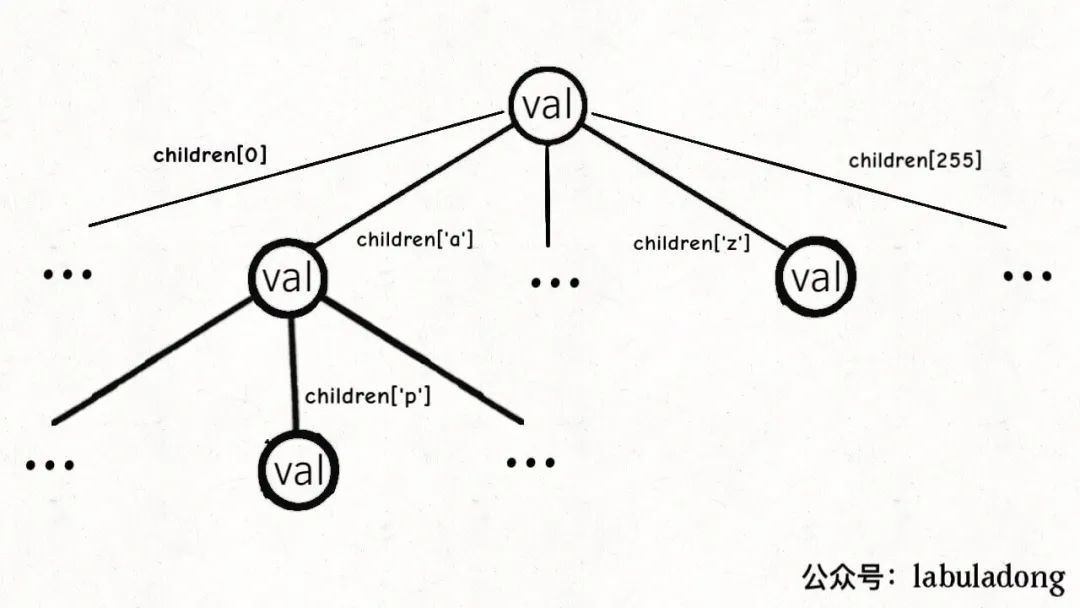
HashMap<Character, TrieNode<V>> children，也可以使用数组TrieNode<V>[] children来替代，比如长度为 256 的数组或者长度为 26 的数组，索引代表字符的 ASCII 码值。

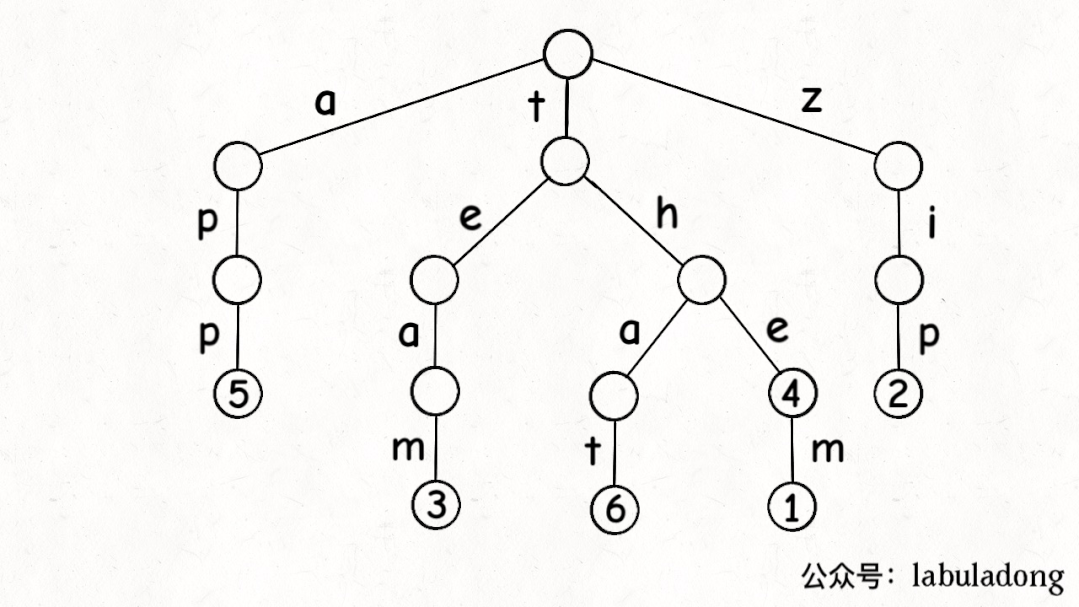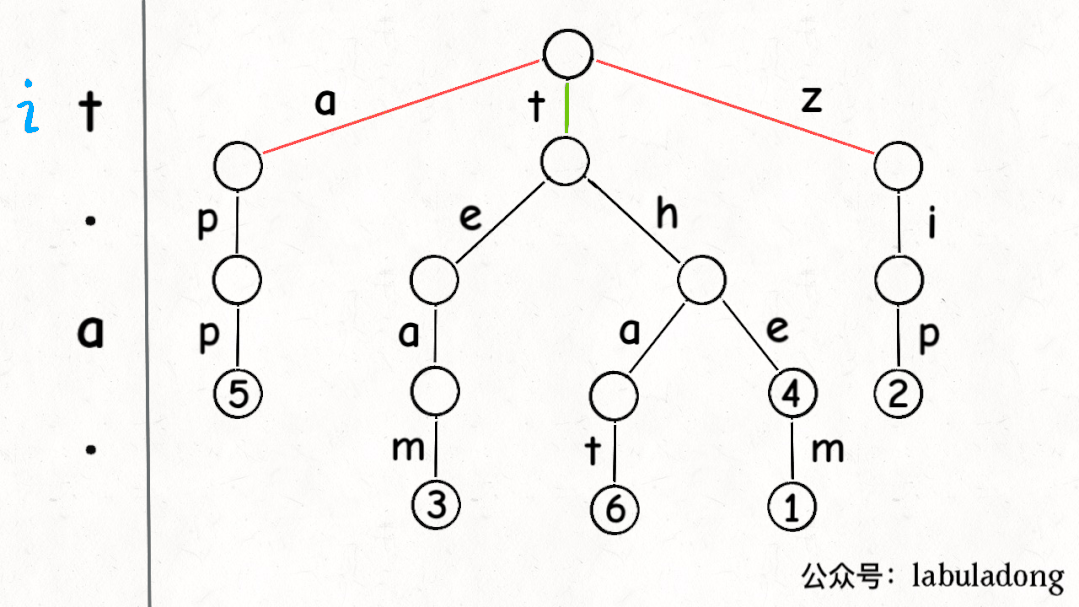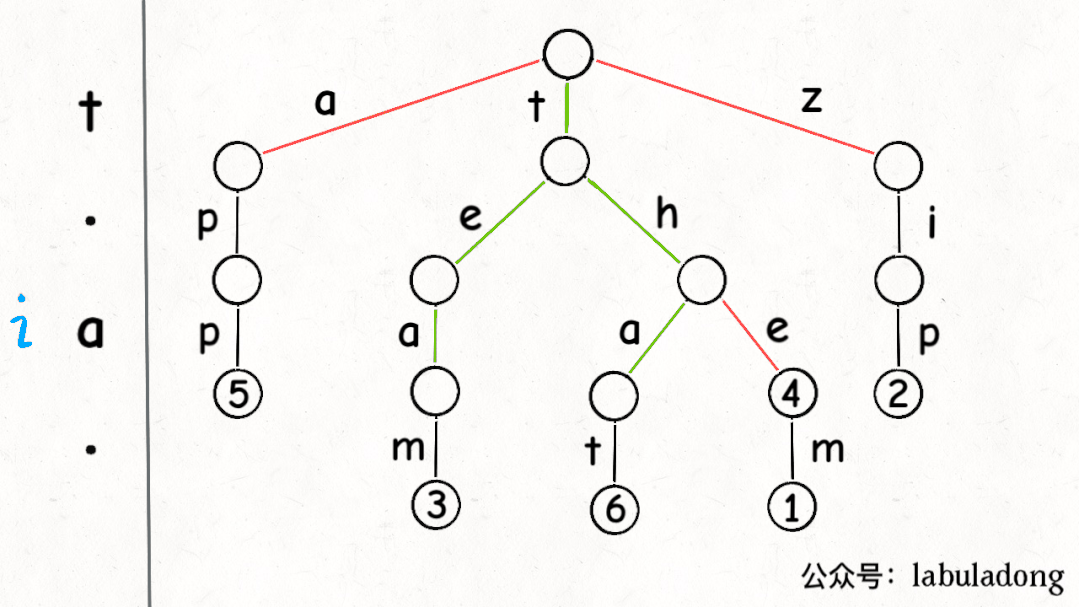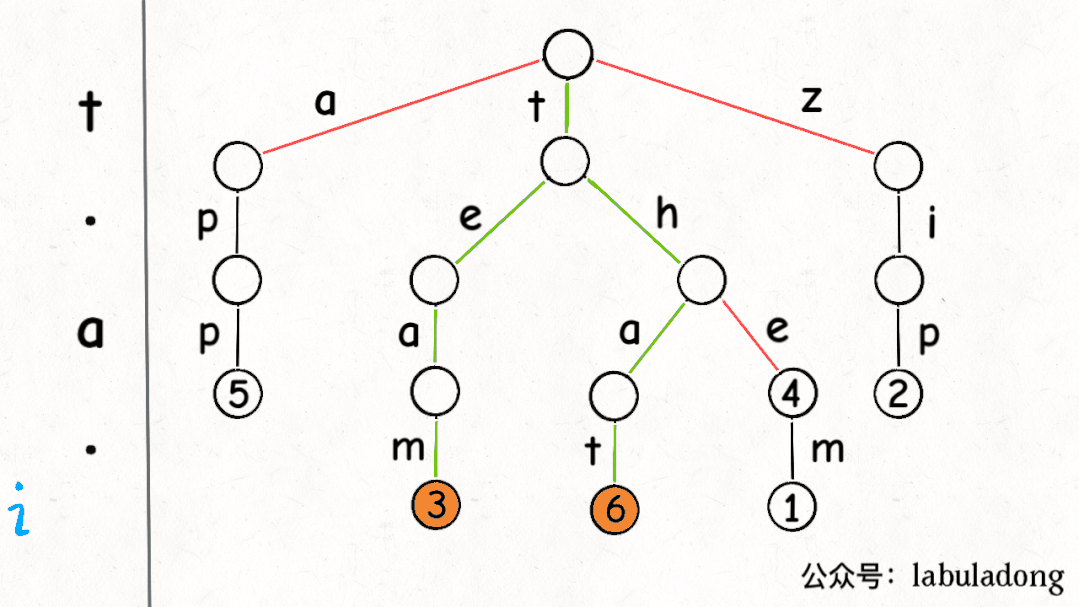
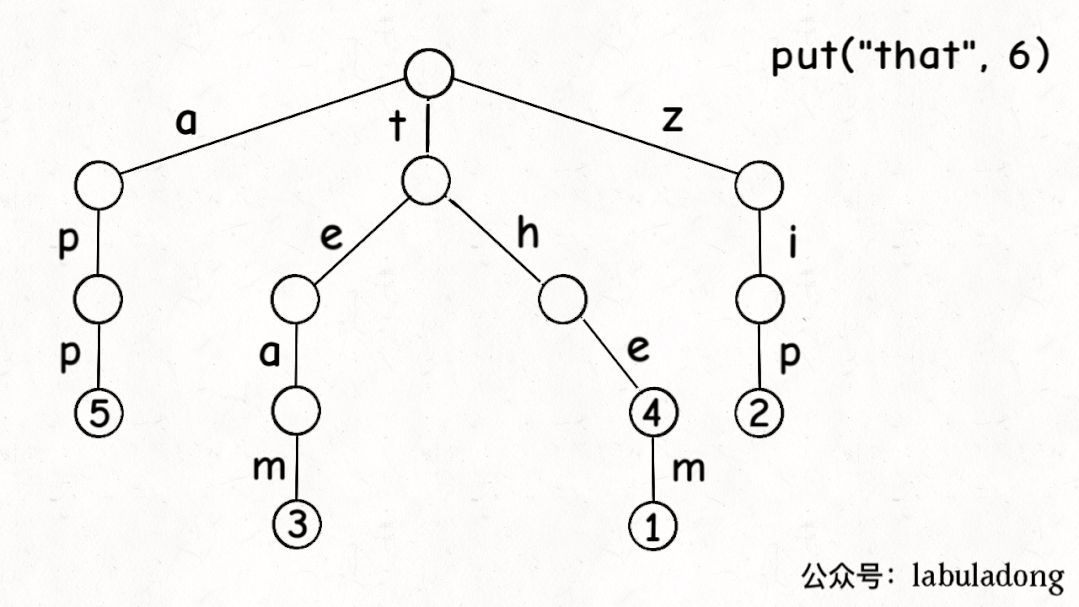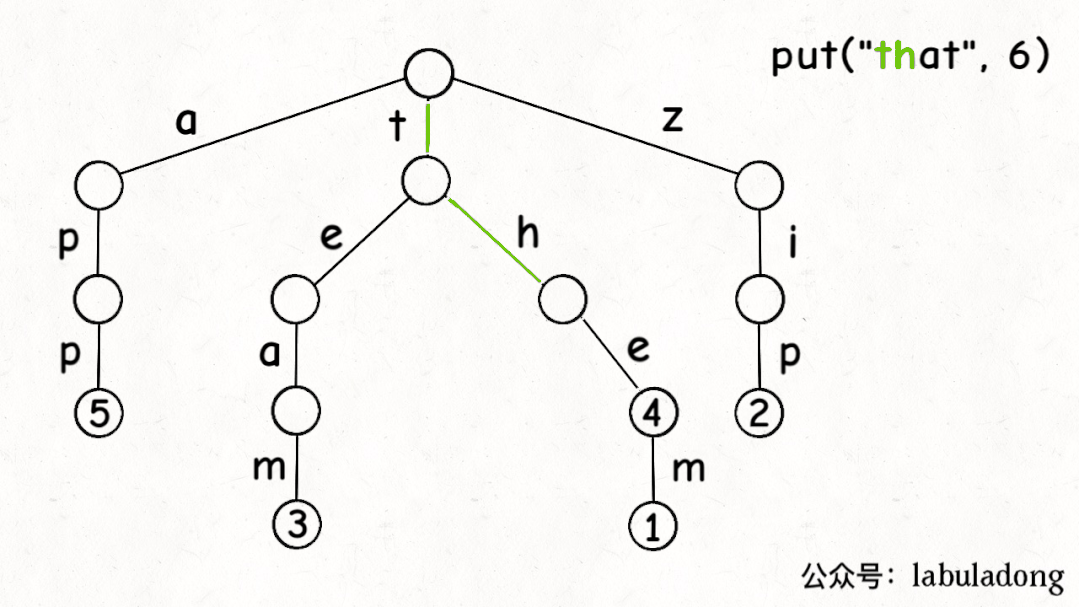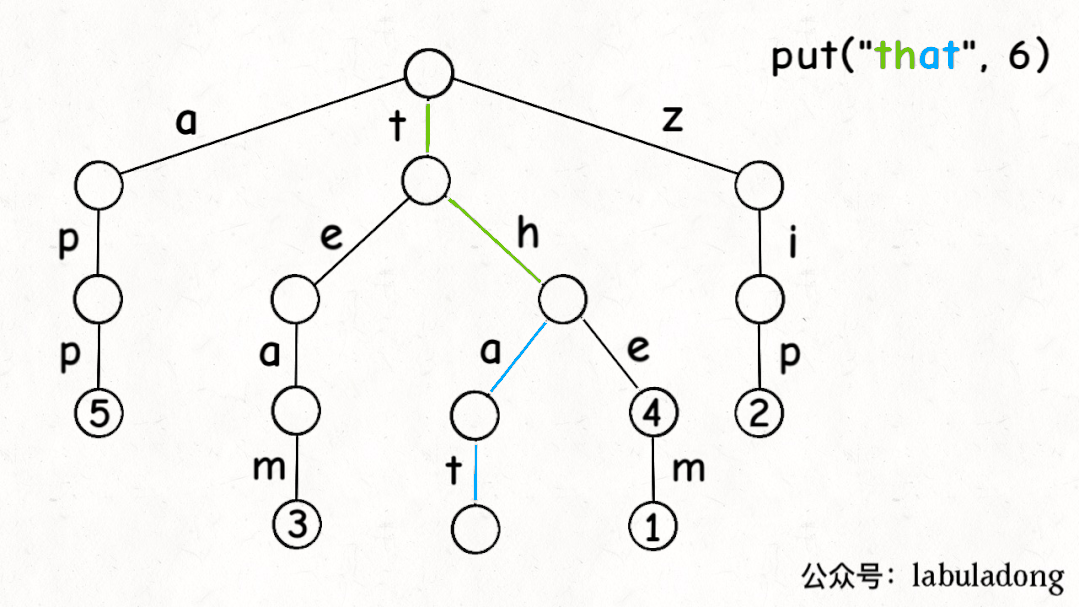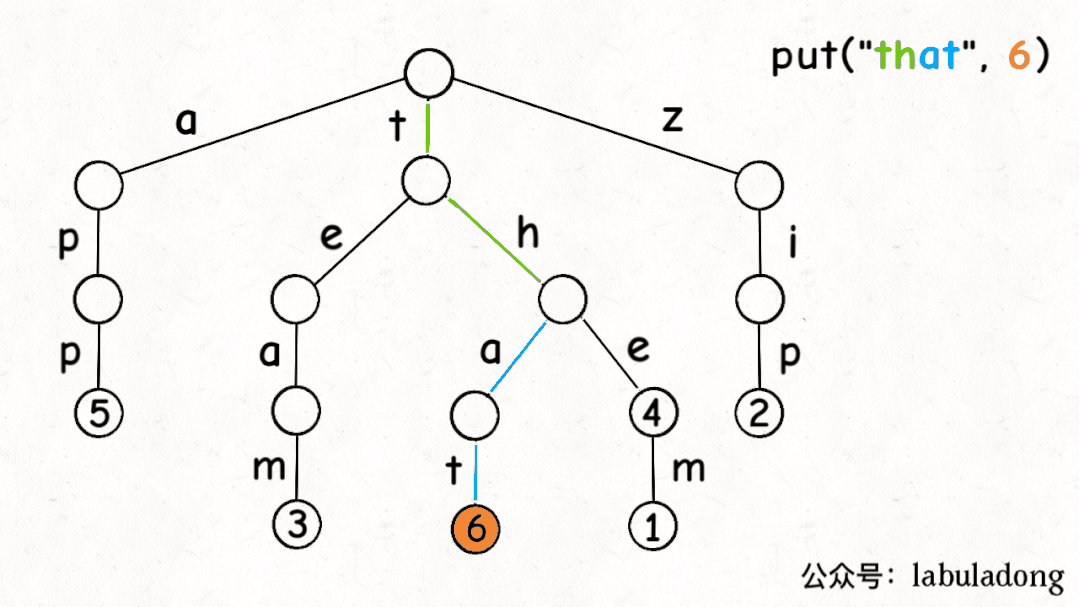
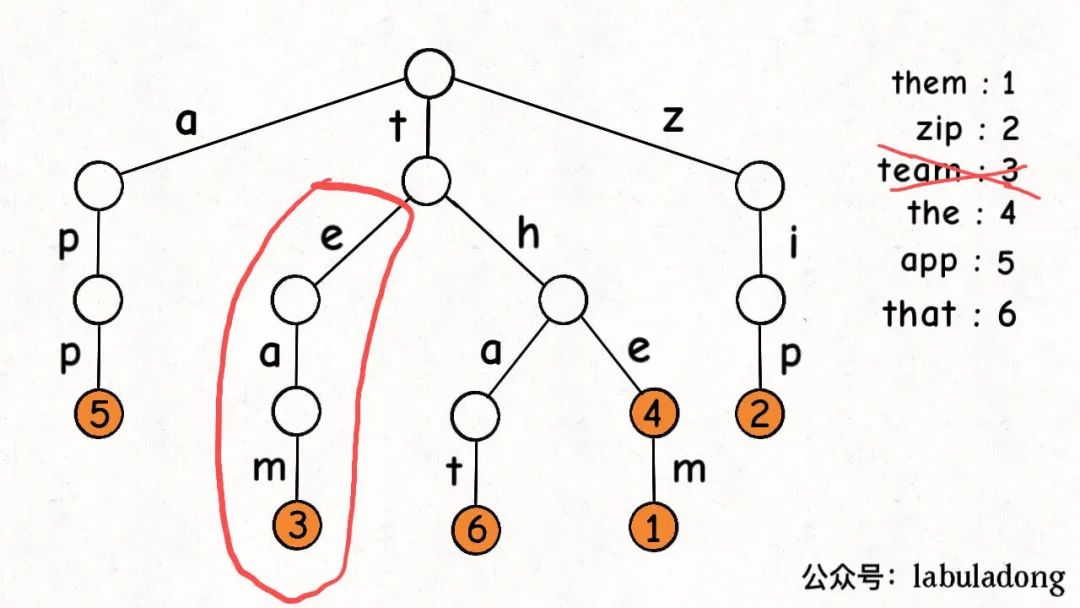
Trie 树结构图

Trie 树动画网站

Trie 树的结构

一个节点有 256 个子节点指针，但大多数时候都是空的，可以省略掉不画，所以一般看到的 Trie 树是这个样子：

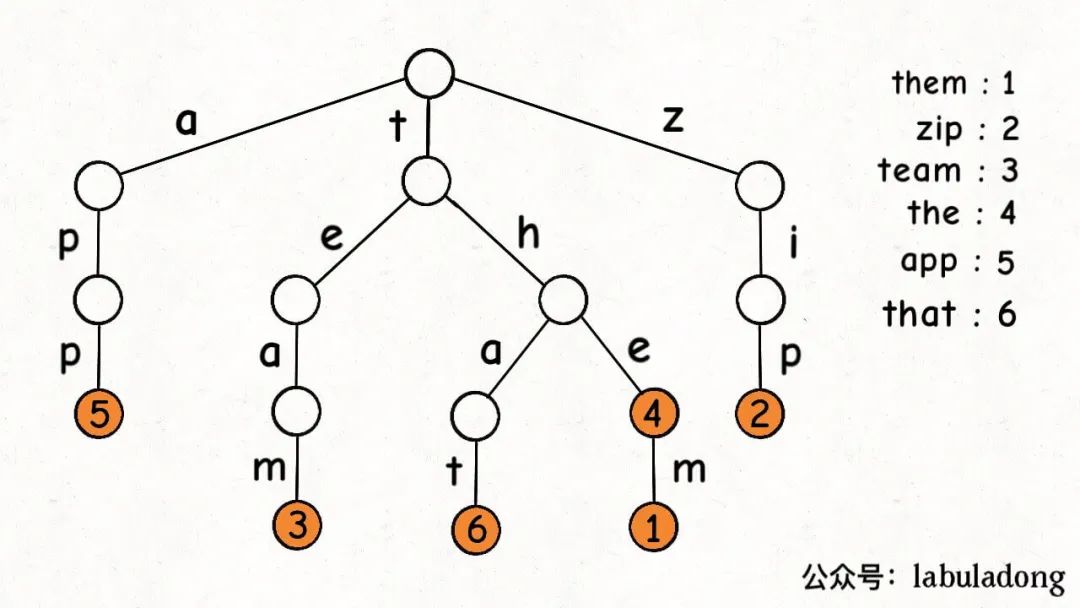
Trie 树

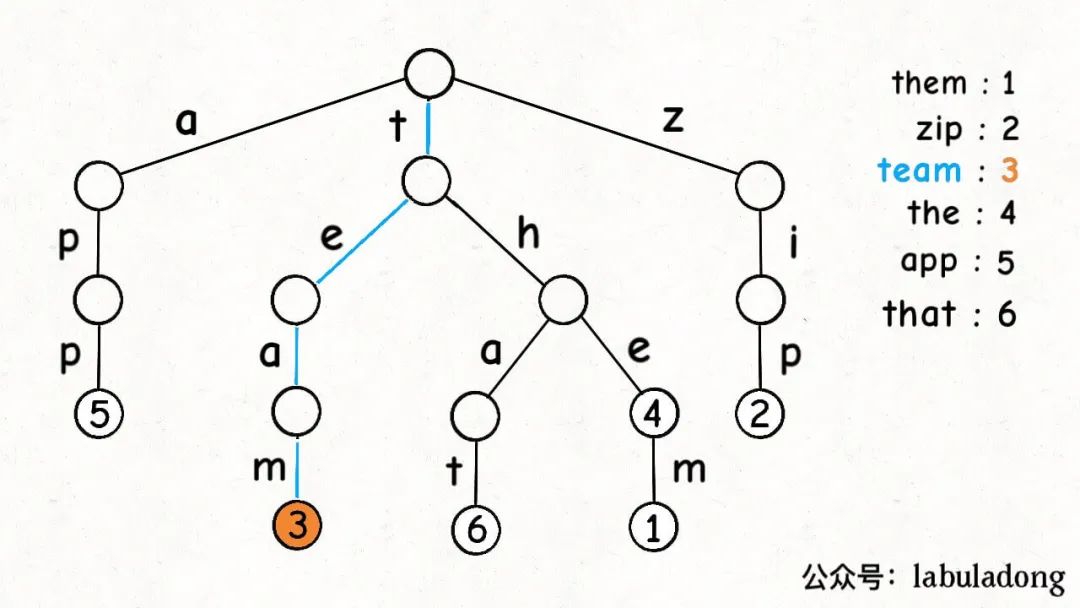
这是在 TrieMap<Integer> 中插入一些键值对后的样子，白色节点代表 val 字段为空，橙色节点代表 val 字段非空。

TrieNode 节点本身只存储 val 字段，并没有一个字段来存储字符，字符通过哈希表的 key 来确定。

形象理解就是，Trie 树用「树枝」存储字符串（键），用「节点」存储字符串（键）对应的数据（值）。

树枝与节点

Trie 树叫前缀树的原因是，因为其中的字符串共享前缀，相同前缀的字符串集中在 Trie 树中的一个子树上，给字符串的处理带来很大的便利。

TrieMap/TrieSet API 及实现

TrieMap

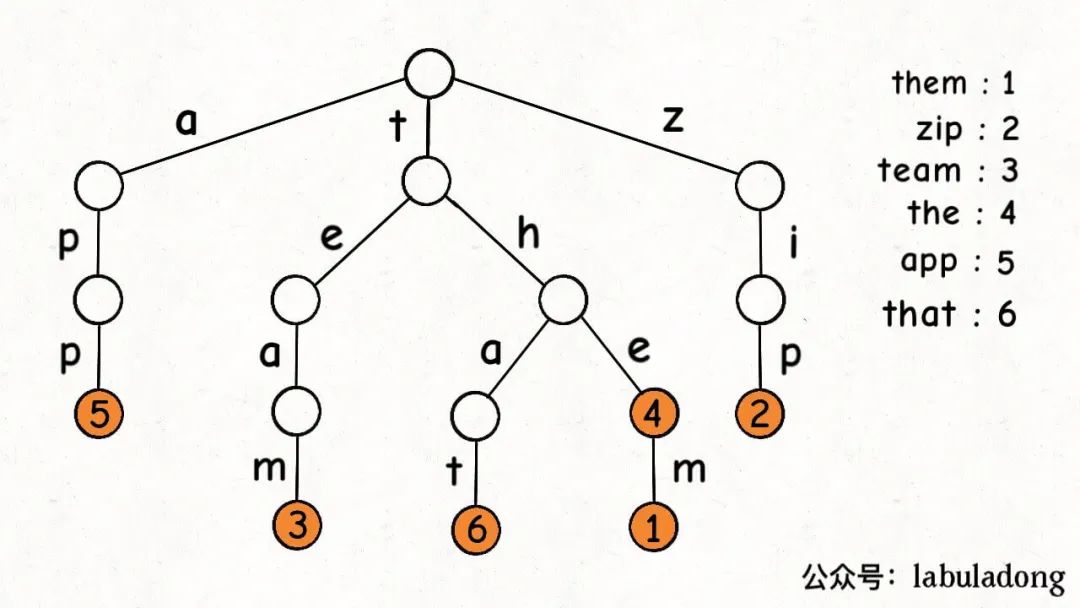
假设 TrieMap 中已经存储了如下键值对：

TrieMap 已经存储的键值对

TrieMap API

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
class TrieMap<V> {
    /***** 增、改 ******/

    // 在 Map 中添加 key
    public void put(String key, V val) {
    }

    /***** 删 *****/

    // 删除键 key 以及对应的值
    public void remove(String key) {
    }

    /***** 查 *****/

    // 搜索 key 对应的值，不存在则返回 null
    // get("the") -> 4
    // get("tha") -> null
    public V get(String key);

    // 判断 key 是否存在在 Map 中
    // containsKey("tea") -> false
    // containsKey("team") -> true
    public boolean containsKey(String key);

    // 在 Map 的所有键中搜索 query 的最短前缀
    // shortestPrefixOf("themxyz") -> "the"
    public String shortestPrefixOf(String query);

    // 在 Map 的所有键中搜索 query 的最长前缀
    // longestPrefixOf("themxyz") -> "them"
    public String longestPrefixOf(String query);

    // 搜索所有前缀为 prefix 的键
    // keysWithPrefix("th") -> ["that", "the", "them"]
    public List<String> keysWithPrefix(String prefix);

    // 判断是否存在前缀为 prefix 的键
    // hasKeyWithPrefix("tha") -> true
    // hasKeyWithPrefix("apple") -> false
    public boolean hasKeyWithPrefix(String prefix);

    // 通配符 . 匹配任意字符，搜索所有匹配的键
    // keysWithPattern("t.a.") -> ["team", "that"]
    public List<String> keysWithPattern(String pattern);

    // 通配符 . 匹配任意字符，判断是否存在匹配的键
    // hasKeyWithPattern(".ip") -> true
    // hasKeyWithPattern(".i") -> false
    public boolean hasKeyWithPattern(String pattern);

    // 返回 Map 中键值对的数量
    public int size();
    
    // 查询 TrieMap 中指定 key 出现的次数
    public int countWordsEqualTo(String key);
    
    //  查询 TrieMap 中以 prefix 为前缀的 key 的个数
    public int countWordsStartingWith(String prefix);
}

TrieSet 的 API 与 TrieMap API 几乎一致。

实现上述 API 函数

TrieNode、size、root 根节点

TrieMap 类中一定需要记录 Trie 的根节点 root，以及 Trie 树中的所有节点数量用于实现 size() 方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class TrieMap<V> {
    
    // 当前存在 Map 中的键值对个数
    private int size = 0;

    private static class TrieNode<V> {
        V val = null;
        int pass;
        int end;
        HashMap<Character, TrieNode<V>> children;
        
        public TrieNode() {
            val = null;
            pass = 0;
            end = 0;
            children = new HashMap<>();
        }
    }

    // Trie 树的根节点
    private TrieNode<V> root = null;
    
    public TrieMap() {
        root = new TrieNode();
    }

    // ...
    // 其他 API 实现
    // ...

    // 返回 Map 中键值对的个数
    public int size() {
        return size;
    }
}
工具函数 getNode

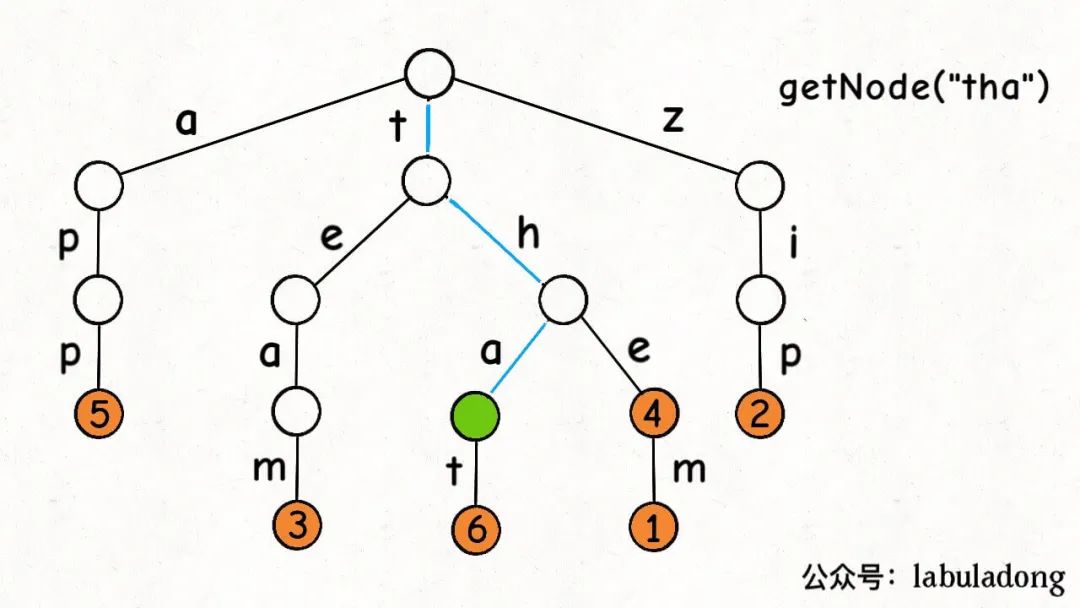
实现一个工具函数 getNode

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 从 node 节点搜索 key，如果存在返回「对应节点」，否则返回 null
private TrieNode<V> getNode(TrieNode<V> node, String key) {
    TrieNode<V> p = node; // 从节点 node 开始搜索 key
    for (int i = 0; i < key.length(); i++) {
        // 方法 1：
//            char path = key.charAt(i); // 确定路径
//            if (!p.children.containsKey(path)){ // 路径下方节点不存在
//                // 无法向下搜索
//                return null;
//            }
//            p = p.children.get(path);// 向下搜索
        // 方法 2：
        if (p == null) {
            return null; // 无法向下搜索
        }
        char path = key.charAt(i); // 确定路径
        p = p.children.get(path);// 向下搜索
    }
    return p;
}

getNode

containsKey 和 get

有了这个 getNode 函数，就能实现 containsKey 方法和 get 方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 搜索 key 对应的值，不存在则返回 null
public V get(String key) {
    // 从 root 开始搜索 key
    TrieNode<V> x = getNode(root, key);
    if (x == null || x.val == null) {
        // x 为空或 x 的 val 字段为空都说明 key 没有对应的值
        return null;
    }
    return x.val;
}

// 判断 key 是否存在在 Map 中
public boolean containsKey(String key) {
    return get(key) != null;
}

注意：就算 getNode(key) 的返回值 x 非空，也只能说明字符串 key 是一个「前缀」；除非 x.val 同时非空，才能判断键 key 存在。

hasKeyWithPrefix

但是，这个特性恰好能够帮我们实现 hasKeyWithPrefix 方法：

1
2
3
4
5
// 判断是和否存在前缀为 prefix 的键
public boolean hasKeyWithPrefix(String prefix) {
    // 只要能找到 prefix 对应的节点，就是存在前缀
    return getNode(root, prefix) != null;
}
shortestPrefixOf

类似 getNode 方法的逻辑，我们可以实现 shortestPrefixOf 方法，只要在第一次遇到存有 val 的节点的时候返回即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 在 Map 的所有键中搜索 query 的最短前缀
// shortestPrefixOf("themxyz") -> "the"
public String shortestPrefixOf(String query) {
    TrieNode<V> p = root;
    for (int i = 0; i < query.length(); i++) {
        if (p == null) { // 无法向下搜索
            return "";
        }
        if (p.val != null) { // 找到一个键是 query 的前缀
            return query.substring(0, i);
        }
        char path = query.charAt(i);
        p = p.children.get(path);
    }
    if (p != null && p.val != null) { // 如果 query 本身就是一个键
        return query;
    }
    return "";
}

注意，for 循环结束之后需要额外检查一下。因为 Trie 树中 「树枝」存储字符串，「节点」存储字符串对应的值，for 循环相当于只遍历了「树枝」，但漏掉了最后一个「节点」，即 query 本身就是 TrieMap 中的一个键的情况。

longestPrefixOf

类似地，可以实现 longestPrefixOf 方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 在 Map 的所有键中搜索 query 的最长前缀
// longestPrefixOf("themxyz") -> "them"
public String longestPrefixOf(String query) {
    int maxLen = 0; // 记录前缀的最大长度
    TrieNode<V> p = root;
    for (int i = 0; i < query.length(); i++) {
        if (p == null) {
            break; // 无法向下搜索
        }
        if (p.val != null) {
            maxLen = i; // 找到一个键是 query 的前缀，更新前缀的最大长度
        }
        // 向下搜索
        char path = query.charAt(i); 
        p = p.children.get(path);
    }
    if (p != null && p.val != null) {
        return query; // 如果 query 本身就是一个键，那么这就是最长前缀
    }
    return query.substring(0, maxLen);
}

每次遇到 p.val 非空的时候说明找到一个键，但是不要急着返回，而是更新 maxLen 变量，记录最长前缀的长度。

同样的，在 for 循环结束时要特殊判断一下，处理 query 本身就是键的情况。

keysWithPrefix

keysWithPrefix 方法，用于得到所有前缀为 prefix 的键。

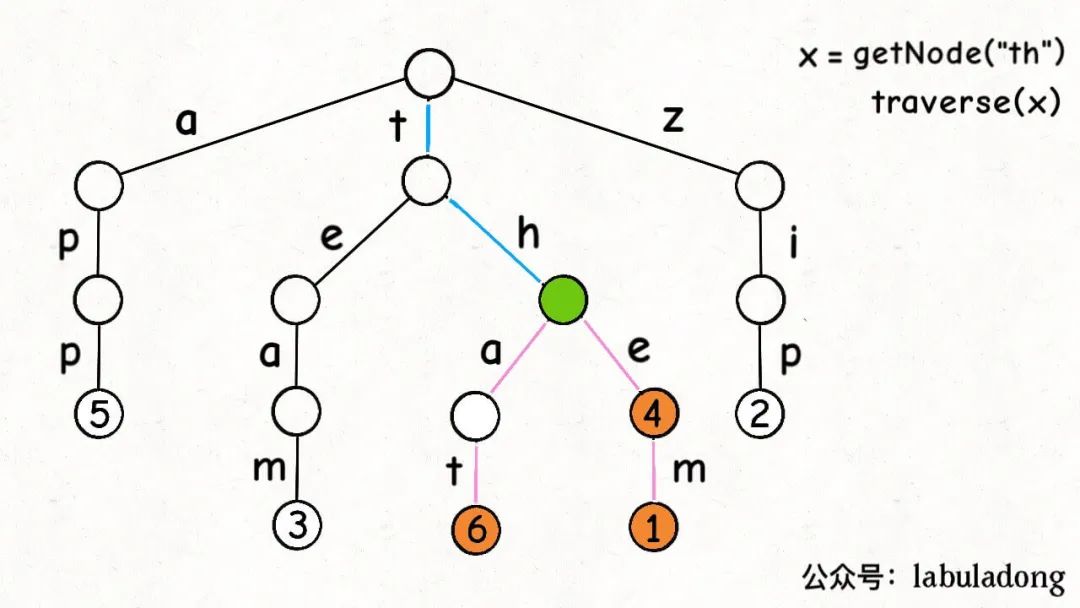
具体的方法是，先利用 getNode 函数在 Trie 树中找到 prefix 对应的节点 p，然后使用多叉树的遍历算法，遍历以 p 为根的这棵 Trie 树，找到所有键值对。

keysWithPrefix 实现流程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
// 搜索所有前缀为 prefix 的键
// keysWithPrefix("th") -> ["that", "the", "them"]
public List<String> keysWithPrefix(String prefix) {
    List<String> res = new LinkedList<>();
    // 找到匹配 prefix 在 Trie 树中的那个节点
    TrieNode<V> p = getNode(root, prefix);
    if (p == null) // 不存在 prefix
        return res;
    // 回溯遍历以 x 为根的这棵 Trie 树
    traverse(p, new StringBuffer(prefix), res);
    return res;
}

// 遍历以 node 节点为根的 Trie 树，找到所有「键」
private void traverse(TrieNode<V> node, StringBuffer path, List<String> res) {
    if (node == null) {
        // 到达 Trie 树底部叶子节点
        return;
    }
    if (node.val != null) {
        // 找到一个 key，添加到结果列表中
        res.add(path.toString());
    }
    // 回溯算法遍历框架
    // c 选择，node.children.keySet() 选择列表
    for (char c : node.children.keySet()) {
        // 做选择
        path.append(c);
        traverse(node.children.get(c), path, res);
        // 撤销选择
        path.deleteCharAt(path.length() - 1);
    }
}

traverse 函数使用的是回溯算法框架，其核心就是 for 循环里的递归，在递归调用前「做选择」，在递归后「撤销选择」。

回溯算法与 DFS 算法非常类似，两者的差别是：回溯算法是在遍历「树枝」，DFS 算法是在遍历「节点」。由于 Trie 树将字符存储在 「树枝」上，traverse 函数是在遍历树枝上的字符，所以采用的是回溯算法框架。

keysWithPattern

keysWithPattern 方法，使用通配符来匹配多个键，其关键就在于通配符.可以匹配字符。

在代码实现上，用 path 变量记录匹配键的路径，遇到通配符时使用类似回溯算法的框架就行了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
// 通配符 . 匹配任意字符，搜索所有匹配的键
// keysWithPattern("t.a.") -> ["team", "that"]
public List<String> keysWithPattern(String pattern) {
    List<String> res = new LinkedList<>();
    traverse(root, new StringBuilder(), pattern, 0, res);
    return res;
}

// 遍历函数，尝试在「以 node 为根的 Trie 树中」匹配 pattern[i..]
private void traverse(TrieNode<V> node, StringBuilder path, String pattern, int i, List<String> res) {
    if (node == null) {
        // 树枝不存在，即匹配失败
        return;
    }
    if (i == pattern.length()) {
        // pattern 匹配完成
        if (node.val != null) {
            // 如果这个节点存储着 val，则找到一个匹配的键
            res.add(path.toString());
        }
        return;
    }
    char c = pattern.charAt(i);
    if (c == '.') {
        // pattern[i] 是通配符，可以变化成任意字符
        // 多叉树（回溯算法）遍历框架
        for (char j : node.children.keySet()) {
            path.append(j); // 做选择
            traverse(node.children.get(j), path, pattern, i + 1, res);
            path.deleteCharAt(path.length() - 1); // 撤销选择
        }
    } else {
        // pattern[i] 是普通字符 c
        path.append(c); // 做选择
        traverse(node.children.get(c), path, pattern, i + 1, res);
        path.deleteCharAt(path.length() - 1); // 撤销选择
    }
}

使用 GIF 描述匹配 "t.a." 的过程：

匹配 "t.a." 的过程

可以看到，keysWithPattern 和 keysWithPrefix 的实现是有些类似的。

如果使用 children 是使用数组存储的，那么它们返回的结果列表一定是符合「字典序」的。

因为每一个节点的 children 数组都是从左到右进行遍历，即按照 ASCII 码从小到大的顺序递归遍历，得到的结果自然是符合字典序的。

hasKeyWithPattern

hasKeyWithPattern 判断是否存在匹配的键。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 通配符 . 匹配任意字符，判断是否存在匹配的键
// hasKeyWithPattern(".ip") -> true
// hasKeyWithPattern(".i") -> false
public boolean hasKeyWithPattern(String pattern) {
    // 从 root 节点开始匹配 pattern[0..]
    return traverse(root, pattern, 0);
}

// 从 node 节点开始匹配 pattern[i..]，返回是否成功匹配
private boolean traverse(TrieNode<V> node, String pattern, int i) {
    if (node == null) {
        // 树枝不存在，即匹配失败
        return false;
    }
    if (i == pattern.length()) {
        // 模式串走到头了，看看匹配到的是否是一个键
        return node.val != null;
    }
    char c = pattern.charAt(i);
    // 没有遇到通配符
    if (c != '.') {
        // 从 node.children.get(c) 节点开始匹配 pattern[i+1..]
        return traverse(node.children.get(c), pattern, i + 1);
    }
    // 遇到通配符
    for (char j : node.children.keySet()) {
        // pattern[j] 可以变化成任意字符，尝试所有可能，只要遇到一个匹配成功就返回
        if (traverse(node.children.get(j), pattern, i + 1)) {
            return true;
        }
    }
    // 都没有匹配
    return false;
}

到此，TrieMap 的所有和前缀相关的方法都实现完了。

现在还需要实现 put 和 remove 以及 countWordsEqualTo 和 countWordsStartingWith 方法。

put

put 方法向 map 中添加或修改键值对。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 向 map 中添加或修改键值对
public void put(String key, V val) {
    if (key == null) {
        return;
    }
    if (!containsKey(key)) {
        size++;
    }
    TrieNode<V> node = root; // 从根节点开始
    node.pass++; // 根节点 pass++
    for (int i = 0; i < key.length(); i++) { // 遍历字符串
        char path = key.charAt(i); // 确定字符路径
        if (!node.children.containsKey(path)) { // 如果路径下方节点不存在
            node.children.put(path, new TrieNode<>()); // 新建节点
        }
        node = node.children.get(path); // 节点存在，node 向下移动
        node.pass++; // 经过的节点 pass++
    }
    // key 的路径已插入完成，将值 val 存入节点
    node.val = val;
    node.end++; // 最后的节点 end++
}

Trie 树中的 key 就是「树枝」，值就是「节点」，所以插入的逻辑就是沿路新建「树枝」，把 key 的整条「树枝」构建出来后，在树枝末端的「节点」中存储 val。

put 方法

remove

remove 方法在 map 中删除 key。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 在 map 中删除 key
public void remove(String key) {
    if (key == null) {
        return;
    }
    if (!containsKey(key)) { // 判断 key 是否在 Trie 树中
        return;
    }
    size--; // 键值对数量 - 1
    TrieNode<V> node = root; // 从根节点开始
    node.pass--; // 根节点 pass - 1
    for (int i = 0; i < key.length(); i++) {
        char path = key.charAt(i); // 确定字符路径
        if (--node.children.get(path).pass == 0) { // 如果路径下面的节点 pass - 1 == 0
            node.children.remove(path); // 移除该节点，后续节点会被 gc 掉
            return; // 直接返回
        }
        node = node.children.get(path); // node 向下移动
    }
    node.end--; // 最终节点 end - 1
}

如果想删除键 team，那么需要删除 eam 这条树枝，才符合逻辑。

remove 方法

删多了不行，删少了也不行，否则前面实现的 hasKeyWithPrefix 就会出错。

如何判断一个节点是否需要被删除呢？节点的 pass 值为 0 的时候，就需要被移除，后续的节点会被 GC 掉。

countWordsEqualTo

countWordsEqualTo 查询 TrieMap 中指定 key 出现的次数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 查询 TrieMap 中指定 key 出现的次数
public int countWordsEqualTo(String key) {
    if (key == null) {
        return 0;
    }
    if (!containsKey(key)) {
        return 0;
    }
    TrieNode<V> node = root; // 从根节点开始
    for (int i = 0; i < key.length(); i++) { // 遍历字符串
        char path = key.charAt(i); // 确定字符路径
        if (!node.children.containsKey(path)) { // 如果路径下方不存在节点，返回 0
            return 0;
        }
        node = node.children.get(path); // 节点存在，向下移动
    }
    return node.end; // 返回 end 值
}
countWordsStartingWith
1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 查询 TrieMap 中以 prefix 为前缀的 key 的个数
public int countWordsStartingWith(String prefix) {
    if (prefix == null)
        return 0;
    TrieNode<V> node = root;
    for (int i = 0; i < prefix.length(); i++) {
        char path = prefix.charAt(i);
        if (!node.children.containsKey(path)) {
            return 0;
        }
        node = node.children.get(path);
    }
    return node.pass; // 返回 pass 值
}

countWordsStartingWith 方法与 countWordsEqualTo 方法的主要不同在于，抵达最终节点时，一个返回 end 值，一个返回 pass 值。

到这里，TrieMap 的所有 API 就都实现完毕了。

TrieSet

只要对 TrieMap 做简单的封装，就可以实现 TrieSet。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class TrieSet<V> {
    // 底层用一个 TrieMap，键就是 TrieSet，值仅仅起到占位的作用
    // 值的类型可以随便设置，参考 Java 标准库设置为 Object
    private final TrieMap<Object> map = new TrieMap<>();

    public void add(String key) {
        map.put(key, new Object());
    }

    public void remove(String key) {
        map.remove(key);
    }

    public boolean contains(String key) {
        return map.containsKey(key);
    }

    public String shortestPrefixOf(String query) {
        return map.shortestPrefixOf(query);
    }

    public String longestPrefixOf(String query) {
        return map.longestPrefixOf(query);
    }

    public List<String> keysWithPrefix(String prefix) {
        return map.keysWithPrefix(prefix);
    }

    public boolean hasKeyWithPrefix(String prefix) {
        return map.hasKeyWithPrefix(prefix);
    }

    public List<String> keysWithPattern(String pattern) {
        return map.keysWithPattern(pattern);
    }

    public boolean hasKeyWithPattern(String pattern) {
        return map.hasKeyWithPattern(pattern);
    }

    public int size() {
        return map.size();
    }

    public int countWordEqualTo(String key) {
        return map.countWordsEqualTo(key);
    }

    public int countWordsStartingWith(String prefix) {
        return map.countWordsStartingWith(prefix);
    }
}

秒杀题目

牛客-NC124-字典树的实现

牛客-NC124-字典树的实现

只需要使用 TrieMap 中的部分 API 封装一个 Trie 类即可解决该题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
import java.util.*;


public class Solution {
    /**
     *
     * @param operators string字符串二维数组 the ops
     * @return string字符串一维数组
     */
    public String[] trieU (String[][] operators) {
        // write code here
        List<String> ans = new ArrayList<>();
        Trie trie = new Trie();
        for (String[] opera : operators) {
            if (opera[0].equals("1")) {
                trie.insert(opera[1]);
            } else if (opera[0].equals("2")) {
                trie.delete(opera[1]);
            } else if (opera[0].equals("3")) {
                ans.add(trie.search(opera[1]) ? "YES" : "NO");
            } else if (opera[0].equals("4")) {
                ans.add(String.valueOf(trie.prefixNumber(opera[1])));
            }
        }
        return ans.toArray(new String[0]);
    }
}

class Trie {
    private final TrieMap<Object> trieMap = new TrieMap<>();

    public void insert(String word) {
        trieMap.put(word, new Object());
    }
    
    public void delete(String word) {
        trieMap.remove(word);
    }

    public boolean search(String word) {
        return trieMap.containsKey(word);
    }

    public int prefixNumber(String pre) {
        return trieMap.countWordsStartingWith(pre);
    }
}

class TrieMap<V> {
    private static class TrieNode<V> {
        private V val;
        private int pass;
        private int end;
        private HashMap<Character, TrieNode<V>> children;
        public TrieNode() {
            val = null;
            pass = 0;
            end = 0;
            children = new HashMap<>();
        }
    }
    
    private int size = 0;
    
    private TrieNode<V> root = null;

    public TrieMap() {
        root = new TrieNode<>();
    }

    private TrieNode<V> getNode(String key, TrieNode<V> node) {
        if (key == null) {
            return null;
        }
        TrieNode<V> p = node;
        for (int i = 0; i < key.length(); i++) {
            if (p == null) {
                return null;
            }
            char path = key.charAt(i);
            p = p.children.get(path);
        }
        return p;
    }

    public V get(String key) {
        if (key == null) {
            return null;
        }
        TrieNode<V> p = getNode(key, root);
        if (p == null || p.val == null) {
            return null;
        }
        return p.val;
    }

    public boolean containsKey(String key) {
        return get(key) != null;
    }

    public void put(String key, V val) {
        if (key == null) {
            return;
        }
        if (!containsKey(key)) {
            size++;
        }
        TrieNode<V> node = root;
        node.pass++;
        for (int i = 0; i < key.length(); i++) {
            char path = key.charAt(i);
            if (!node.children.containsKey(path)) {
                node.children.put(path, new TrieNode<>());
            }
            node = node.children.get(path);
            node.pass++;
        }
        node.val = val;
        node.end++;
    }

    public void remove(String key) {
        if (key == null) {
            return;
        }
        if (!containsKey(key)) {
            return;
        }
        size--;
        TrieNode<V> node = root;
        node.pass--;
        for (int i = 0; i < key.length(); i++) {
            char path = key.charAt(i);
            if (--node.children.get(path).pass == 0) {
                node.children.remove(path);
                return;
            }
            node = node.children.get(path);
        }
        node.end--;
    }

    public int countWordsStartingWith(String prefix) {
        if (prefix == null) {
            return 0;
        }
        TrieNode<V> node = root;
        for (int i = 0; i < prefix.length(); i++) {
            char path = prefix.charAt(i);
            if(!node.children.containsKey(path)) {
                return 0;
            }
            node = node.children.get(path);
        }
        return node.pass;
    }

    public int size() {
        return size;
    }
}

力扣-208-实现 Trie（前缀树）

力扣-208-实现 Trie（前缀树）

只需要使用 TrieMap 中的部分 API 封装一个 Trie 类即可解决该题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
class Trie {
    private final TrieMap<Object> map;
    public Trie() {
        map = new TrieMap<>();
    }
    
    public void insert(String word) {
        map.put(word, new Object());
    }
    
    public boolean search(String word) {
        return map.containsKey(word);
    }
    
    public boolean startsWith(String prefix) {
        return map.hasKeyWithPrefix(prefix);
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

class TrieMap<V> {
    private static class TrieNode<V> {
        int pass;
        int end;
        V val;
        HashMap<Character, TrieNode<V>> children;

        public TrieNode() {
            pass = 0;
            end = 0;
            val = null;
            children = new HashMap<>();
        }
    }

    private int size = 0;

    private TrieNode<V> root = null;

    public TrieMap() {
        root = new TrieNode<>();
    }

    public TrieNode<V> getNode(TrieNode<V> node, String key) {
        if (key == null) {
            return null;
        }
        TrieNode<V> p = node;
        for (int i = 0; i < key.length(); i++) {
            if (p == null) {
                return null;
            }
            char path = key.charAt(i);
            p = p.children.get(path);
        }
        return p;
    }

    public V get(String key) {
        if (key == null) {
            return null;
        }
        TrieNode<V> p = getNode(root, key);
        if (p == null || p.val == null) {
            return null;
        }
        return p.val;
    }

    public boolean containsKey(String key) {
    return get(key) != null;
    }
        

    // 修改或更新
    public void put(String key, V val) {
        if (key == null) {
            return;
        }
        if (!containsKey(key)) {
            size++;
        }
        TrieNode<V> node = root;
        node.pass++;
        for (int i = 0; i < key.length(); i++) {
            char path = key.charAt(i);
            if (!node.children.containsKey(path)) {
                node.children.put(path, new TrieNode<>());
            }
            node = node.children.get(path);
            node.pass++;
        }
        node.val = val;
        node.end++;
    }

    public boolean hasKeyWithPrefix(String prefix) {
        return getNode(root, prefix) != null;
    }
}

力扣-211-添加与搜索单词-数据结构设计

力扣-211-添加与搜索单词

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
class WordDictionary {
    private final TrieMap<Object> map;
    public WordDictionary() {
        map = new TrieMap<>();
    }
    
    public void addWord(String word) {
        map.put(word, new Object());
    }
    
    public boolean search(String word) {
        return map.hasKeyWithPattern(word);
    }
}

/**
 * Your WordDictionary object will be instantiated and called as such:
 * WordDictionary obj = new WordDictionary();
 * obj.addWord(word);
 * boolean param_2 = obj.search(word);
 */

class TrieMap<V> {
    private static class TrieNode<V> {
        int pass;
        int end;
        V val;
        HashMap<Character, TrieNode<V>> children;

        public TrieNode() {
            pass = 0;
            end = 0;
            val = null;
            children = new HashMap<>();
        }
    }

    private int size = 0;
    private TrieNode<V> root = null;
    public TrieMap() {
        root = new TrieNode();
    }

    private TrieNode<V> getNode(TrieNode<V> node, String key) {
        if (key == null) {
            return null;
        }
        TrieNode<V> p = node;
        for (int i = 0; i < key.length(); i++) {
            if (p == null) {
                return null;
            }
            char path = key.charAt(i);
            p = p.children.get(path);
        }
        return p;
    }

    public V get(String key) {
        if (key == null) {
            return null;
        }
        TrieNode<V> p = getNode(root, key);
        if (p == null || p.val == null) {
            return null;
        }
        return p.val;
    }

    public boolean containsKey(String key) {
        return get(key) != null;
    } 

    public void put(String key, V val) {
        if (key == null) {
            return;
        }
        if (!containsKey(key)) {
            size++;
        }
        TrieNode<V> node = root;
        node.pass++;
        for (int i = 0; i < key.length(); i++) {
            char path = key.charAt(i);
            if (!node.children.containsKey(path)) {
                node.children.put(path, new TrieNode<>());
            }
            node = node.children.get(path);
            node.pass++;
        }
        node.val = val;
        node.end++;
    }

    public boolean hasKeyWithPattern(String pattern) {
        if (pattern == null) {
            return false;
        }
        return traverse(root, pattern, 0);    
    }

    private boolean traverse(TrieNode<V> node, String pattern, int i) {
        if (node == null) {
            return false;
        }
        if (i == pattern.length()) {
            return node.val != null;
        }
        char path = pattern.charAt(i);
        if (path != '.') {
            return traverse(node.children.get(path), pattern, i + 1);
        }
        for (char c : node.children.keySet()) {
            if (traverse(node.children.get(c), pattern, i + 1)) {
                return true;
            }
        }
        return false;
    }

}

力扣-677-键值映射

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
class MapSum {
    private TrieMap<Integer> map = null;
    public MapSum() {
        map = new TrieMap<>();
    }
    
    public void insert(String key, int val) {
        map.put(key, val);
    }
    
    public int sum(String prefix) {
        List<String> keys = map.keysWithPrefix(prefix);
        int res = 0;
        for (String key : keys) {
            res += map.get(key);
        }
        return res;
    }
}

/**
 * Your MapSum object will be instantiated and called as such:
 * MapSum obj = new MapSum();
 * obj.insert(key,val);
 * int param_2 = obj.sum(prefix);
 */

class TrieMap<V> {
    private static class TrieNode<V> {
        int pass;
        int end;
        V val;
        HashMap<Character, TrieNode<V>> children;

        public TrieNode() {
            pass = 0;
            end = 0;
            val = null;
            children = new HashMap<>();
        }
    }

    private int size = 0;
    private TrieNode<V> root = null;
    public TrieMap() {
        root = new TrieNode();
    }

    private TrieNode<V> getNode(TrieNode<V> node, String key) {
        if (key == null) {
            return null;
        }
        TrieNode<V> p = node;
        for (int i = 0; i < key.length(); i++) {
            if (p == null) {
                return null;
            }
            char path = key.charAt(i);
            p = p.children.get(path);
        }
        return p;
    }

    public V get(String key) {
        if (key == null) {
            return null;
        }
        TrieNode<V> p = getNode(root, key);
        if (p == null || p.val == null) {
            return null;
        }
        return p.val;
    }

    public boolean containsKey(String key) {
        return get(key) != null;
    }

    public void put(String key, V val) {
        if (key == null) {
            return;
        }
        TrieNode<V> node = root;
        node.pass++;
        for (int i = 0; i < key.length(); i++) {
            char path = key.charAt(i);
            if (!node.children.containsKey(path)) {
                node.children.put(path, new TrieNode());
            }
            node = node.children.get(path);
            node.pass++;
        }
        node.val = val;
        node.end++;
    }

    public List<String> keysWithPrefix(String prefix) {
        List<String> res = new LinkedList<>();
        TrieNode<V> p = getNode(root, prefix);
        if (p == null) {
            return res;
        }
        traverse(p, new StringBuilder(prefix), res);
        return res;
    }

    public void traverse(TrieNode<V> node, StringBuilder path, List<String> res) {
        if (node == null) {
            return;
        }
        if (node.val != null) {
            res.add(path.toString());
        }
        for (char c : node.children.keySet()) {
            path.append(c);
            traverse(node.children.get(c), path, res);
            path.deleteCharAt(path.length() - 1);
        }
    }

}

参考资料

  1. 算法（第四版）
  2. labuladong 的算法小抄
  3. 程序员代码指南
  4. 牛客网
  5. 力扣网