本文使用双指针解决了如下算法问题:
力扣
141.环形链表
力扣
142.环形链表II
力扣
160.相交链表
力扣
19.删除链表的倒数第 N 个节点
力扣
21.合并两个有序链表
力扣
23.合并 K 个升序链表
力扣
86.分割链表
力扣
876.链表的中间节点
剑指
Offer 22.链表中倒数第 k 个节点
剑指
Offer 25.合并两个排序的链表
剑指
Offer 52.两个链表的第一个公共节点
剑指
OfferII 021.删除链表的倒数第 n 个节点
剑指
OfferII 022.链表中环的入口节点
剑指
OfferII 023.两个链表的第一个重合节点
剑指
OfferII 078.合并排序链表
描述
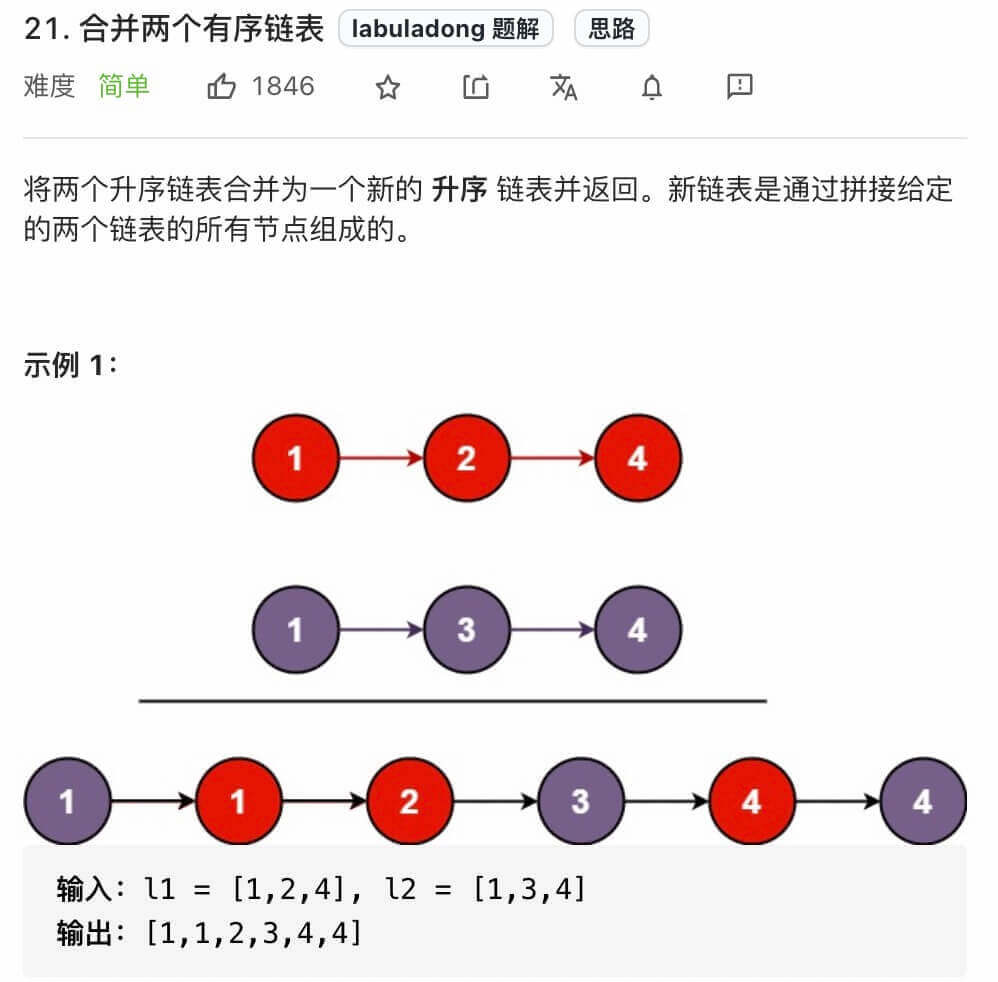
思路
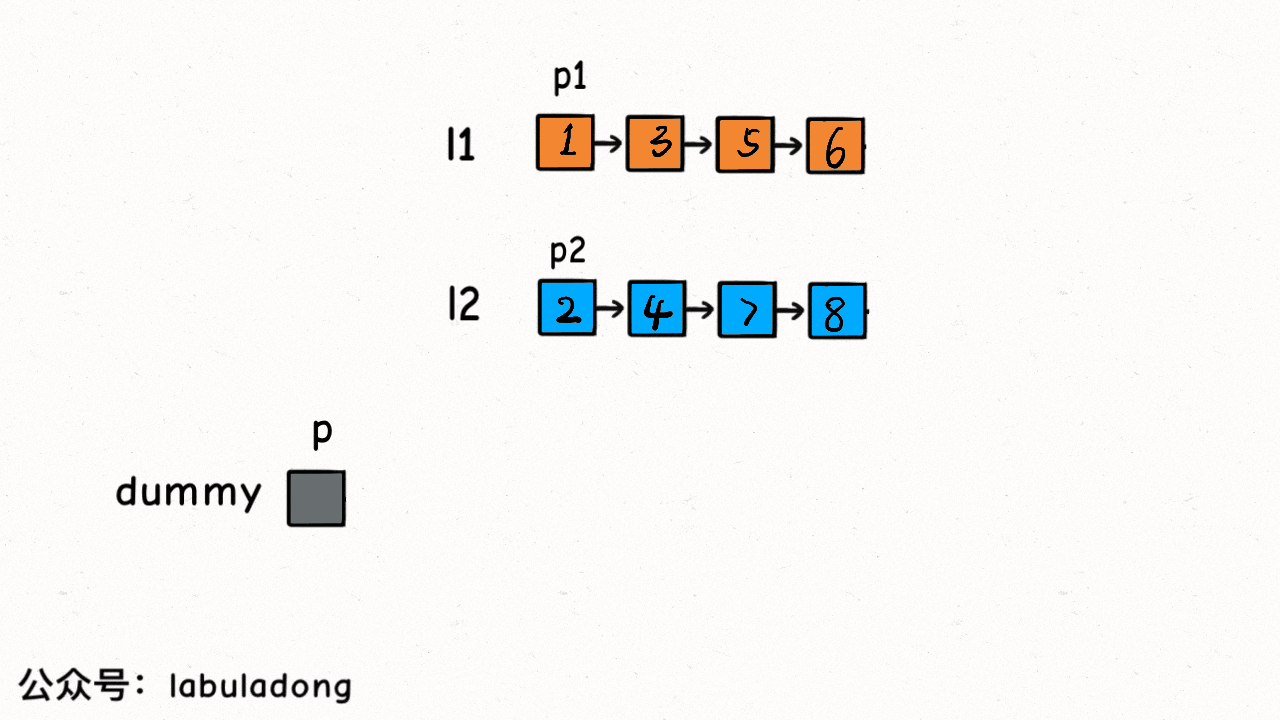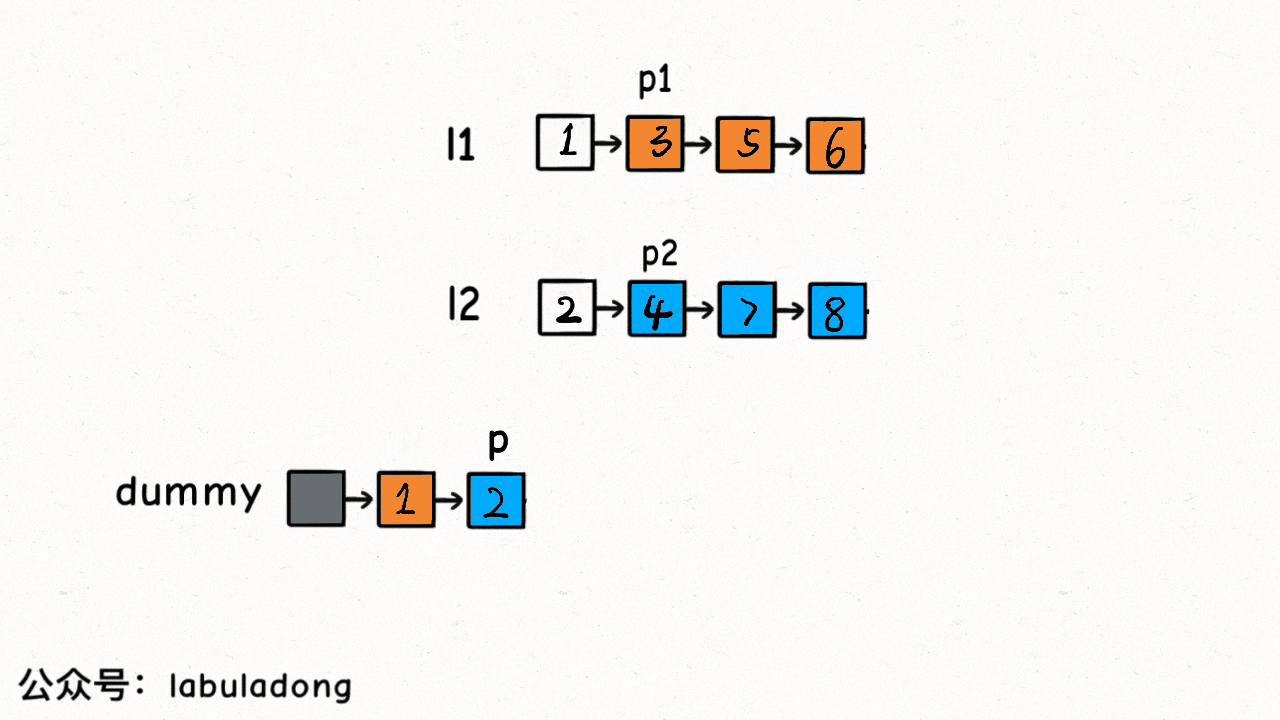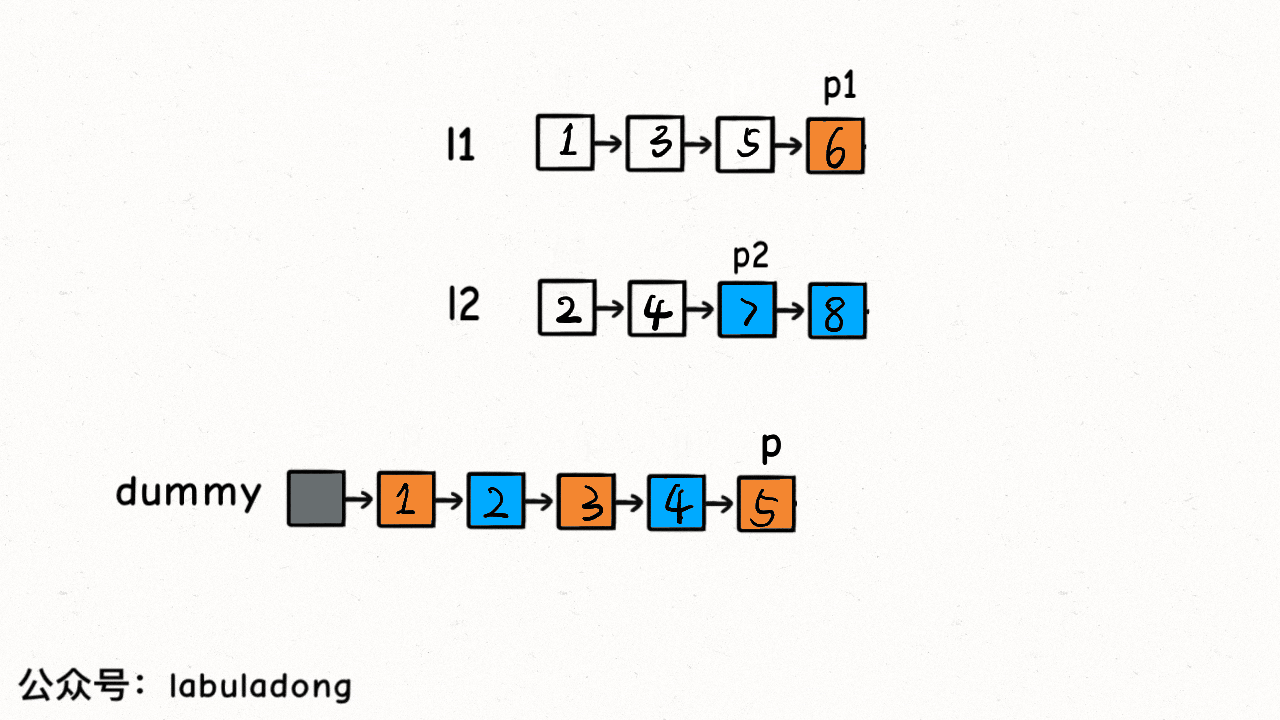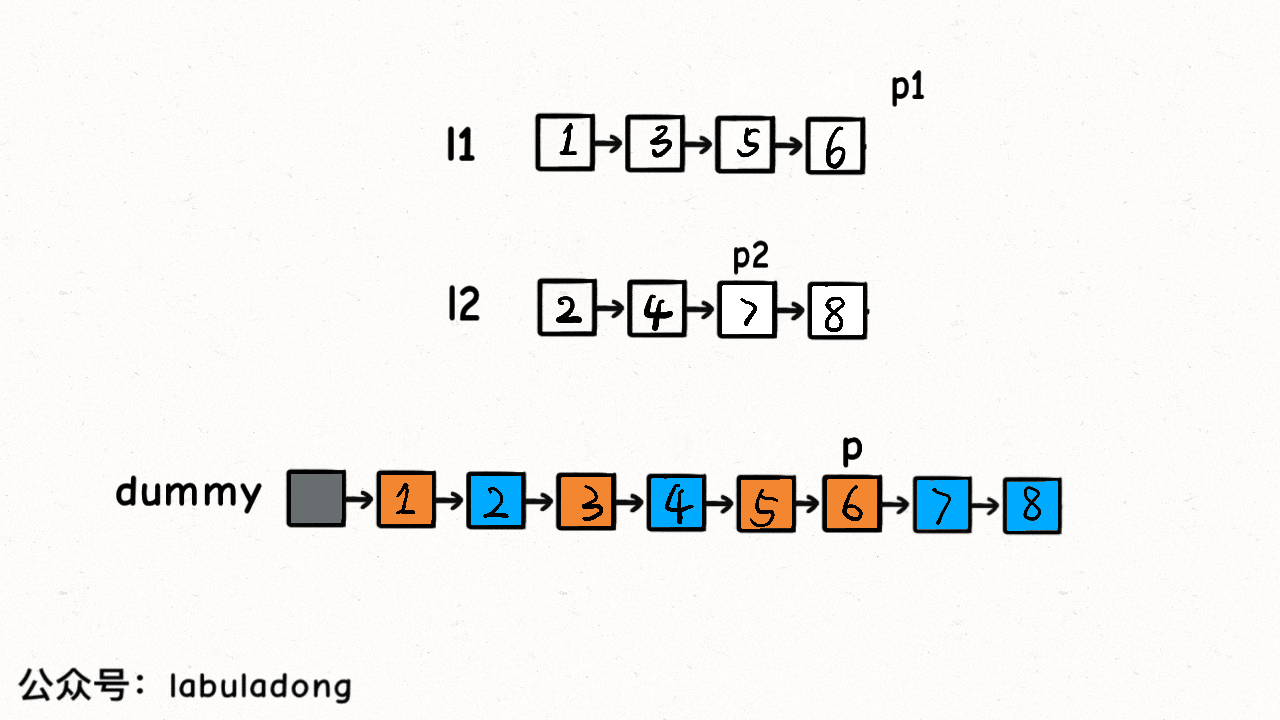
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| ListNode mergeTwoLists(ListNode list1, ListNode list2) {
if (list1 == null)
return list2;
if (list2 == null)
return list1;
ListNode dummy = new ListNode(-1);
ListNode p = dummy;
ListNode p1 = list1, p2 = list2;
while (p1 != null && p2 != null) {
if (p1.val < p2.val) {
p.next = p1;
p1 = p1.next;
} else {
p.next = p2;
p2 = p2.next;
}
p = p.next;
}
if (p1 != null) {
p.next = p1;
}
if (p2 != null) {
p.next = p2;
}
return dummy.next;
}
|
技巧:虚拟头节点
「虚拟头节点」,dummy 节点。如果不使用 dummy
虚拟节点,代码会复杂一些,需要额外处理指针 p 为空的情况。而有了 dummy
节点这个占位符,可以避免处理空指针的情况,降低代码的复杂性。
什么时候需要用虚拟头节点?
当需要创造一条新链表的时候,可以使用虚拟头节点简化边界情况的处理。
比如,把两条有序链表合并成一条新的有序链表,是创造一条新链表。把一条链表分解成两条链表,也是在创造新链表。这些情况都可以使用虚拟头节点简化边界情况的处理。
描述
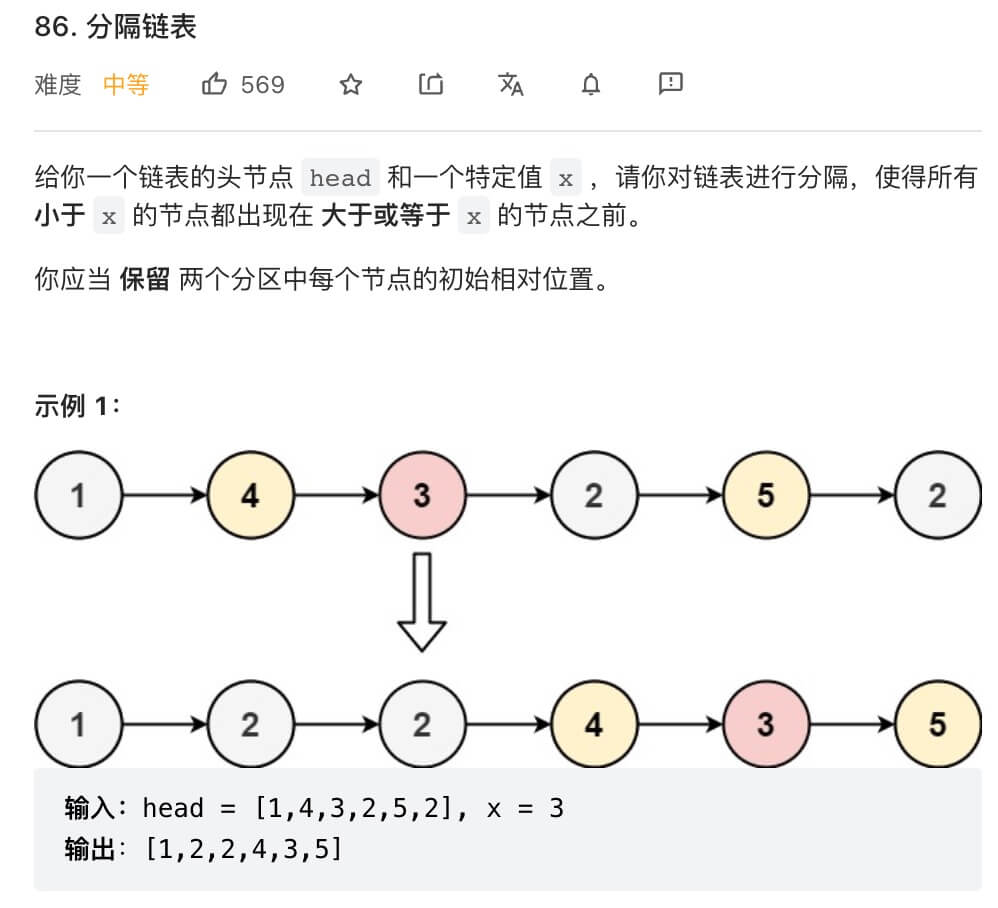
思路
在合并两个有序链表时,我们合二为一,而这道题需要我们将原链表一分为二。具体来说,我们可以把原链表分成两个小链表,一个链表中的元素大小都小于
x,另一个链表中的元素都大于等于
x,最后再把这两条链表接到一起,就得到了题目想要的结果。
代码
注意虚拟头节点的运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| ListNode partition(ListNode head, int x) {
ListNode dummy1 = new ListNode(-1);
ListNode dummy2 = new ListNode(-1);
ListNode p1 = dummy1, p2 = dummy2;
ListNode p = head;
while (p != null) {
if (p.val < x) {
p1.next = p;
p1 = p1.next;
} else {
p2.next = p;
p2 = p2.next;
}
ListNode temp = p.next;
p.next = null;
p = temp;
}
p1.next = dummy2.next;
return dummy1.next;
}
|
描述

思路
合并 k 个升序链表的逻辑类似合并两个链表,难点在于如何快速得到 k
个节点中的最小节点,接到结果链表上?
这里使用优先级队列(二叉堆),把链表节点放入一个最小堆,就可以每次获得
k 个节点中的最小节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| ListNode mergeKLists(ListNode[] lists) {
if (lists == null || lists.length == 0)
return null;
ListNode dummy = new ListNode(-1);
ListNode p = dummy;
PriorityQueue<ListNode> pq = new PriorityQueue<>(
lists.length, (a, b) -> (a.val - b.val));
for (ListNode head : lists) {
if (head != null)
pq.add(head);
}
while(!pq.isEmpty()) {
ListNode curNode = pq.poll();
p.next = curNode;
if (curNode.next != null)
pq.add(curNode.next);
p = p.next;
}
return dummy.next;
}
|
时间复杂度是多少呢?
优先级队列 pq 中的元素个数最多是 k,所以一次 poll 或者 add
方法的时间复杂度是 \(O(logk)\);所有的链表节点都会被加入和弹出
pq,所以算法整体的时间复杂度是 \(O(Nlogk)\),其中 k 是链表的条数,N
是这些链表的节点总数。
快指针先行 k 步
链表不能逆序遍历,那么如何寻找从后往前数的第 k 个节点呢?
可能有这样一种想法,假设链表有 n 个节点,倒数第 k 个节点就是正数第 n
- k + 1 个节点,直接遍历不就可以了吗?
但是,算法题一般只给 ListNode
头节点代表一条单链表,不能直接得出这条链表的长度
n,而需要先遍历一遍链表算出 n 的值,然后再遍历链表计算第 n - k + 1
个节点。
也就是说,这种解法需要遍历两次链表才能得出倒数第 k 个节点。
那么,如何只遍历一次链表,就算出倒数第 k
个节点?这也是面试官希望给出的解法。
假设 k = 2,思路如下:
首先,我们先让一个指针 p1 指向链表的头节点 head,然后走 k 步:
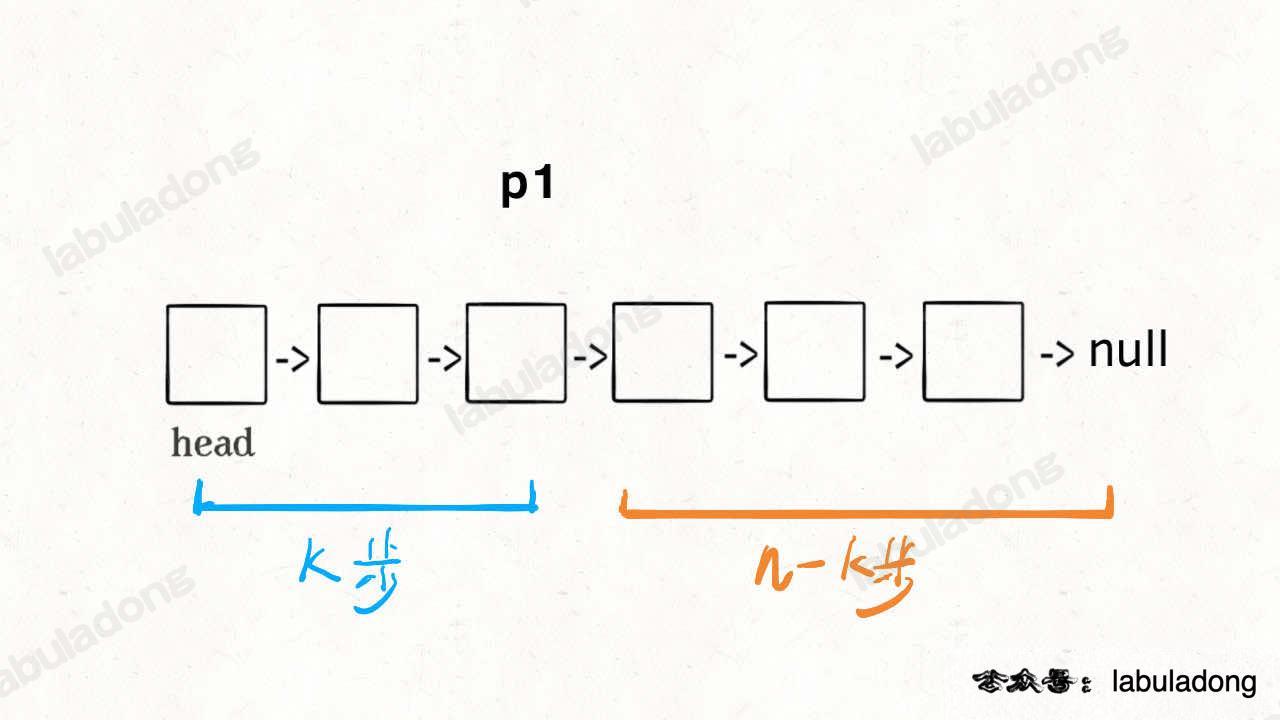
现在的 p1,只要再走 n - k 步,就能走到链表末尾的空指针。




