手撕算法必备技巧（叁）—— 双指针（数组篇）

发表于 2023-05-19 更新于 2023-05-21 分类于算法，双指针本文字数： 3k 阅读时长 ≈ 11 分钟阅读次数：

书接上篇手撕算法必备技巧（贰） —— 双指针（链表篇），前文提到了什么是双指针技巧，以及该技巧如何在链表中应用。本文主要讲解双指针技巧是如何解决大厂面试中常见的数组问题。

考察过该技巧的公司有阿里巴巴、腾讯、美团、拼多多、百度、华为等大厂。

食用指南： ⭐️为一刷必做题，便于快速理解双指针技巧；无星题目可在刷完⭐️题目后再做，用于拓展学习双指针技巧如何与其他算法知识结合使用。

日志更新：文章底部给出了更新日志，帮助小伙伴们快速知晓最近优化了哪些技巧，更新了哪些题目。

我相信，友好的讨论交流会让彼此快速进步！文章难免有疏漏之处，十分欢迎大家在评论区中批评指正。

前文已经阐述完了双指针技巧的使用，也给出了大量可以使用双指针技巧解决的链表题目。那么，接下来我们直接从题目入手，看看双指针技巧如何应用到数组题目上。

小提示，建议新同学要将题目的流程手绘一遍，这样更有助于理解！

快慢指针技巧

⭐️删除有序数组中的重复项（力扣26）

题目描述

思路（双指针）

首先，简单解释一下原地删除的概念：

原地删除就是不能新建一个数组，把去重后的元素放进新数组中，而是只能在原数组中去重。

题目中提到数组是一个升序数组，所以重复的元素一定连在一起。因为数组是一个连续的数据结构，如果找到一个重复元素，将其删除，然后还要把后面的元素迁移，这样时间复杂度非常高，为 \(O(n^2)\) 级别。

如果想要一遍扫描就完成原地去重，那么就可以使用双指针技巧中的「快慢指针」技巧啦。

初始化快慢指针，快指针 fast 向前遍历，当 fast 找到一个和 slow 不相同的元素时，slow 前进一步，并给 slow 处的元素更新为 fast 指向的元素值。如此，便保证了 nums[0...slow] 都是无重复的元素。

直到 fast 遍历完整个数组，nums[0...slow] 就是最终的去重结果。

参考代码

public int removeDuplicates(int[] nums) {
    // 数组为空，返回 0
    if (nums == null || nums.length == 0) {
        return 0;
    }
    // 初始化快慢指针
    int slow = 0, fast = 0;
    while (fast < nums.length) {
        // 如果 fast 指向的元素 != slow 指向的元素
        if (nums[fast] != nums[slow]) {
            // slow 前进一步
            slow++;
            // 更新 slow 的元素值
            nums[slow] = nums[fast];
            // 由此保证了 nums[0...slow] 都是去重后的元素
        }
        // 快指针前进一步
        fast++;
    }
    // nums[0...slow] 共有 slow + 1 个元素
    return slow + 1;
}

时间复杂度

\(O(n)\)

n 是数组元素的个数，只需遍历一次数组即可完成去重。

空间复杂度

\(O(1)\)

只有到了常数个变量。

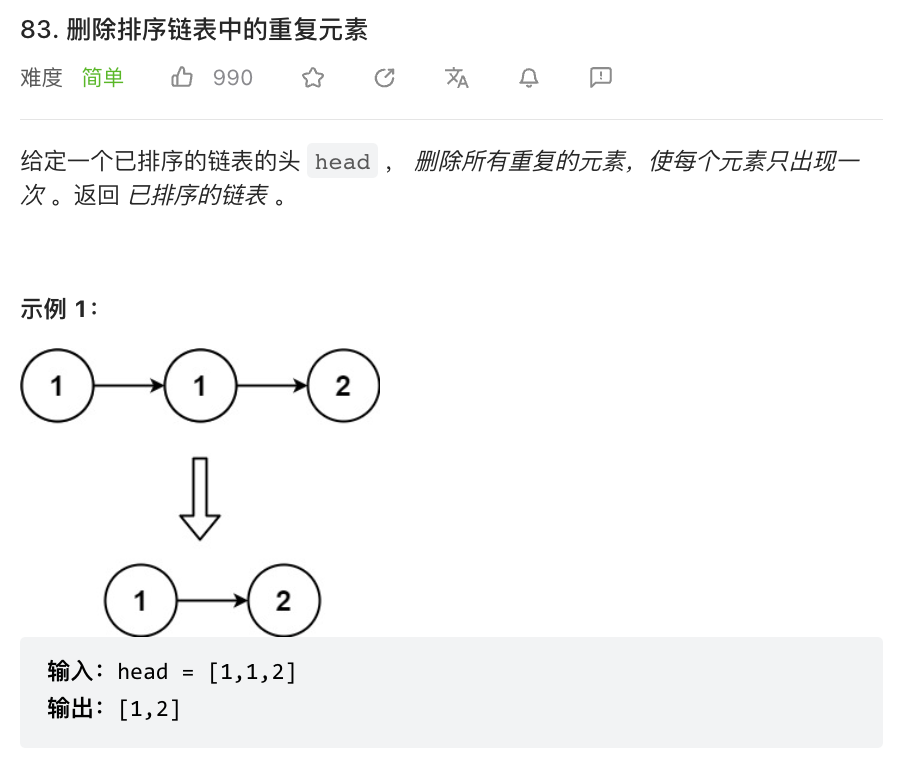
⭐️删除排序链表中的重复元素（力扣 83）

题目描述

思路（双指针）

这道题和上一道题的数据去重几乎一样，唯一的区别就是把更新元素的操作变成了更新指针而已。

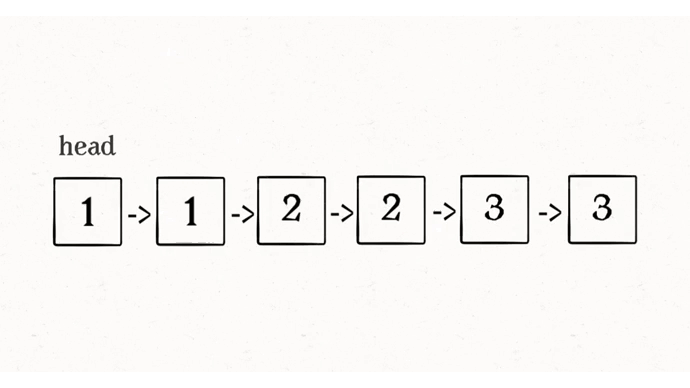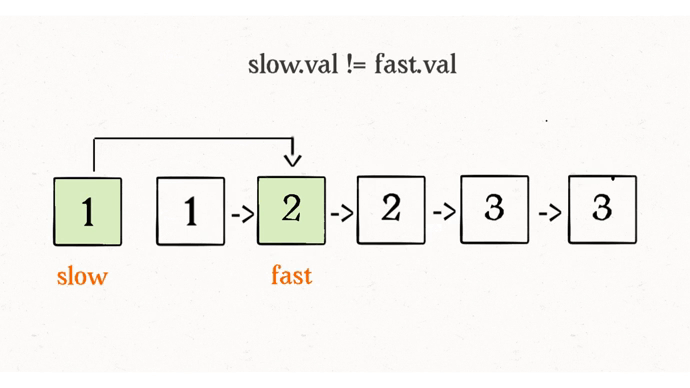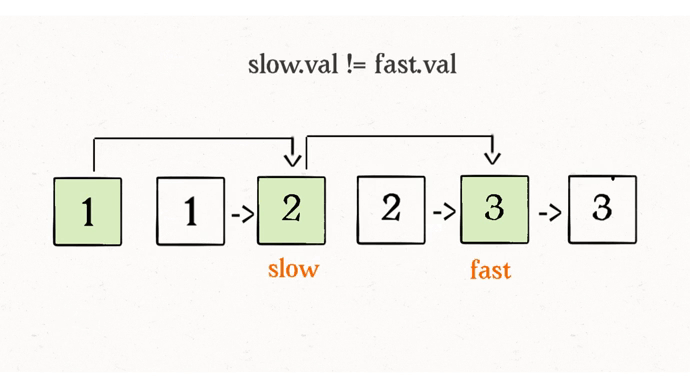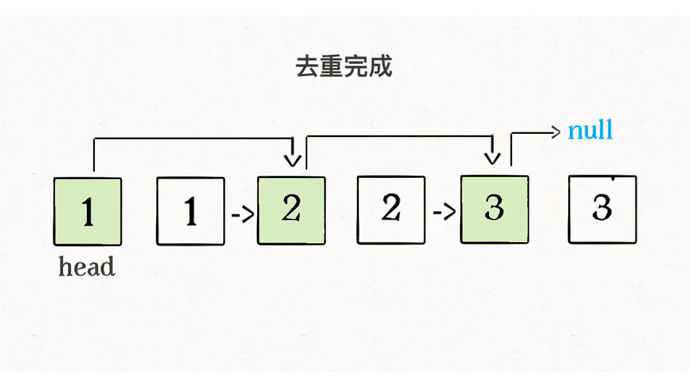
可能会有读者会问，图中的链表节点仍旧挂在那里，这有被删除吗？这就不得不提到 Java 的垃圾回收机制了，对于这些不可达（或者说悬空）的链表节点，JVM 会自动回收。如果你使用的 C++ 这类没有自动垃圾回收机制的语言，你需要在代码中手动释放掉那些节点。

参考代码

public ListNode deleteDuplicates(ListNode head) {
    // 空链表直接返回
    if (head == null) {
        return head;
    }
    ListNode slow = head, fast = head;
    while (fast != null) {
        if (fast.val != slow.val) {
            slow.next = fast; // help GC
            slow = slow.next;
        }
        fast = fast.next;
    }
    // 别忘了这个
    // 断开与后面重复元素的连接
    slow.next = null;
    return head;
}

时间复杂度

\(O(n)\)

n 是链表长度，遍历一遍链表。

空间复杂度

\(O(1)\)

只用到了常数个变量。

删除排序链表中重复的元素II（牛客）

题目描述

思路（双指针）

我们直接讲解进阶思路，也就是使用双指针的方法去解决。

为了便于处理删除第一个节点的情况，我们在链表的前面添加一个虚拟头节点。

我们要知道一点，在升序链表中所有重复的节点都是在一起的。利用这个特性，我们每次比较相邻的两个节点，如果两个节点元素相同，我们就再开一个循环将这段所有相同的节点都遍历过去。

然后让在这一连串相同的节点的前序节点，连上后续第一个不同的节点就可以啦。

最后返回时去掉虚拟头节点即可。

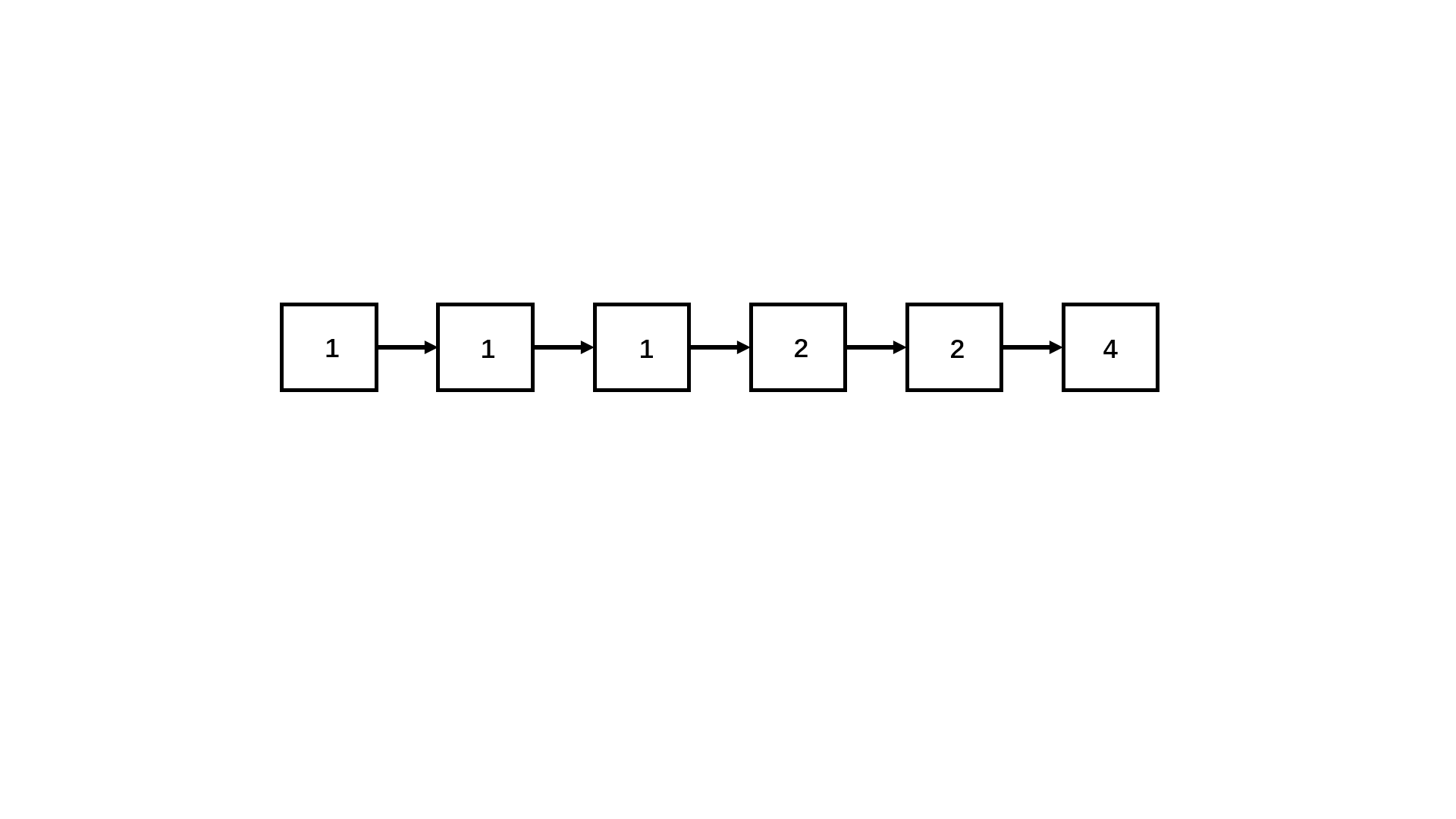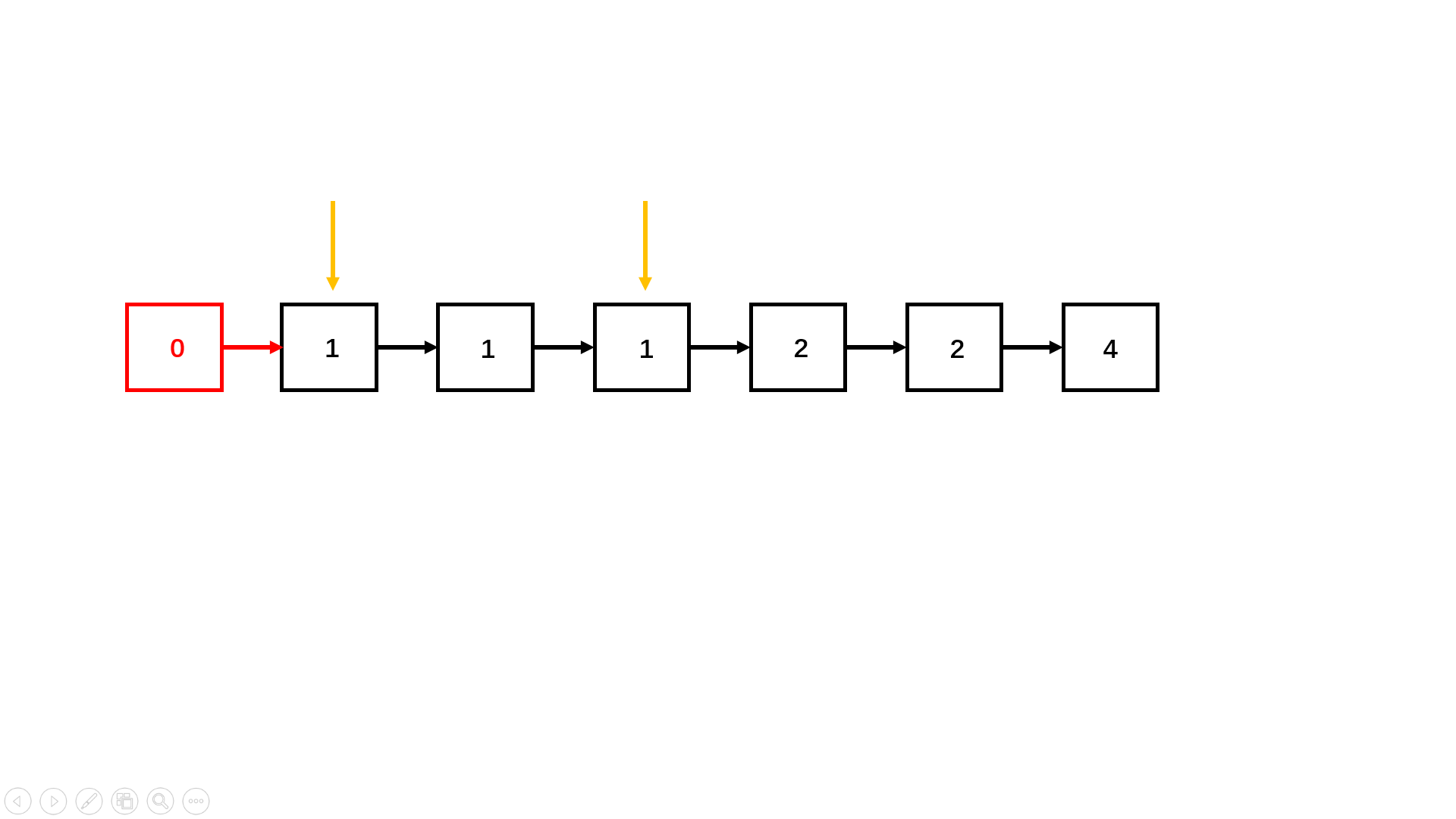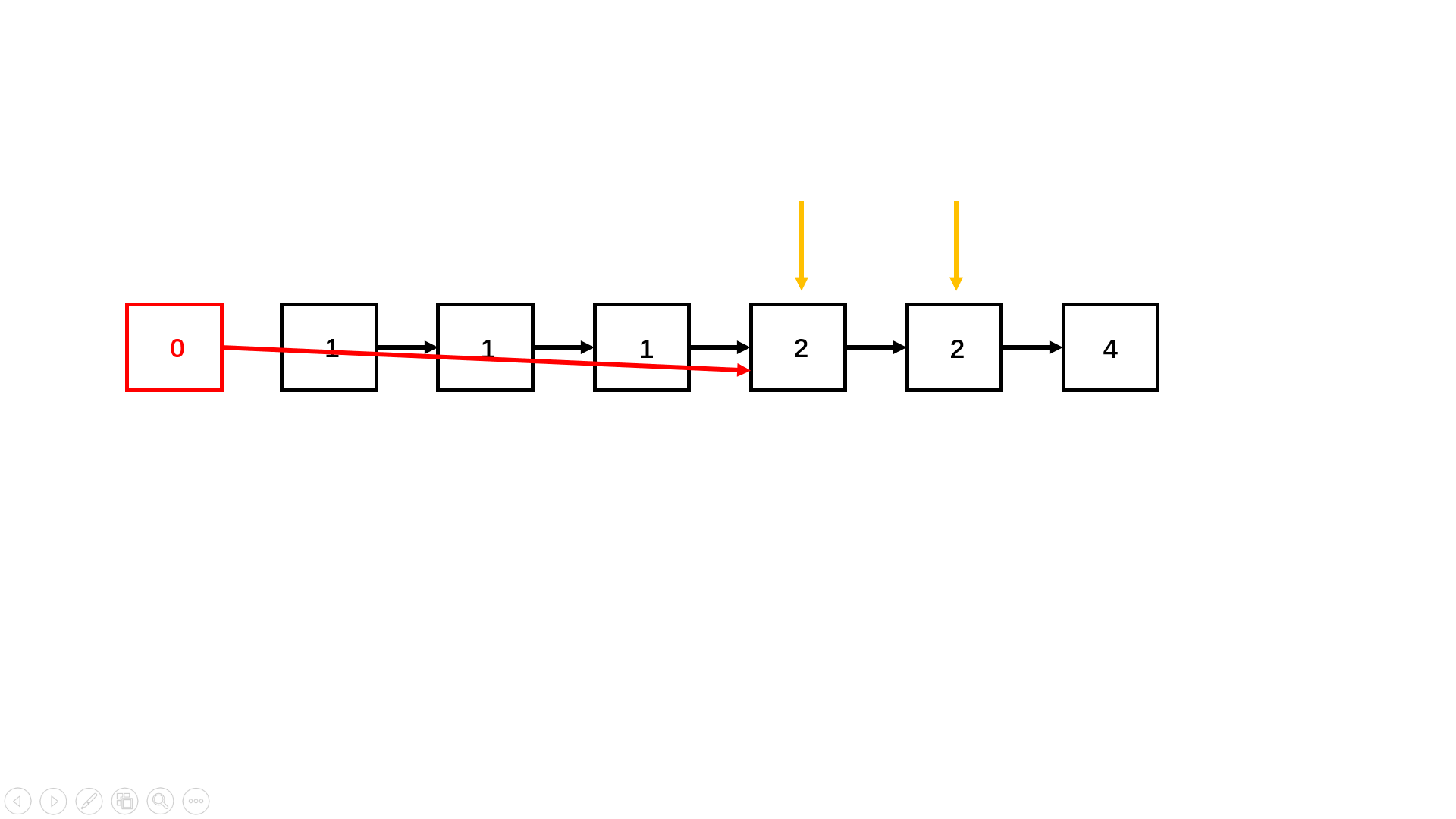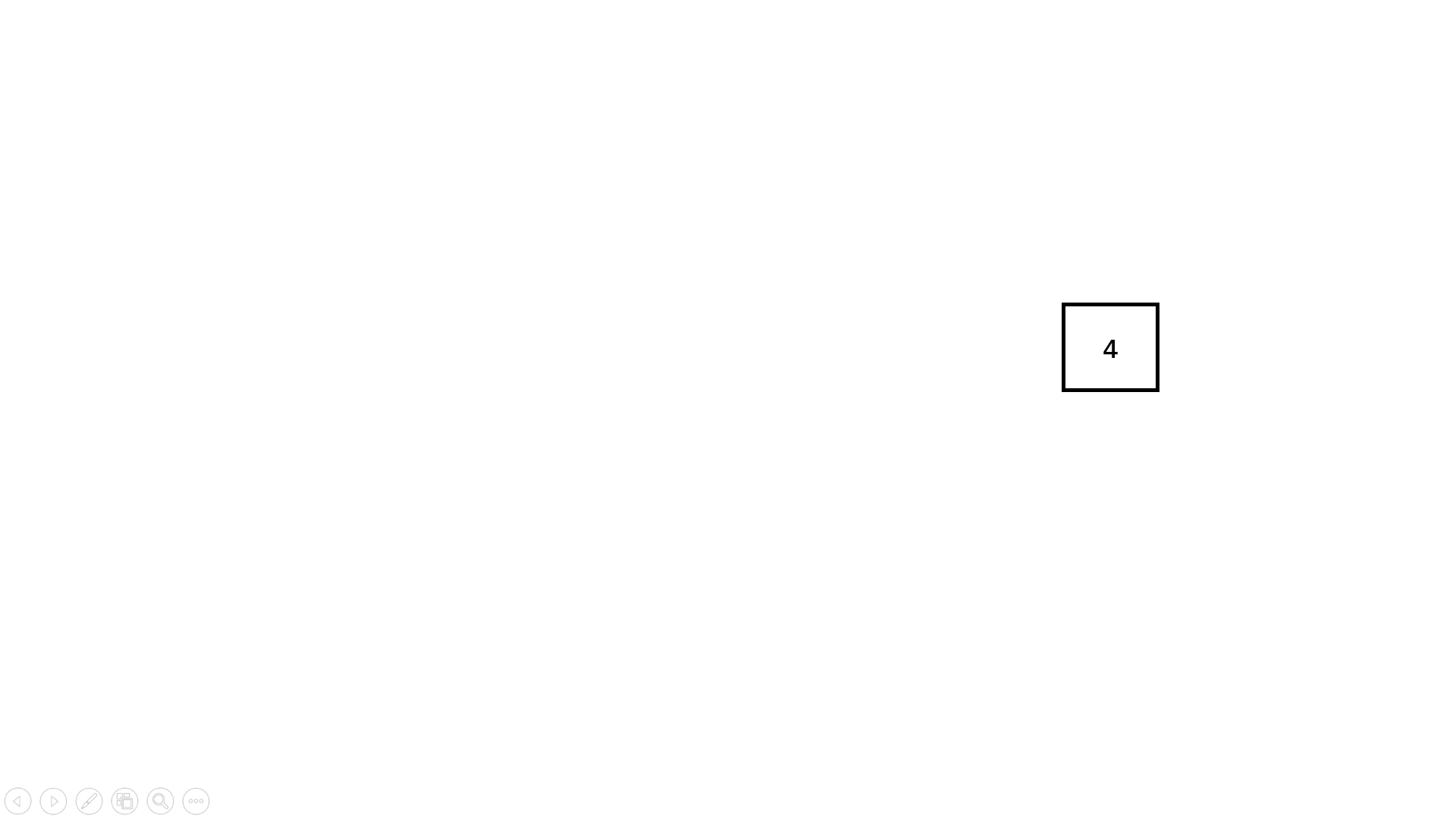
参考代码

public ListNode deleteDuplicates (ListNode head) {
    // 空链表直接返回
    if (head == null) {
        return head;
    }
    // 添加虚拟头节点，便于处理删除第一个链表节点的情况
    ListNode dummy = new ListNode(-1);
    dummy.next = head;
    
    ListNode p = dummy;
    // 双指针: p.next, p.next.next
    while (p.next != null && p.next.next != null) {
        // 如果相邻两节点值相同
        if (p.next.val == p.next.next.val) {
            // 记录值
            int tmp = p.next.val;
            // 新开循环，将所有相同的节点都跳过
            while (p.next != null && p.next.val == tmp) {
                p.next = p.next.next;
            }
        } else {
            p = p.next;
        }
    }
    // 返回时，去掉虚拟头节点
    return dummy.next;
}

虽然有两个 while 循环，但是我们只遍历了一次链表哦，内部的 while 循环帮助我们跳过了所有相同的节点，然后这些节点就不会再被访问了。

时间复杂度

\(O(n)\)

n 为链表节点数，只遍历了一次链表。

空间复杂度

\(O(1)\)

常数个变量。

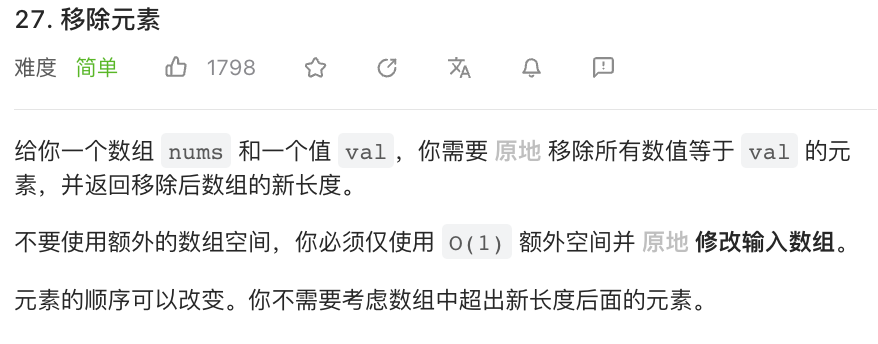
⭐️移除元素（力扣27）

题目描述

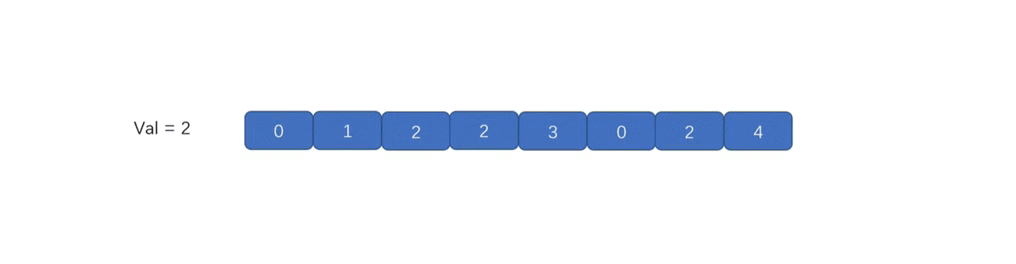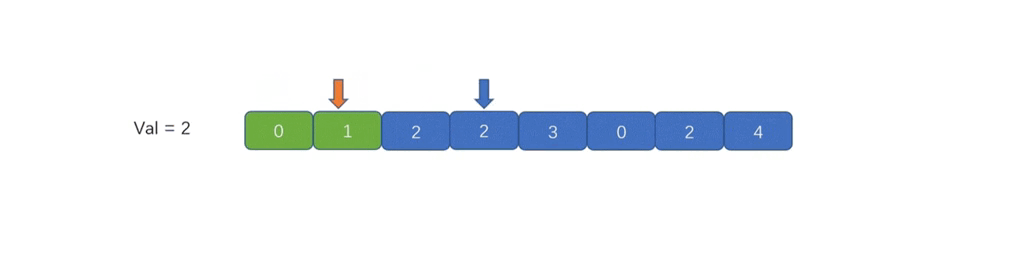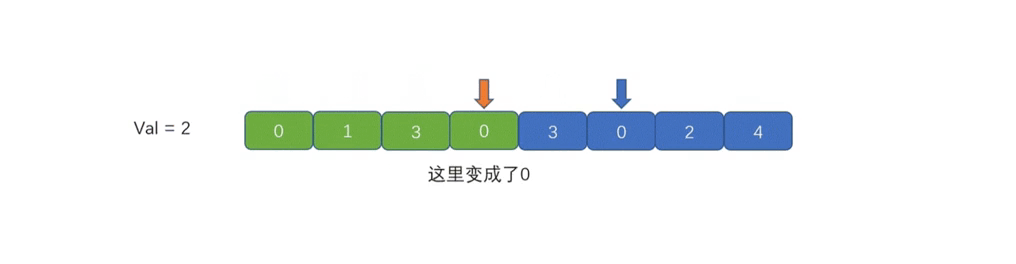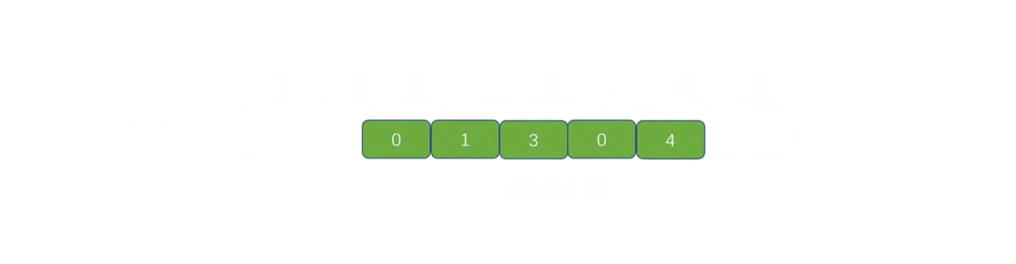
思路（双指针）

这道题和去重不同，我们需要原地删除指定元素。我们依旧准备快慢两个指针，快指针向前遍历，如果快指针 fast 遇到了指定元素，直接跳过；如果没有遇到指定元素，那么就要用 fast 处的元素值更新 slow 处的元素值，然后 slow 再前进一步。

参考代码

public int removeElement(int[] nums, int val) {
    if (nums == null || nums.length == 0) {
        return 0;
    }
    int slow = 0, fast = 0;
    while (fast < nums.length) {
        if (nums[fast] != val) {
            // 先更新值，再移动 slow 指针
            nums[slow] = nums[fast];
            slow++;
        }
        fast++;
    }
    return slow;
}

Tips！

在有序数组去重中，我们是先移动 slow 指针，再更新值。在这里我们是先赋值再向前移动 slow 指针。这样可以保证 nums[0...slow-1] 是不包含指定元素的，最后的结果数组长度就是 slow。

时间复杂度

\(O(n)\)

n 是数组的长度。

空间复杂度

\(O(1)\)

只用到了常数个指针变量。

⭐️移动零（力扣283）

题目描述

思路 I（双指针）

思路 1： 第一种思路很简单，借助「移除元素」的方法，把所有为 0 的元素移除，这样 nums[0...slow-1] 就都是不为 0 的元素，然后将nums[slow...nums.length-1] 用 0 填充。

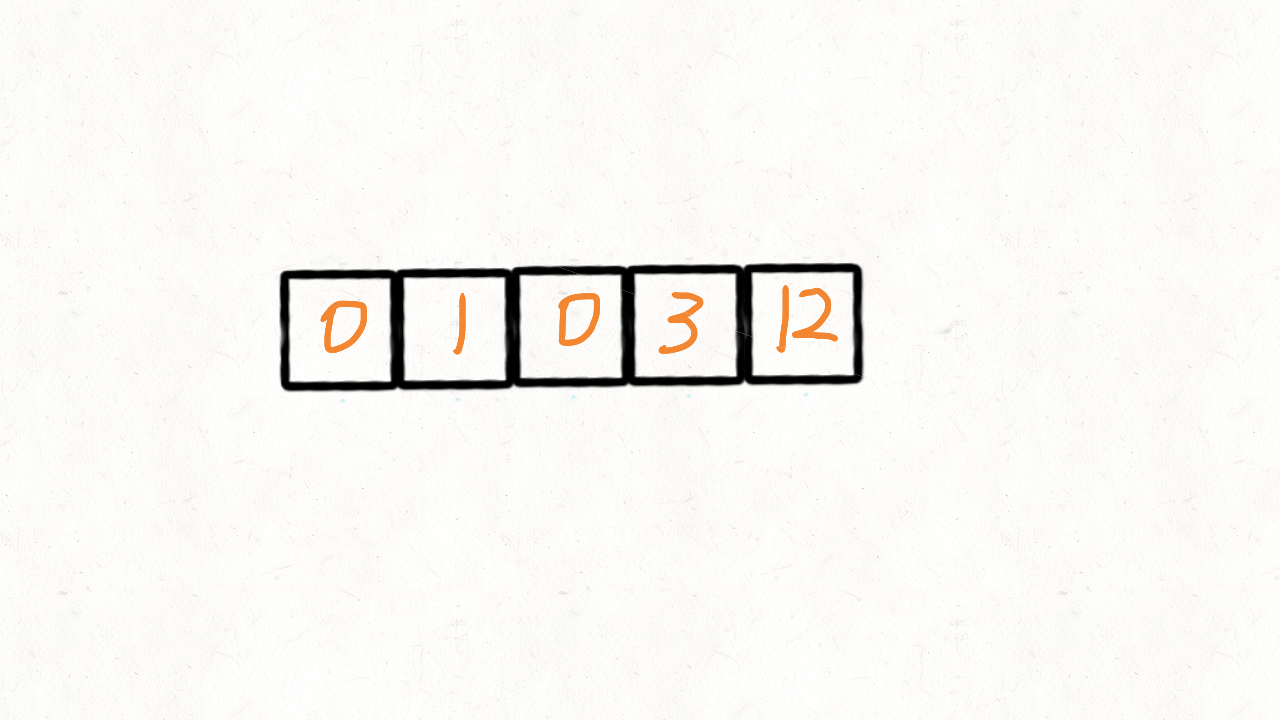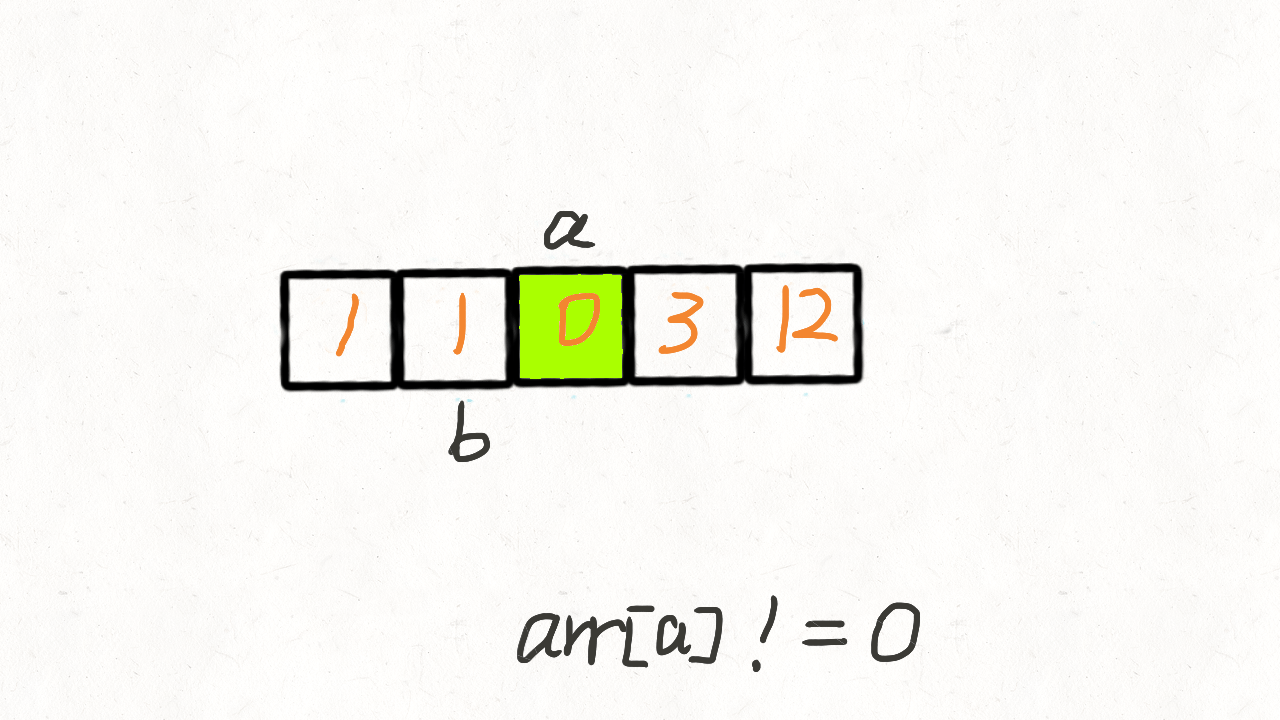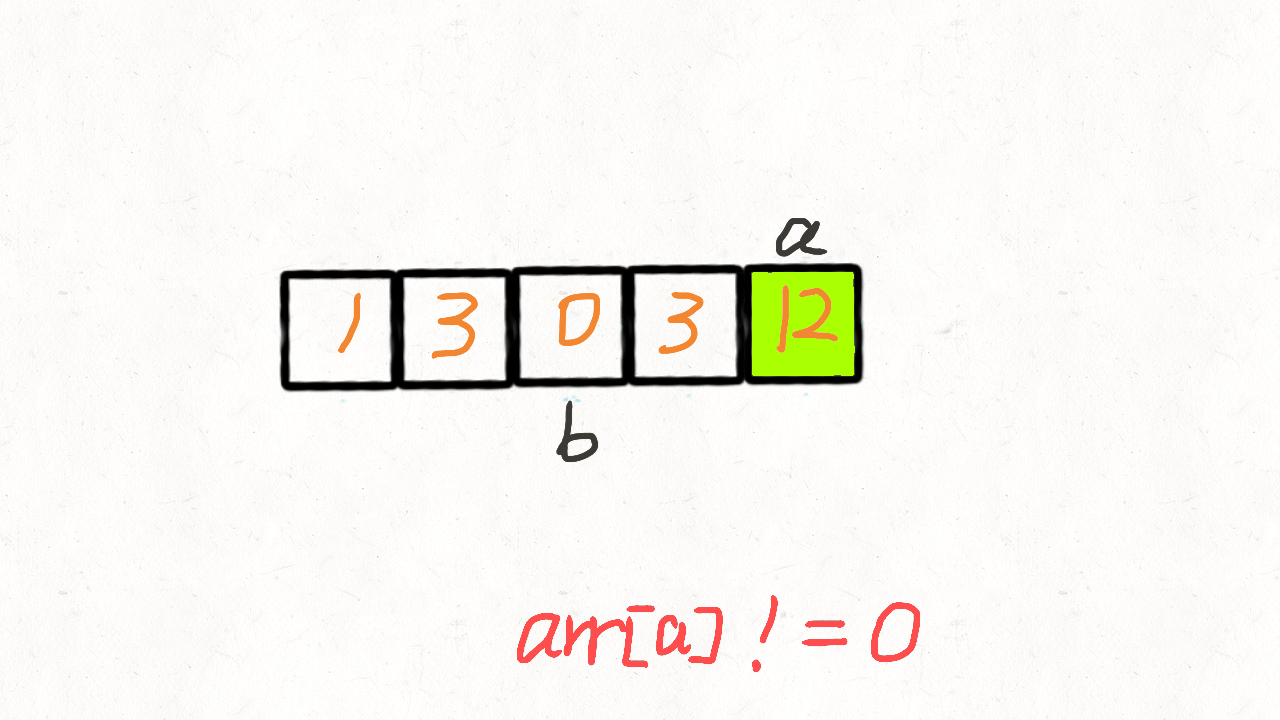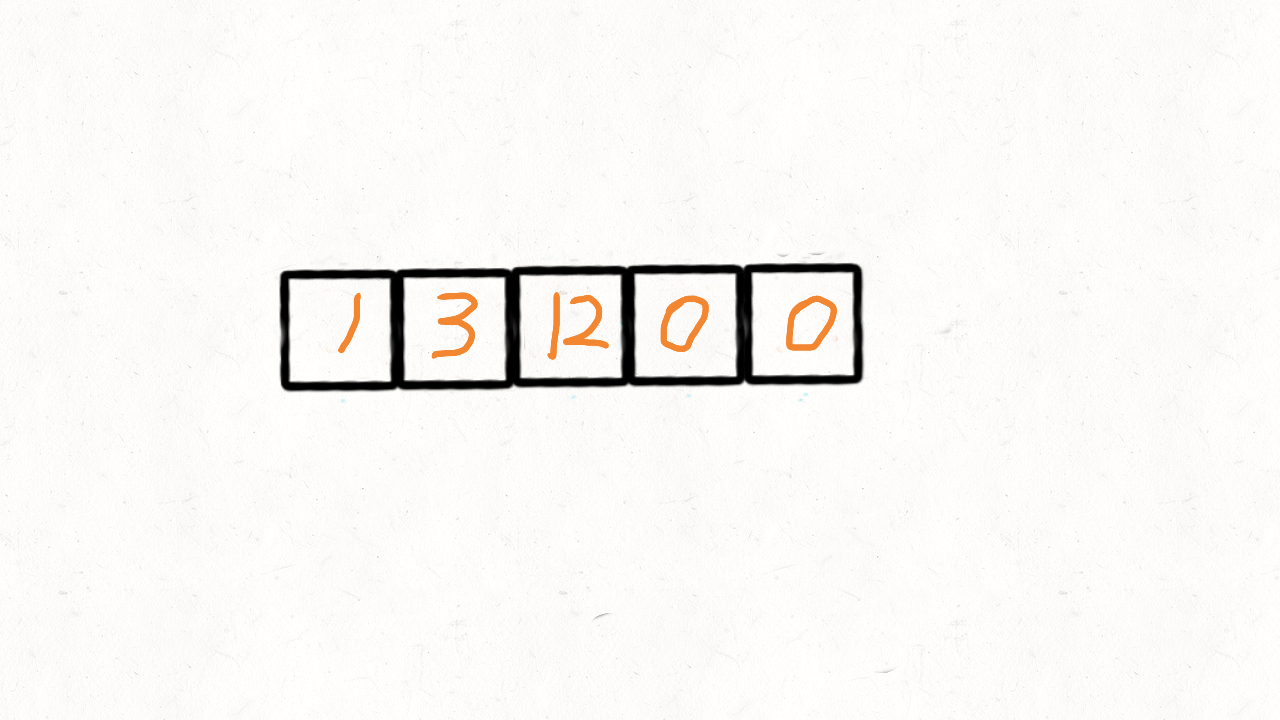
参考代码 I

public void moveZeroes(int[] nums) {
    if (nums == null || nums.length == 0) {
        return;
    }
    // 移除 nums 数组中所有的 0，返回不含 0 的数组长度
    int p = removeElement(nums, 0);
    // 将 nums[p...nums.length-1] 的元素更新为 0
    for (; p < nums.length; p++) {
        nums[p] = 0;
    }
}

public int removeElement(int[] nums, int val) {
    if (nums == null || nums.length == 0) {
        return 0;
    }
    int slow = 0, fast = 0;
    while (fast < nums.length) {
        if (nums[fast] != val) {
            nums[slow] = nums[fast];
            slow++;
        }
        fast++;
    }
    return slow;
}

时间复杂度 I

\(O(n)\)

空间复杂度 I

\(O(1)\)

思路 II（双指针）

这个思路借助了快速排序的思想，快速排序首先要确定一个待分割的元素做中间点 x，然后把所有 <= x 的元素放在 x 的左边，> x 的元素放在 x 的右边。

在这道题中，我们将 0 作为中间点，不等于 0 的放在其左边，等于 0 的放在其右边。

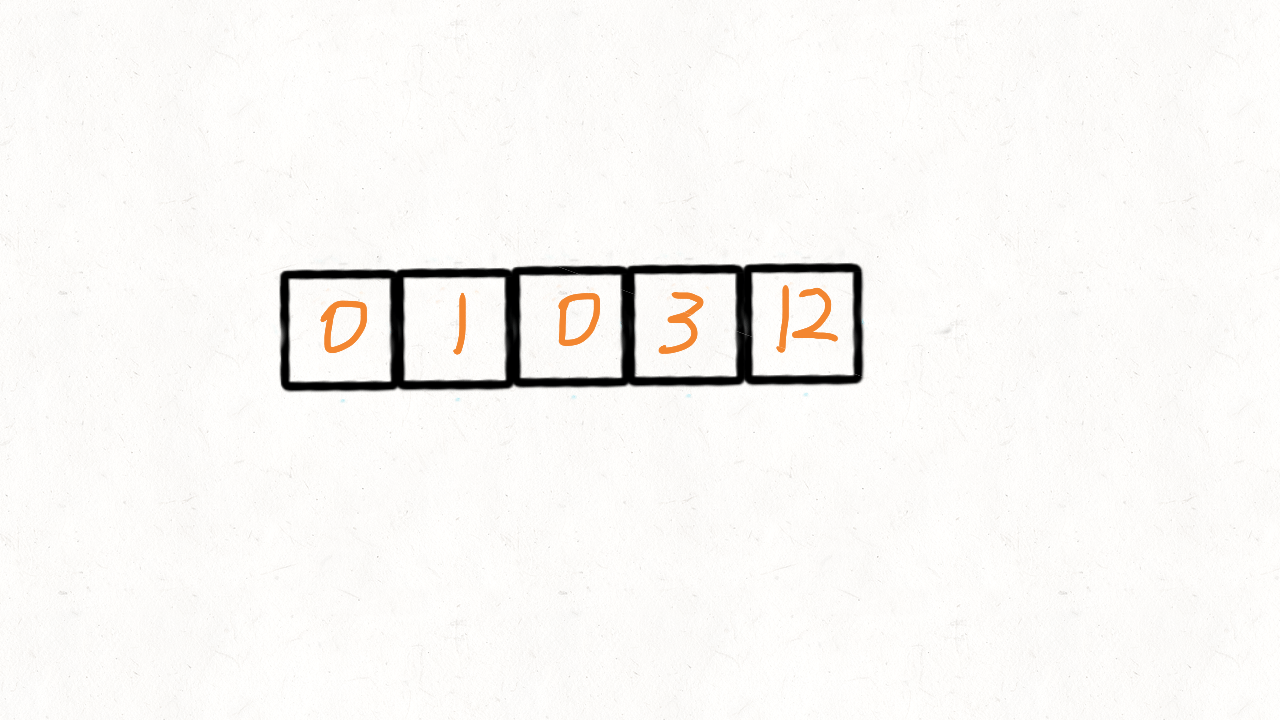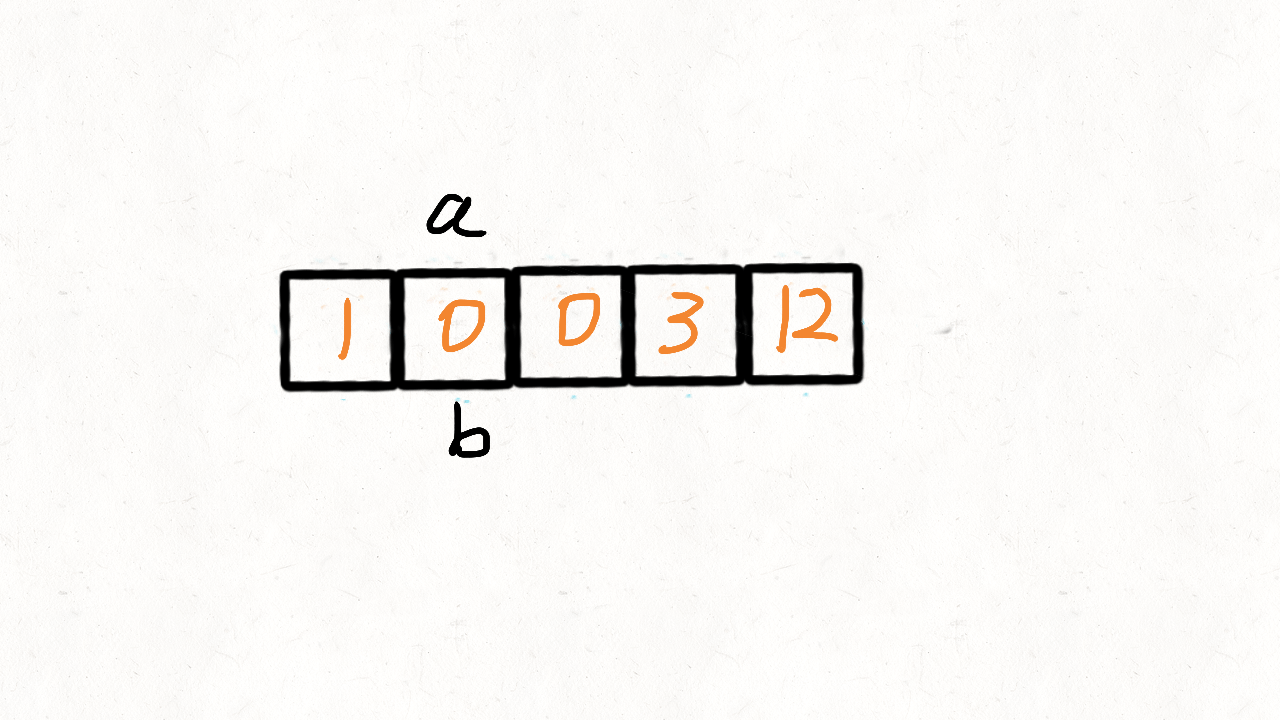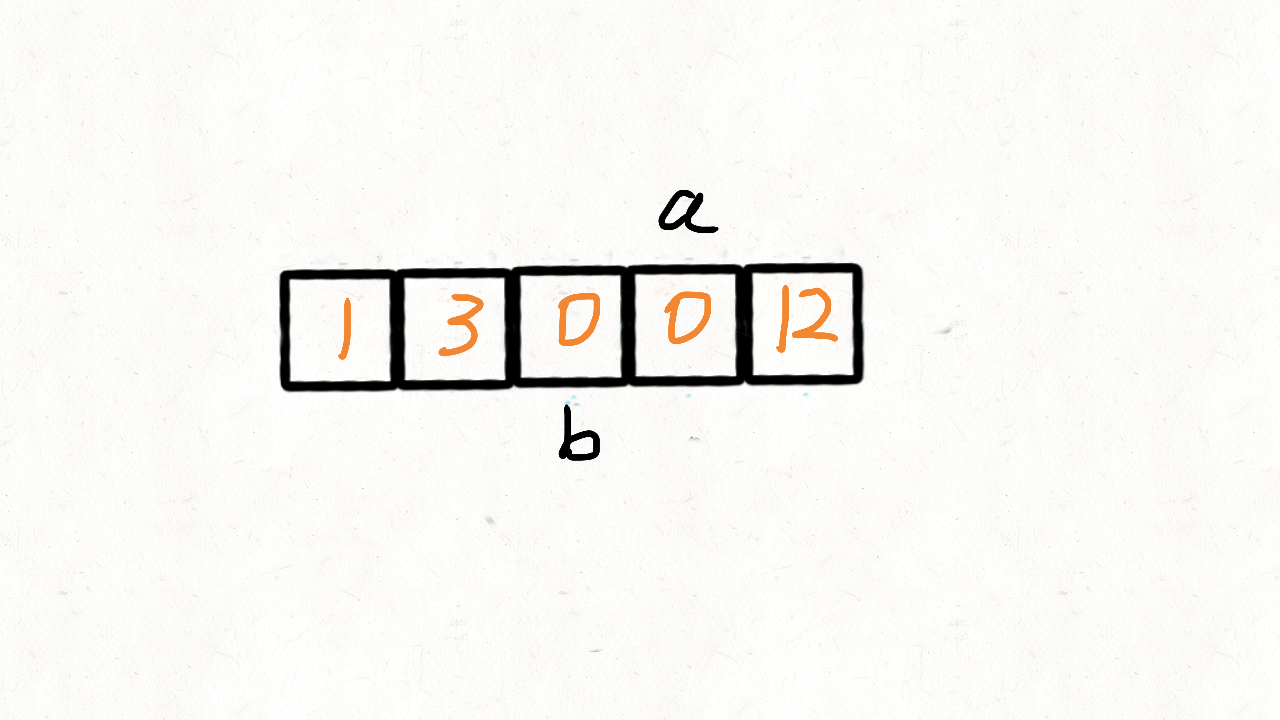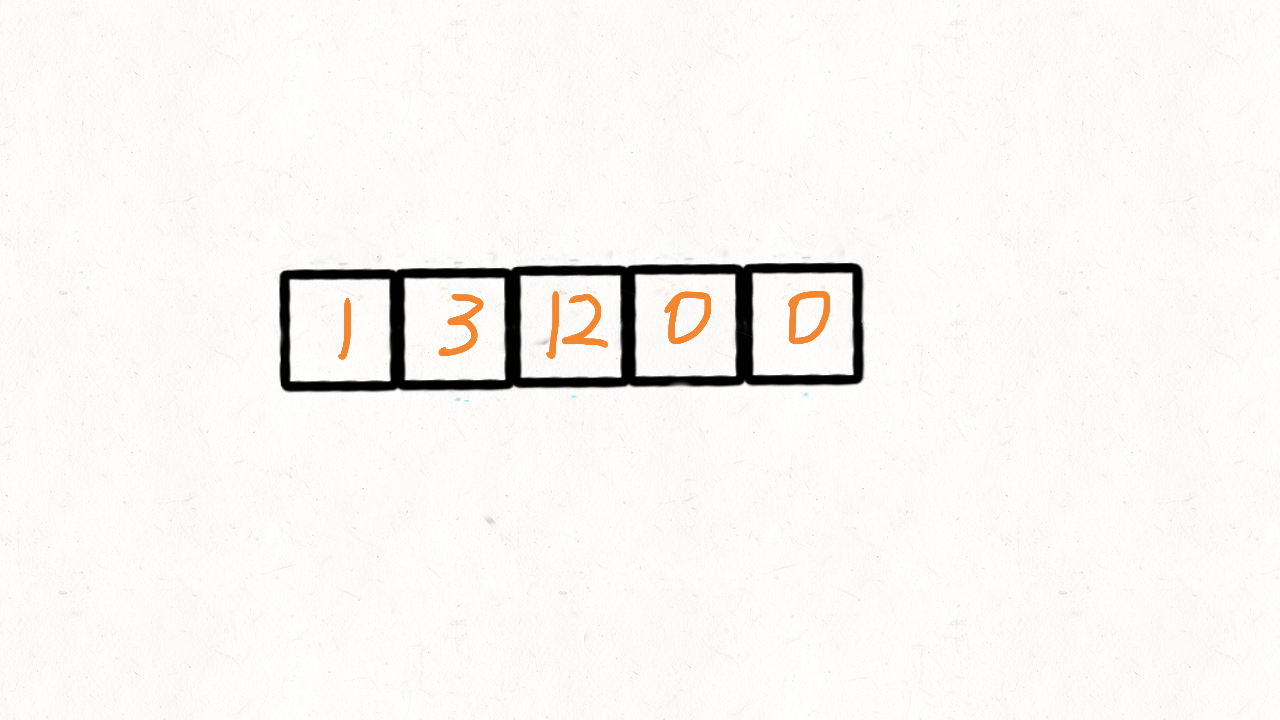
参考代码 II

public void moveZeroes(int[] nums) {
    if (nums == null || nums.length == 0) {
        return;
    }
    int slow = 0, fast = 0;
    while (fast < nums.length) {
        if (nums[fast] != 0) {
            int tmp = nums[fast];
            // 不等于 0 的放在左边
            nums[fast] = nums[slow];
            nums[slow] = tmp;
            slow++;
        }
        // 等于 0 的直接跳过，相当于放在右边
        fast++;
    }
}

时间复杂度 II

\(O(n)\)

空间复杂度 II

\(O(1)\)

⭐️滑动窗口算法

滑动窗口算法是快慢指针演化而来，我们会在后续专门用一篇文章讲解该算法。

滑动窗口算法的核心就是使用 left 和 right 两个指针，left 指针在后，right 指针在前，两个指针中间部分就是「窗口」，然后根据具体情况确定扩大和缩小「窗口」以解决问题。

左右指针技巧

⭐️二分搜索问题

谈到左右指针技巧的使用，最经典的当属二分搜索算法。我已在手撕算法必备技巧（壹）—— 二分搜索这篇文章全面阐述了二分搜索如何寻找一个数，或者寻找左右两边界问题。

⭐️反转字符数组（力扣344）

题目描述

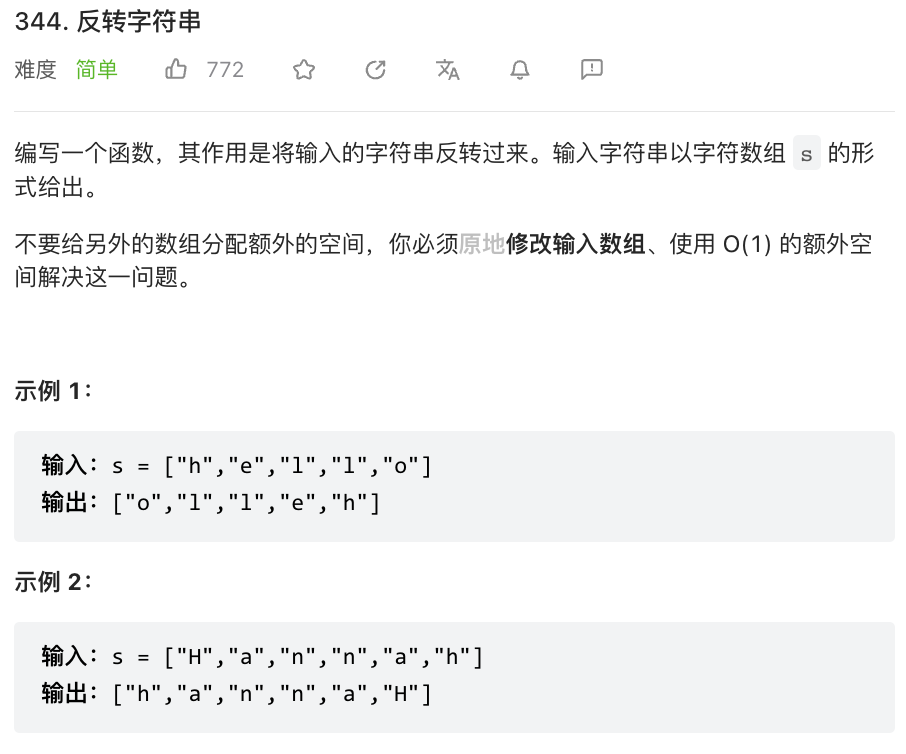
思路（左右指针）

这道题很简单，使用左右指针，初始化分别指向 0 和 s.length - 1 ，然后交换并移动指针就可以啦。

参考代码

public void reverseString(char[] s) {
    int left = 0, right = s.length - 1;
    while (left < right) {
        swap(s, left, right);
        left++;
        right--;
    }
}
public void swap(char[] s, int i, int j) {
    char tmp = s[i];
    s[i] = s[j];
    s[j] = tmp;
}

时间复杂度

\(O(n)\)

空间复杂度

\(O(1)\)

⭐️有序数组的平方（力扣977）

题目描述

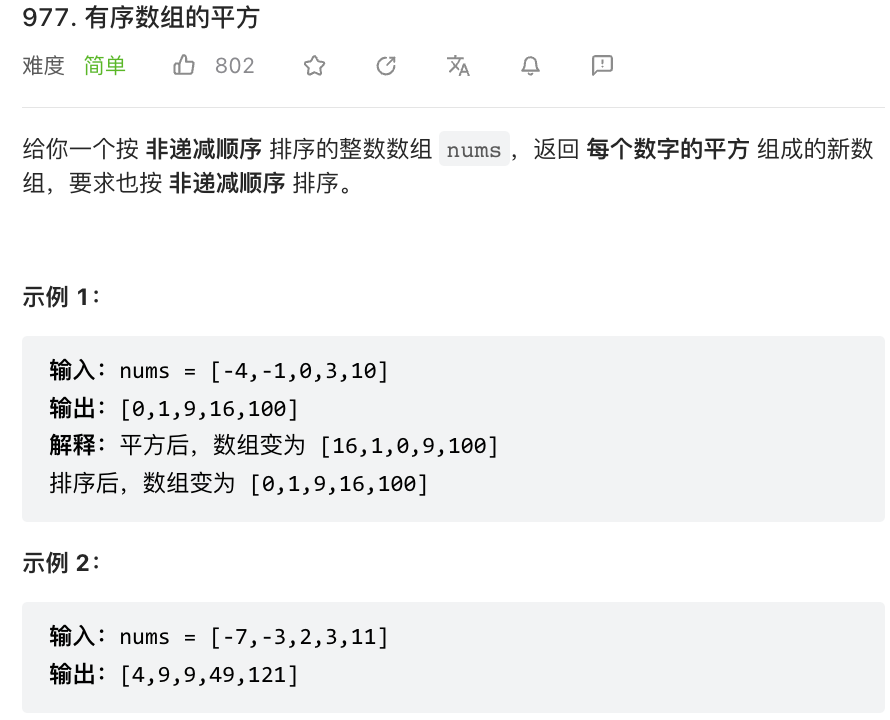
思路（左右指针）

最简单的方法就是计算数组中的每个数，然后进行排序。这种算法的时间复杂度是 \(O(nlogn)\)，而且没有使用到数组是有序的这个条件。

更好地做法是，使用「左右指针」的方法，不仅可以让时间复杂度降到 \(O(n)\) 级别，还利用到了数组是有序的这个条件。

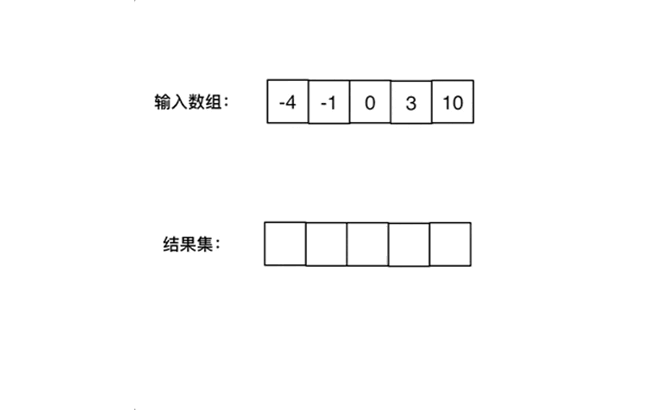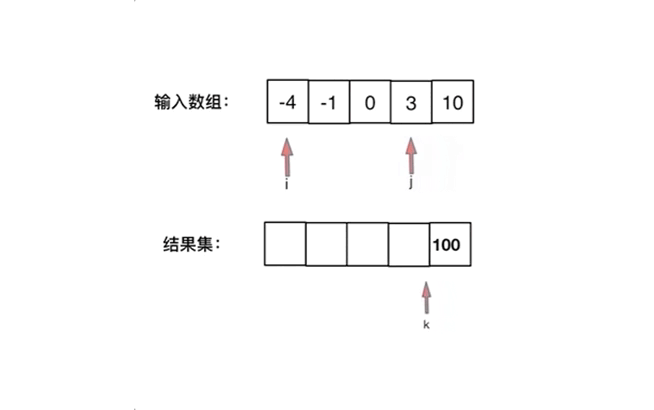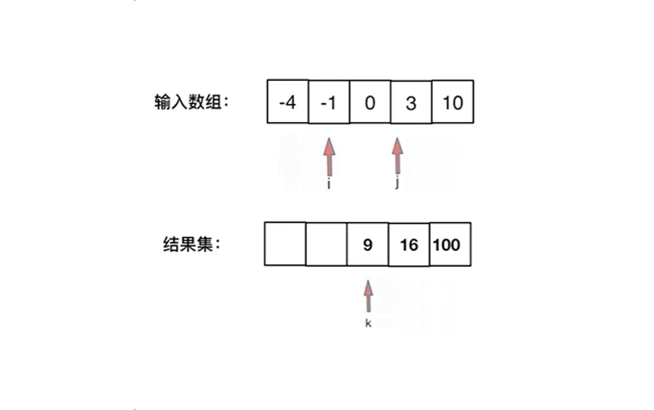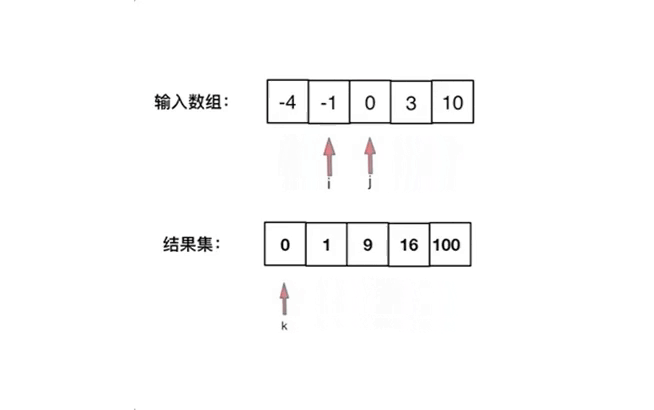
我们新建一个结果集数组，然后初始化左右指针，分别指向输入数组的 0 和 n - 1，每次比较左右指针元素的平方大小。选择平方后更大的数逆序放入结果集中，然后被选择的指针和结果集指针进行移动。

参考代码

public int[] sortedSquares(int[] nums) {
    int n = nums.length;
    // 空数组直接返回
    if (nums == null || n == 0) {
        return nums;
    }
    // 结果集数组
    int[] res = new int[n];
    // 输入数组的左右指针，以及结果集的指针
    int left = 0, right = n - 1, i = n - 1;
    while (left < right) {
        // 谁的平方大，谁逆序放入结果集数组中
        if (nums[left] * nums[left] <= nums[right] * nums[right]) {
            res[i] = nums[right] * nums[right];
            right--;
        } else {
            res[i] = nums[left] * nums[left];
            left++;
        }
        i--;
    }
    // 处理 left == right 的情况
    res[i] = nums[left] * nums[left];
    return res; 
}

时间复杂度

\(O(n)\)

n 是 nums 数组的长度

空间复杂度

\(O(1)\)

除了必要的用于存储结果集数组的空间，只另外用到了常数个变量。

⭐️N数之和问题

N 数之和问题包括两数之和、三数之和、... N 数之和。该问题会在后续单独出一篇文章进行讲解。

总结

本文主要讲解了双指针的左右指针、快慢指针是如何在数组问题中使用的，也给自己挖了两个坑需要去填，一个是快慢指针中的滑动窗口算法问题，另一个是左右指针中的 N 数之和问题。

希望以上内容可以帮助到你，让你变得更强，大家加油！

参考资料

力扣网
牛客网
算法基地 - github
labuladong 的算法小抄
代码随想录