二叉树与递归的框架思维「详解版」

发表于 更新于 分类于 ， ， 本文字数： 5.7k 阅读时长 ≈ 21 分钟 阅读次数：

二叉树解题思维分两类：

  1. 是否可以通过遍历一遍二叉树得到答案？

    如果可以，用一个 traverse 函数配合外部变量来实现，这叫 「遍历」的思维模式。

  2. 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？

    如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

无论哪种思维模式，我们都需要思考：

如果单独抽出一个二叉树节点，它需要做什么事情？需要在什么时候（前/中/后序位置）做？其他的节点不用你操心，递归函数会帮你在所有节点上执行相同的操作。

本文解决了如下题目：

力扣第 104 题「二叉树的最大深度」

力扣第 144 题「二叉树的前序遍历」

力扣第 543 题「二叉树的直径」

剑指 Offer 第 55 题 「二叉树的深度」

二叉树的重要性

快速排序和归并排序的本质

  • 快速排序：二叉树前序遍历

  • 归并排序：二叉树后序遍历

快速排序的逻辑和框架

算法逻辑

若要对 nums[lo...hi] 进行排序，我们先找一个分界点 p，通过交换元素使得 nums[lo...p-1] 都 <= nums[p]，且 nums[p+1...hi] 都 > nums[p]，然后递归地去 nums[lo...p-1] 和 nums[p+1...hi] 中寻找新的分界点，最后这个数组就被排序了。

代码框架
1
2
3
4
5
6
7
8
9
10
// 定义：排序 nums[lo...hi]
void sort(int[] nums, int lo, int hi) {
    /****** 前序遍历位置 ******/
    // 通过交换元素构建分界点 p
    int p = partition(nums, lo, hi);
    /************************/
    
    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi)
}

先构造分界点，然后去左右子数组构造分界点，这不就是一个二叉树的前序遍历吗？

归并排序的逻辑和框架

算法逻辑

若要对 nums[lo...hi] 进行排序，我们先对 nums[lo...mid] 进行排序，再对 nums[mid+1...hi] 排序，最后把这两个有序的子数组合并成整个数组就排好序了。

代码框架
1
2
3
4
5
6
7
8
9
10
11
12
13
// 定义：排序 nums[lo...hi]
void sort(int[] nums, int lo, int hi) {
    int mid = lo + ((hi - lo) >> 1);
    // 排序 nums[lo...mid]
    sort(nums, lo, mid);
    // 排序 nums[mid+1...hi]
    sort(nums, mid + 1, hi);
    
    /****** 后序位置 ******/
    // 合并 nums[lo...mid] 和 nums[mid+1...hi]
    merge(nums, lo, mid, hi);
    /********************/
}

先对左右子数组进行排序，然后合并（类似合并有序链表的逻辑），这不就是二叉树的后序遍历嘛，同时也是分治算法思想的体现呀。

二叉树的算法思想运用广泛，甚至可以说，只要涉及递归，都可以抽象成二叉树问题。

深入理解前中后序

三个问题

先思考 3 个问题：

  1. 二叉树的前中后序遍历是什么？仅仅是三个顺序不同的 List 吗？
  2. 后序遍历有什么特殊之处？
  3. 多叉树为什么没有中序遍历？
二叉树遍历框架

首先，看一下二叉树的遍历框架：

1
2
3
4
5
6
7
8
9
void traverse(TreeNode root) {
    if (root == null)
        return;
    // 前序位置
    traverse(root.left);
    // 中序位置
    traverse(root.right);
    // 后序位置
}

先不管所谓前中后序，单看 traverse 函数，它在做什么事情？

其实，它就是一个能够遍历二叉树所有节点的一个函数，和遍历数组或者链表本质上没有区别：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 迭代遍历数组
void traverse(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
        
    }
}

// 递归遍历数组
void traverse(int[] arr, int i) {
    if (i == arr.length)
        return;
    // 前序位置
    traverse(arr, i + 1);
    // 后序位置
}

// 迭代遍历单链表
void traverse(ListNode head) {
    for (ListNode p = head; p != null; p = p.next) {
        
    }
}

// 递归遍历单链表
void traverse(ListNode head) {
    if (head == null)
        return;
    // 前序位置
    traverse(head.next);
    // 后序位置
}

单链表和数组的遍历可以是迭代的，也可以是递归地，二叉树这种结构无非就是二叉链表，由于没办法简单改写成迭代形式，所以一般说二叉树的遍历框架都是指递归的形式。

值得注意的是，只要是递归形式的遍历，都可以有前序位置和后序位置，分别在递归之前和递归之后。

所谓前序位置，就是刚进入一个节点（元素）的时候，后序位置就是即将离开一个节点（元素）的时候，那么进一步，你把代码写在不同位置，代码执行的时机也不同：

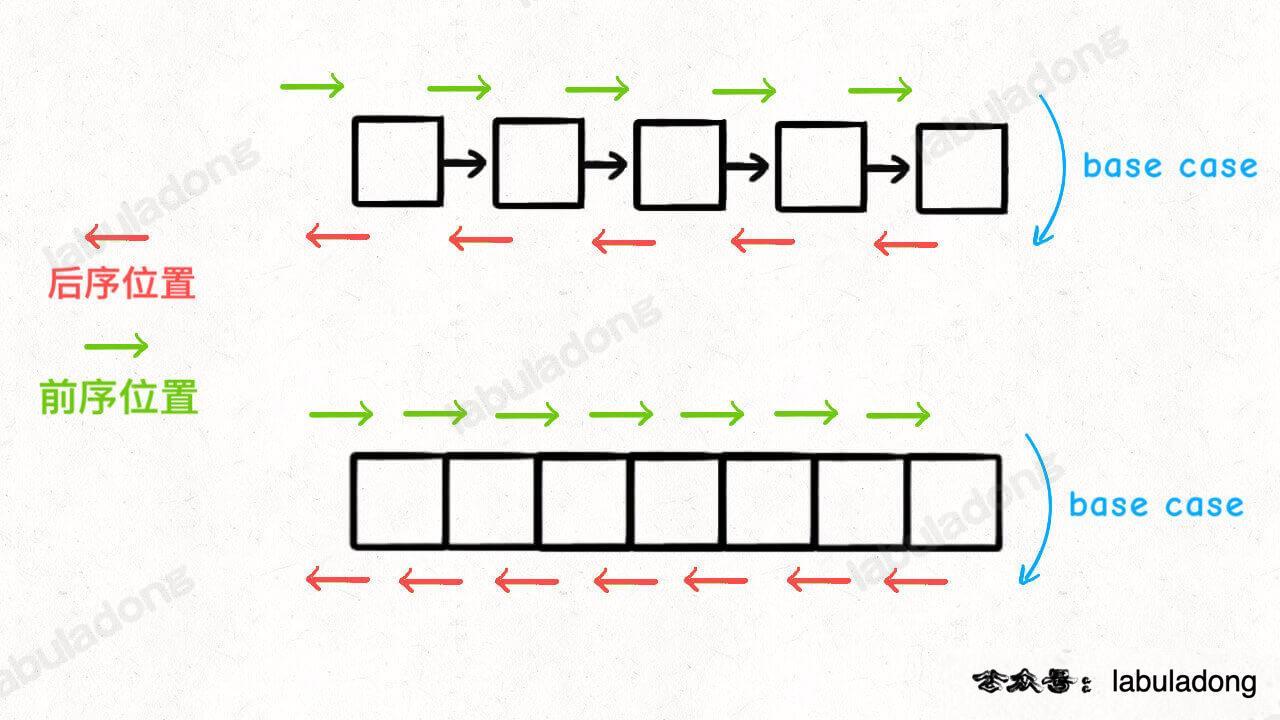
代码执行时机

如果让你倒序打印一条单链表上所有节点的值，你如何实现？

如果使用递归来实现的话，可以利用后序位置来操作：

1
2
3
4
5
6
7
8
void traverse(ListNode head) {
    if (head == null)
        return;
    // 前序位置
    traverse(head.next);
    // 后序位置
    print(head.val);
}

结合上面那张图，可以知道这段代码之所以能实现倒序打印单链表的本质是：利用递归的堆栈帮你实现了倒序遍历的效果。

前中后序位置的特殊性

回到二叉树，二叉树不过多了一个中序位置罢了。

前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点，绝不仅仅是三个顺序不同的 List。

  • 前序位置的代码在刚刚进入一个二叉树节点的时候执行；
  • 后序位置的代码在将要离开一个二叉树节点的时候执行；
  • 中序位置的代码在一个二叉树节点左子树都遍历完，即将开始遍历右子树的时候执行。

注意文中的用词，一直在强调前中后序「位置」，就是要和常说的前中后序「遍历」有所区别：我们可以在前序位置写代码，往一个 List 里面塞元素，那最后得到的就是前序遍历结果；但并不是说你就不可以写更复杂的代码做更复杂的事。

画成图，前中后序三个位置在二叉树上的样子如下：

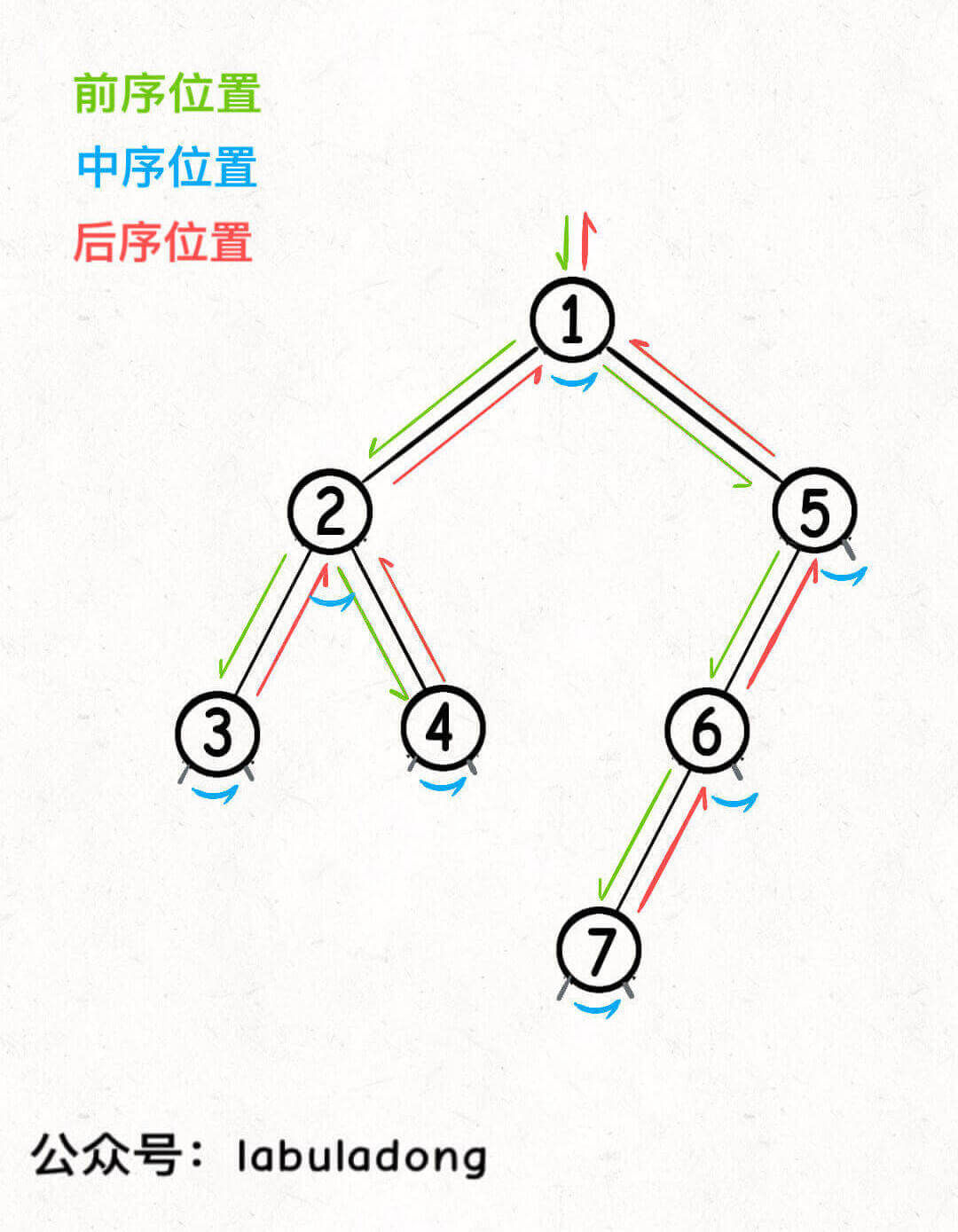
二叉树的前中后序的位置

可以发现，每个节点都有唯一属于自己的前中后序位置，因此前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点。

多叉树没有中序位置的原因

这也就是为什么多叉树没有中序位置，因为二叉树的每个节点只会进行唯一一次左子树切换右子树，而多叉树节点可能有很多子节点，会多次切换子树去遍历，所以多叉树节点没有「唯一」的中序遍历位置。

二叉树的所有问题，就是让你在前中后序位置注入巧妙的代码逻辑，去达到自己的目的，你只需要单独思考每一个节点应该做什么，其他的不用你管，抛给二叉树遍历框架，递归会在所有节点上做相同的操作。

图论算法将二叉树的遍历框架扩展到了图，并以遍历为基础实现了图论的各种经典算法。

两种解题思路

二叉树题目的递归解法可以分两类思路，第一类是遍历一遍二叉树得出答案，第二类是通过分解问题计算出答案，这两类思路分别对应着回溯算法核心框架和动态规划核心框架。

函数命名习惯

二叉树中用遍历思路解题时函数签名一般是void traverse(...)，没有返回值，靠更新外部变量来计算结果。而用分解问题思路解题时函数名根据该函数具体功能而定，而且一般会有返回值，返回值是子问题的计算结果。

与此对应，在回溯算法核心框架中给出的函数签名一般也是没有返回值的 void backtrack(...)。而在动态规划核心框架中给出的函数签名是带有返回值的 dp 函数。这也说明了它俩和二叉树之间有联系。

从二叉树的最大深度看两种解题思路

牛客BM28 二叉树的最大深度，所谓最大深度就是树的根节点到最远叶子节点的最长路径上的节点数，比如输入这棵二叉树，算法应该返回 3：

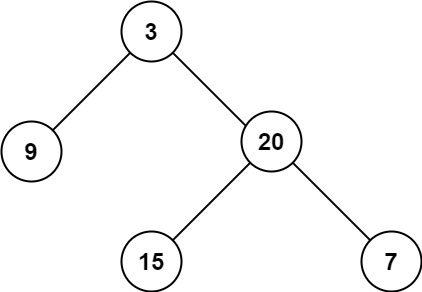
二叉树的最大深度

遍历二叉树得出答案

思路：遍历一遍二叉树，用一个外部变量记录每个节点所在的深度，取最大值就可以得到最大深度，这就是遍历二叉树计算答案的思路。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 记录最大深度
int res = 0;
// 记录遍历到的节点的深度
int depth = 0;
// 主函数
int maxDepth(TreeNode root) {
    traverse(root);
    return res;
}

// 二叉树遍历框架
void traverse(TreeNode root) {
    if (root == null)
        return;
    // 前序位置
    depth++;
    if (root.left == null && root.right == null) {
        // 到达叶子节点，更新最大深度
        res = Math.max(res, depth);
    }
    traverse(root.left);
    // 中序位置
    traverse(root.right);
    // 后序位置
    depth--;
}

为什么需要再前序位置增加 depth，在后序位置减小 depth ?

因为前面说了，前序位置是进入一个节点的时候，后序位置是离开一个节点的时候，depth 记录当前递归到的节点深度，你把 traverse 理解成在二叉树上游走的一个指针，所以当然要这样维护。

至于对 res 的更新，你放到前中后序位置都可以，只要保证在进入节点之后，离开节点之前（即 depth 自增之后，自减之前）就行了。

分解问题得出答案

当然，你也很容易发现一棵二叉树的最大深度可以通过子树的最大深度推导出来，这就是分解问题计算答案的思路。

解法代码如下：

1
2
3
4
5
6
7
8
9
10
11
// 定义：输入根节点，返回这棵二叉树的最大深度
int maxDepth(TreeNode root) {
    if (root == null)
        return 0;
    // 利用定义，计算左右子树的最大深度
    int leftMax = maxDepth(root.left);
    int rightMax = maxDepth(root.right);
    // 整棵树的最大深度 = 左右子树的最大深度取最大值 + 1 (根节点自己)
    int res = Math.max(leftMax, rightMax) + 1;
    return res;
}

只要明确递归函数的定义，这个解法也不难理解，但为什么主要的代码逻辑集中在后序位置？

因为这个思路正确的核心在于，你确实可以通过子树的最大深度推导出原树的深度，所以当然要首先利用递归函数的定义算出左右子树的最大深度，然后推出原树的最大深度，主要逻辑自然放在后序位置。

二叉树的前序遍历

如果理解了最大深度这个问题的两种思路，那么我们在回头看看最基本的二叉树前中后序遍历，比如获取前序遍历结果。

遍历二叉树得出答案

最熟悉的解法就是用「遍历」的思路：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
List<Integer> res = new LinkedList<>();
// 返回前序遍历结果
List<Integer> preorderTraverse(TreeNode root) {
    traverse(root);
    return res;
}
// 二叉树遍历函数
void traverse(TreeNode root) {
    if (root == null)
        return;
    // 前序位置
    res.add(root);
    traverse(root.left);
    traverse(root.right);
}
分解问题得出答案

那么，能否使用「分解问题」的思路，来计算前序遍历的结果？

换句话说，不要用像 traverse 这样的辅助函数和任何外部变量，单纯用题目给的 preorderTraverse 函数递归解题。

我们知道前序遍历的特点是，根节点的值排在首位，接着是左子树的前序遍历结果，最后是右子树的遍历结果。

img

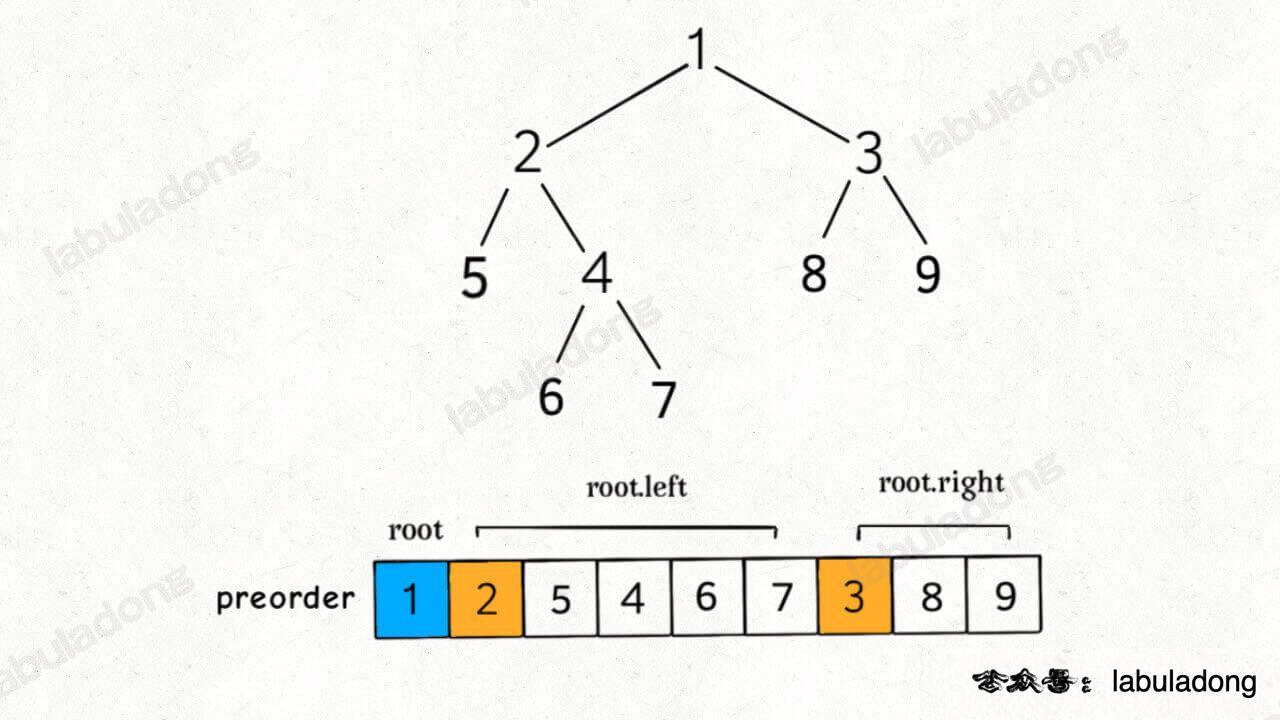
那么，这样就可以分解问题了。

一棵二叉树的前序遍历结果 = 根节点 + 左子树的前序遍历结果 + 右子树的前序遍历结果。

所以，就可以这样实现前序遍历算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
// 定义：输入一棵二叉树的根节点，返回这棵树的前序遍历结果
List<Integer> preorderTraverse(TreeNode root) {
    List<Integer> res = new LinkedList<>();
    if (root == null)
        return res;
    // 前序遍历的结果，root.val 在第一个
    res.add(root.val);
    // 利用函数定义，后面接着左子树的前序遍历结果
    res.addAll(preorderTraverse(root.left));
    // 利用函数定义，后面接着右子树的前序遍历结果
    res.addAll(preorderTraverse(root.right));
    return res;
}

中序和后序遍历也是类似的，只要把 add(root.val) 放到中序和后序对应的位置就行了。

这个解法短小精干，但为什么不常见呢？

一个原因是这个算法的复杂度不好把控，比较依赖语言特性。

Java 的话，无论 ArrayList 还是 LinkedList，addAll 方法的复杂度都是 \(O(N)\)，所以总体的最坏时间复杂度会达到 \(O(N^2)\)，除非你自己实现一个复杂度为 \(O(1)\) 的 addAll 方法，底层用链表是可以做到的，因为多条链表只要简单的指针操作就能连接起来。

当然，最主要的原因还是因为教科书上从来没这么教过...

二叉树题目的通用思考过程

综上，遇到一道二叉树的题目时的通用思考过程是：

  1. 是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现。
  2. 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值。
  3. 无论使用哪一种思维模式，你都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做。

后序位置的特殊之处

中序和前序位置

说后序位置之前，先简单说下中序和前序。

中序位置主要用在 BST 场景中，你完全可以把 BST 的中序遍历认为是遍历有序数组。

前序位置本身其实没有什么特别的性质，之所以你发现好像很多题都是在前序位置写代码，实际上是因为我们习惯把那些对前中后序位置不敏感的代码写在前序位置罢了。

后序位置

你可以发现，前序位置的代码执行是自顶向下的，而后序位置的代码执行是自底向上的：

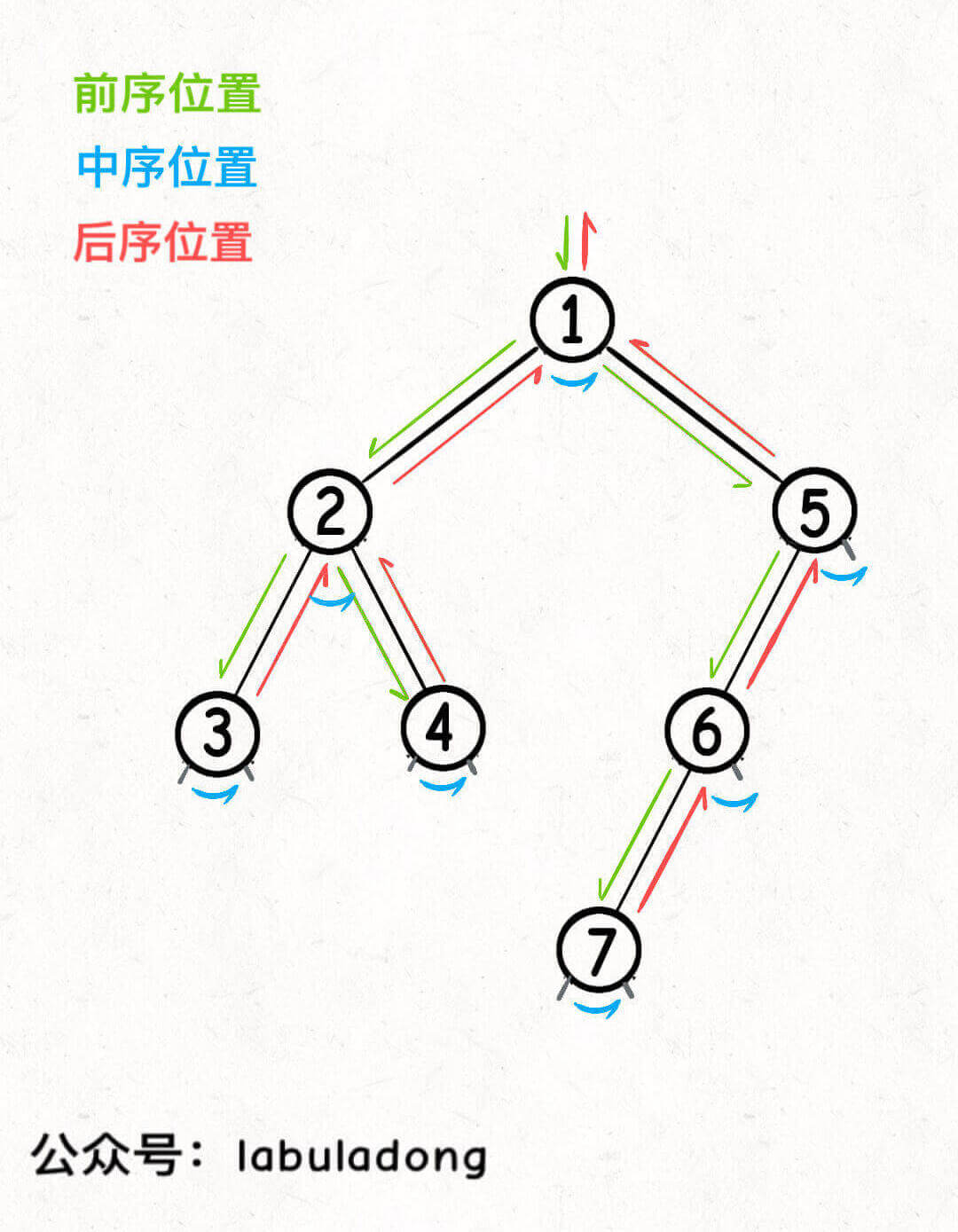
二叉树的前中后序位置

这不奇怪，因为本文开头就说了前序位置是刚刚进入节点时刻，后序位置是即将离开节点的时刻。

但这里面大有玄妙，这意味着前序位置的代码只能从函数参数中获取父节点传递来的数据，而后序位置的代码不仅可以获取参数数据，还可以获取到子树通过函数返回值传递回来的数据。

两个简单问题

举一个具体例子，现在给你一棵二叉树，有两个简单问题：

  1. 如果把根节点看作第 1 层，如何打印出每一个节点所在的层数？
  2. 如何打印出每个节点的左右子树各有多少节点？

解决第一个问题的代码如下：

1
2
3
4
5
6
7
8
9
10
11
// 二叉树遍历函数
void traverse(TreeNode root, int level) {
    if (root == null)
        return;
    // 前序位置
    System.out.printf("节点 %s 在第 %d 层", root, level);
    traverse(root.left, level + 1);
    traverse(root.right, level + 1);
}
// 调用
traverse(root, 1);

解决第二个问题的代码如下：

1
2
3
4
5
6
7
8
9
10
11
// 定义：输入一棵二叉树，返回这棵二叉树的节点总数
int count(TreeNode root) {
    if (root == null)
        return 0;
    int leftCount = count(root.left);
    int rightCount = count(root.right);
    // 后序位置
    System.out.printf("节点 %s 的左子树有 %d 个节点，右子树有 %d 个节点",
            root, leftCount, rightCount);
    return leftCount + rightCount + 1;
}

这两个问题的根本区别在于：一个节点在第几层，你从根节点遍历过来的过程就能顺带记录，用递归函数的参数就能传递下去；而以一个节点为根的整棵子树有多少个节点，你需要遍历完子树之后才能数清楚，然后通过递归函数的返回值拿到答案。

结合这两个简单的问题，可以发现后序位置的特点，只有后序位置才能通过返回值获取子树的信息。

那么换句话说，一旦你发现题目和子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码了。

二叉树的直径

下面看一下力扣第 543 题「二叉树的直径」，计算一棵二叉树的最长直径长度。

所谓二叉树的直径长度，就是任意两个节点之间的路径长度。最长直径并不一定要穿过根节点，比如下面这棵二叉树。

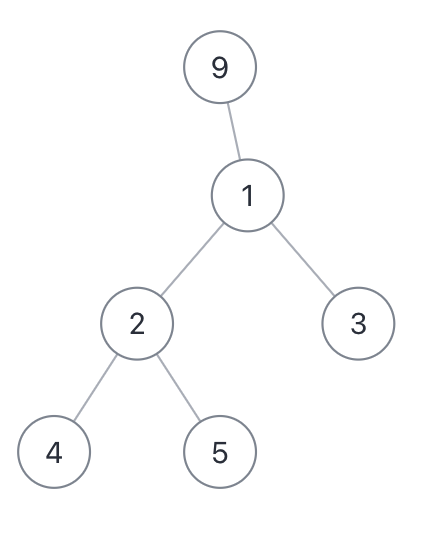
二叉树的直径

它的最长直径是 3，即 [4,2,1,3]，[4,2,1,9] 或者 [5,2,1,3] 这几条直径的长度。

解决这题的关键在于，每一条二叉树的直径长度，就是一个节点的左右子树的最大深度之和。

现在让我求整棵树中的最长直径，那直截了当的思路就是遍历整棵树中的每个节点，然后通过每个节点的左右子树的最大深度算出每个节点的直径，最后把所有直径求个最大值即可。

最大深度的算法已经实现过了，上述思路可以写出如下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    // 记录最大直径的长度
    int maxDiameter = 0;
    
    public int diameterOfBinaryTree(TreeNode root) {
        // 对每个节点计算直径，求最大直径
        traverse(root);
        return maxDiameter;
    }
    
    // 遍历二叉树
    void traverse(TreeNode root) {
        if (root == null)
            return;
        // 对每个节点计算直径
        int leftMax = maxDepth(root.left);
        int rightMax = maxDepth(root.right);
        int myDiameter = leftMax + rightMax;
        // 更新全局最大直径
        maxDiameter = Math.max(maxDiameter, myDiameter);
        
        traverse(root.left);
        traverse(root.right);
    }
    
    // 计算二叉树的最大深度
    int maxDepth(TreeNode root) {
        if (root == null)
            return 0;
        int leftMax = maxDepth(root.left);
        int rightMax = maxDepth(root.right);
        int res = Math.max(leftMax, rightMax) + 1;
        return res;
    }
}

这个解法是正确的，但是运行时间很长，原因也很明显，traverse 遍历每个节点的时候还会调用递归函数 maxDepth，而 maxDepth 是要遍历子树的所有节点的，所以最坏时间复杂度是 \(O(N^2)\)。

这就出现了刚才探讨的情况，前序位置无法获取子树信息，所以只能让每个节点调用 maxDepth 函数去算子树的深度。

那如何优化？

我们应该把计算直径的逻辑放在后序位置，准确说应该是放在 maxDepth 的后序位置，因为 maxDepth 的后序位置是知道左右子树的最大深度的。

优化后的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    // 记录最大直径的长度
    int maxDiameter = 0;
    
    public int diameterOfBinaryTree(TreeNode root) {
        maxDepth(root);
        return maxDiameter;
    }
    
    int maxDepth(TreeNode root) {
        if (root == null)
            return 0;
        int leftMax = maxDepth(root.left);
        int rightMax = maxDepth(root.right);
        // 后序位置，顺便计算最大直径
        int myDiameter = leftMax + rightMax;
        maxDiameter = Math.max(maxDiameter, myDiameter);
        
        return Math.max(leftMax, rightMax) + 1;
    }
}

这次，时间复杂度只有 maxDepth 函数的 \(O(N)\) 了。

讲到这里，照应一下前文：遇到子树问题，首先想到的是给函数设置返回值，然后在后序位置做文章。

请思考一下，运用后序遍历的题目使用的是「遍历」思路还是「分解问题」思路？

使用了「分解问题」的思路。因为当前节点接收并利用了子树返回的信息，这就意味着你把原问题分解成了当前节点 + 左右子树的子问题。

层序遍历

代码框架

二叉树题型主要用来培养递归思维，而层序遍历属于迭代遍历，也比较简单，下面是代码框架：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 定义：输入一棵二叉树的根节点，层序遍历这棵二叉树
void levelTraverse(TreeNode root) {
    if (root == null)
        return;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    
    // 从上到下遍历二叉树的每一层
    while (!q.isEmpty()) {
        int sz = q.size();
        // 从左到右遍历每一层的每个节点
        for (int i = 0; i < sz; i++) {
            TreeNode cur = q.poll();
            // 将下一层节点放入队列
            if (cur.left != null) {
                q.offer(cur.left);
            }
            if (cur.right != null) {
                q.offer(cur.right);
            }
        }
    }
}

这里面的 while 循环和 for 循环分管从上到下和从左到右的遍历：

层序遍历

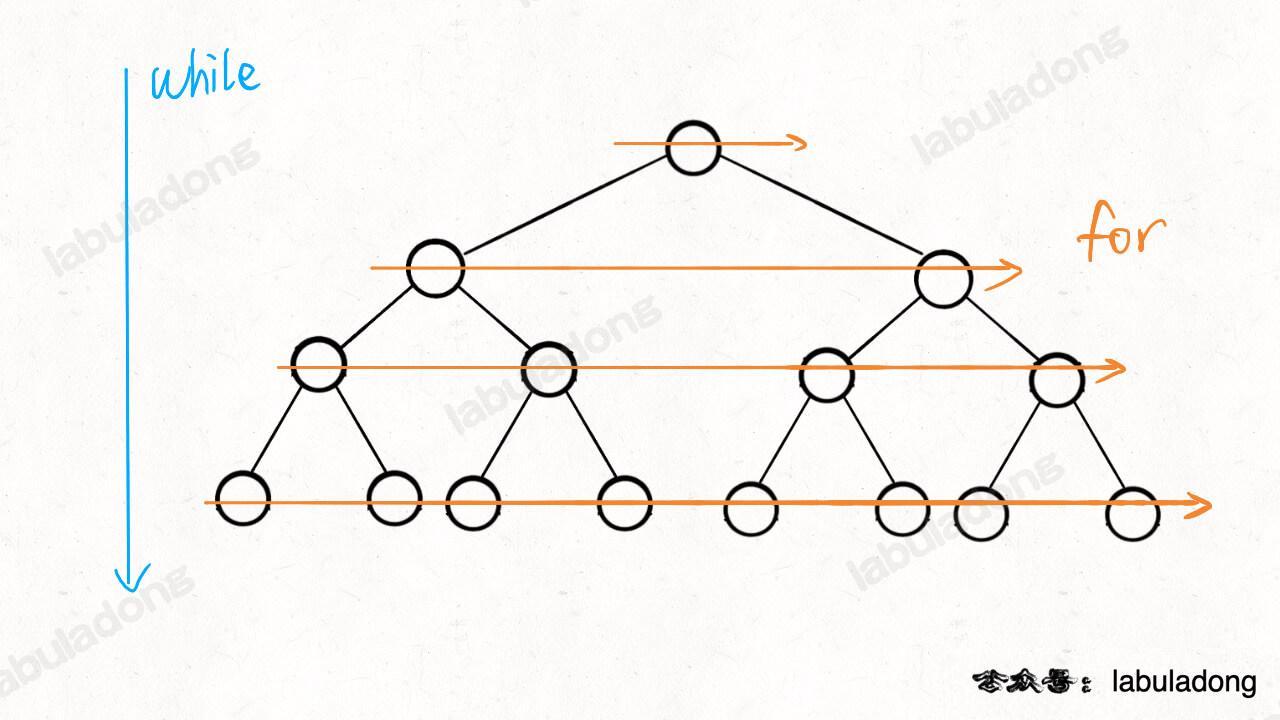
BFS 算法框架就是从二叉树的层序遍历扩展出来的，常用于求无权图的最短路径问题。

当然，这个框架还可以灵活修改，题目不需要记录层数（步数）时，可以去掉上述框架中的 for 循环，比如 Dijkstra 算法中计算加权图的最短路径问题，详细探讨了 BFS 算法的扩展。

值得一提的是，有些很明显需要层序遍历技巧的二叉树的题目，也可以用递归遍历的方式去解决，而且技巧性会更强，非常考察你对前中后序的把控。

比如说：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    List<List<Integer>> res = new ArrayList<>();
    
    List<List<Integer>> levelTraverse(TreeNode root) {
        if (root == null)
            return res;
        // root 视为第 0 层
        traverse(root, 0);
        return res;
    }
    
    void traverse(TreeNode root, int depth) {
        if (root == null)
            return;
        // 前序位置，看看是否已经存储 depth 层的节点了
        if (res.size() <= depth) {
            // 第一次进入 depth 层
            res.add(new ArrayList<>());
        }
        // 前序位置，在 depth 层添加 root 节点的值
        res.get(depth).add(root.val);
        traverse(root.left, depth + 1);
        traverse(root.right, depth + 1);
    }
}

这种思路从结果上说确实可以得到层序遍历结果，但其本质还是二叉树的前序遍历，或者说 DFS 的思路，而不是层序遍历，或者说 BFS 的思路。因为这个解法是依赖前序遍历自顶向下，自左向右的顺序特点得到了正确的结果。

这个解法更像是从左到右的「列序遍历」，而不是自顶向下的「层序遍历」。所以对于计算最小距离的场景，这个解法完全等同于 DFS 算法，没有 BFS 算法的性能的优势。

参考资料

  1. labuladong 的算法小抄
  2. 牛客网
  3. 力扣网