二叉树与递归的框架思维「浓缩版」

发表于 更新于 分类于 ， ， 本文字数： 1.5k 阅读时长 ≈ 6 分钟 阅读次数：

本文是 二叉树与递归的框架思维「详解版」的关键知识总结。

二叉树解题思维分两类：

  1. 是否可以通过遍历一遍二叉树得到答案？

    如果可以，用一个 traverse 函数配合外部变量来实现，这叫 「遍历」的思维模式。

  2. 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？

    如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

无论哪种思维模式，我们都需要思考：

如果单独抽出一个二叉树节点，它需要做什么事情？需要在什么时候（前/中/后序位置）做？其他的节点不用你操心，递归函数会帮你在所有节点上执行相同的操作。

二叉树的所有问题，就是让你在前中后序位置注入巧妙的代码逻辑，去达到自己的目的，你只需要单独思考每一个节点应该做什么，其他的不用你管，抛给二叉树遍历框架，递归会在所有节点上做相同的操作。

二叉树的重要性

  • 快速排序的本质是二叉树的前序遍历。
  • 归并排序的本质是二叉树的后序遍历。

深入理解前中后序

二叉树遍历框架

1
2
3
4
5
6
7
8
9
void traverse(TreeNode root) {
    if (root == null)
        return;
    // 前序位置
    traverse(root.left);
    // 中序位置
    traverse(root.right);
    // 后序位置
}

只要是递归形式的遍历，都可以有前序位置和后序位置，分别在递归之前和递归之后。

前序位置，就是刚进入一个节点（元素）的时候，后序位置就是即将离开一个节点（元素）的时候，你把代码写在不同位置，代码执行的时机也不同：

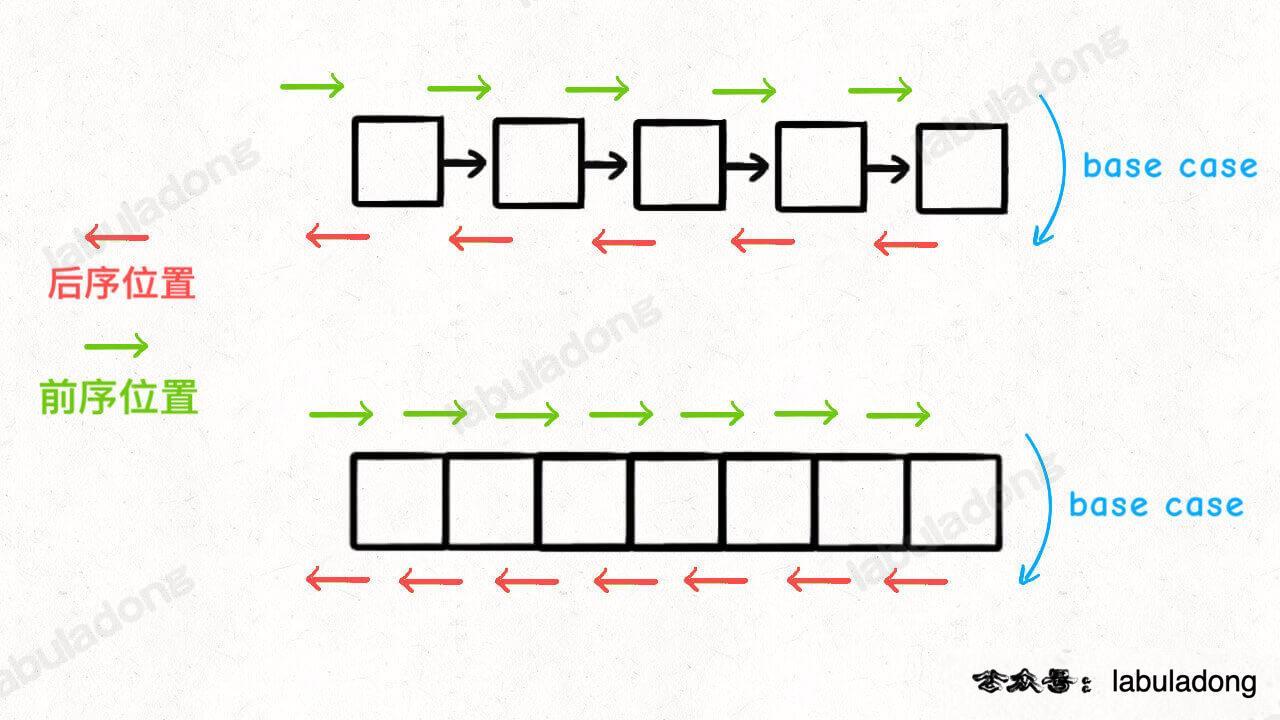
代码执行时机

前中后序位置的特殊性

前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点，绝不仅仅是三个顺序不同的 List。

  • 前序位置的代码在刚刚进入一个二叉树节点的时候执行；
  • 后序位置的代码在将要离开一个二叉树节点的时候执行；
  • 中序位置的代码在一个二叉树节点左子树都遍历完，即将开始遍历右子树的时候执行。

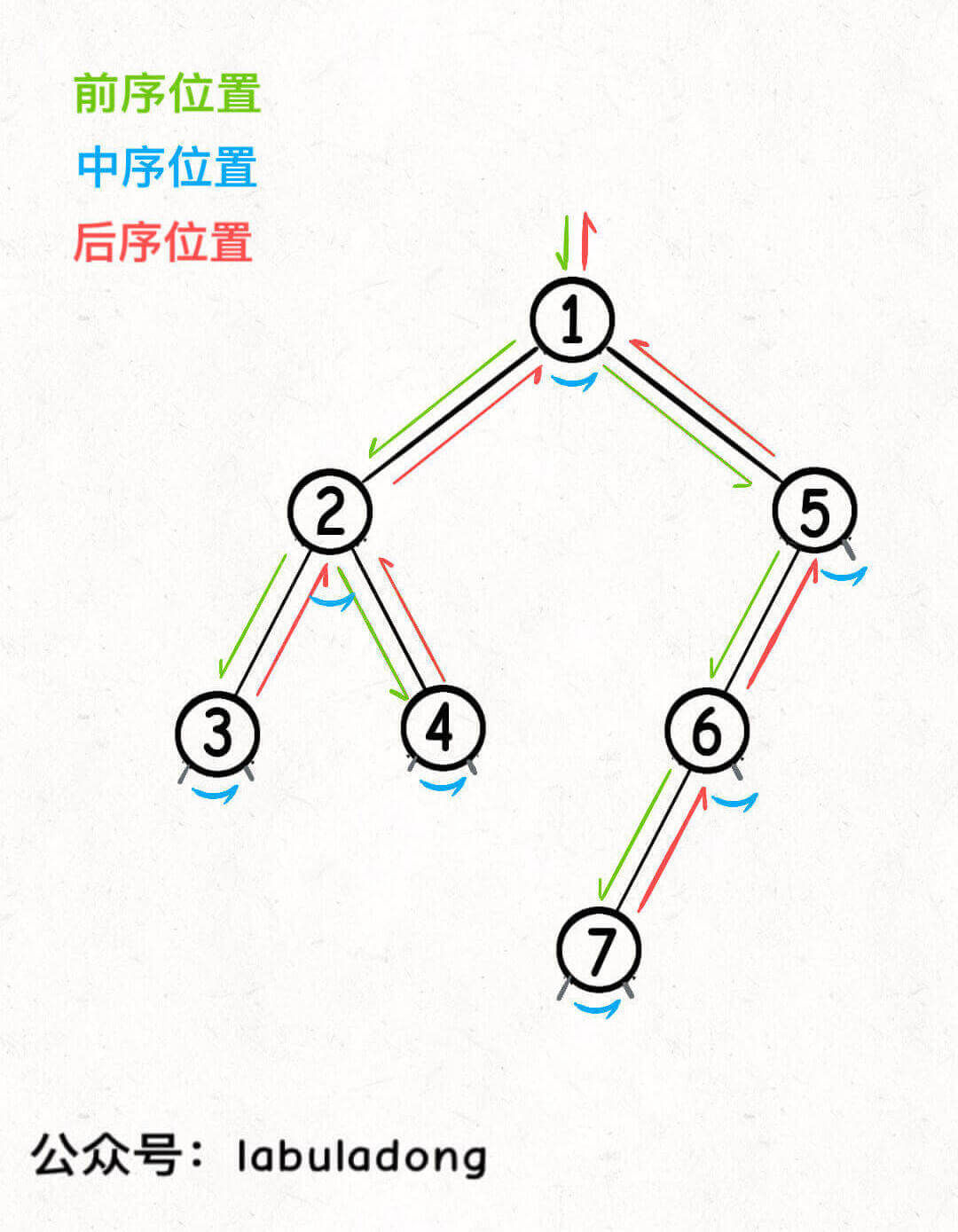
二叉树的前中后序的位置

每个节点都有唯一属于自己的前中后序位置，因此前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点。

这也就是为什么多叉树没有中序位置的原因，多叉树节点没有「唯一」的中序遍历位置。

二叉树的所有问题，就是让你在前中后序位置注入巧妙的代码逻辑，去达到自己的目的，你只需要单独思考每一个节点应该做什么，其他的不用你管，抛给二叉树遍历框架，递归会在所有节点上做相同的操作。

两种解题思路

  1. 是否可以通过遍历一遍二叉树得到答案。如果可以，函数签名一般是 void traverse(...)，没有返回值，靠更新外部变量来计算结果。
  2. 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案。函数名根据该函数具体功能而定，而且一般会有返回值，返回值是子问题的计算结果。
  3. 无论使用哪种思路，都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做。

题目 1：牛客BM28 二叉树的最大深度

题目 2：二叉树的前序遍历

后序位置的特殊之处

中序和前序位置

中序位置主要用在 BST 场景中，完全可以把 BST 的中序遍历认为是遍历有序数组。

前序位置没啥特殊，习惯将对前中后序位置不敏感的代码写在前序位置。

后序位置

前序位置的代码执行是自顶向下的，而后序位置的代码执行是自底向上的。

二叉树的前中后序的位置

这意味着前序位置的代码只能从函数参数中获取父节点传递来的数据，而后序位置的代码不仅可以获取参数数据，还可以获取到子树通过函数返回值传递回来的数据。

题目 1：把根节点看作第 1 层，如何打印出每一个节点所在的层数？

题目 2：如何打印出每个节点的左右子树各有多少节点？

题目 3：力扣第 543 题「二叉树的直径」

层序遍历

代码框架

二叉树题型主要用来培养递归思维，而层序遍历属于迭代遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void levelTraverse(TreeNode root) {
    if (root == null)
        return;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    // 从上到下遍历二叉树每一层
    while(!q.isEmpty()) {
        int sz = q.size();
        // 从左到右遍历每一层的每个节点
        for (int i = 0; i < sz; i++) {
            TreeNode cur = q.poll();
            // 将下一层节点放入队列
            if (cur.left != null)
                q.offer(cur.left);
            if (cur.right != null)
                q.offer(cur.right);
        }
    }
}

层序遍历

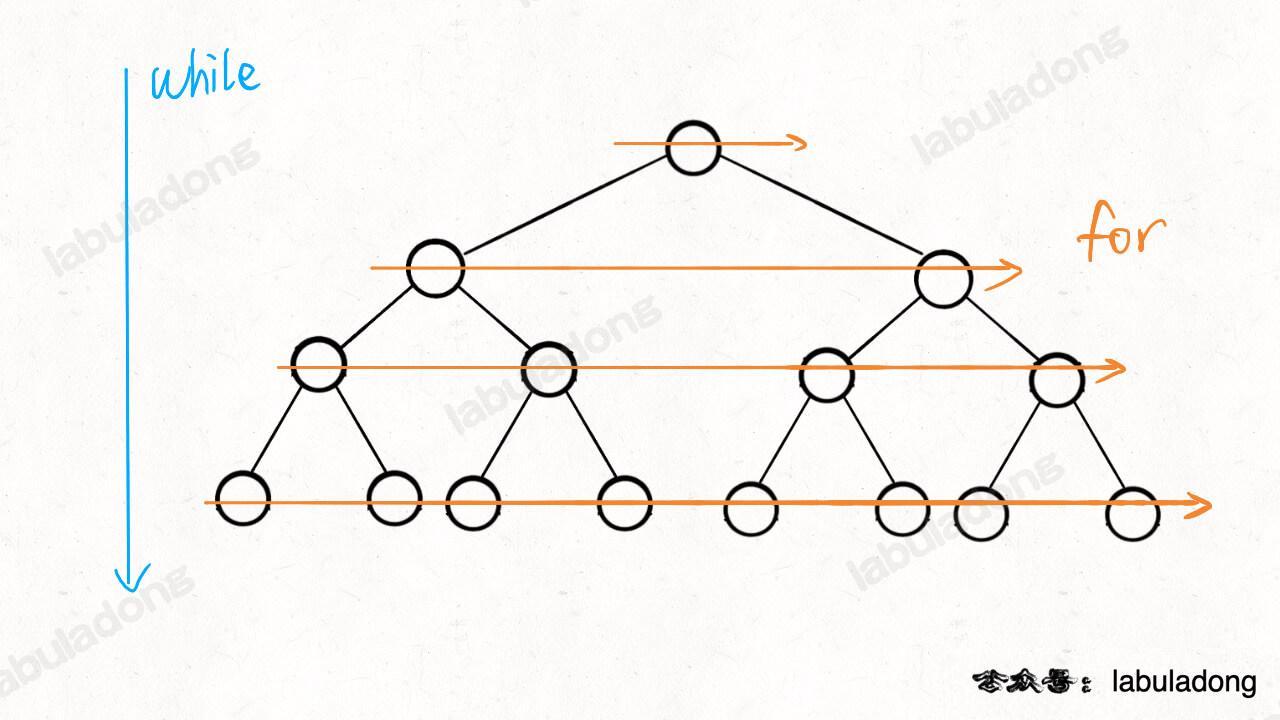
BFS 算法框架就是从二叉树的层序遍历扩展而来，常用于求无权图的最短路径问题。

框架还可以灵活修改，题目不需要记录层数（步数）时，可以去掉上述框架中的 for 循环，比如 Dijkstra 算法中计算加权图的最短路径问题，详细探讨了 BFS 算法的扩展。

参考资料

  1. labuladong 的算法小抄
  2. 牛客网
  3. 力扣网